1.4. Нелинейные законы фильтрации/ввести нумерацию/

Проведенные в дальнейшем эксперименты показали, что закон Дарси не является универсальным и нарушаются области малых и больших скоростей. Нарушение в области малых скоростей связано с молекулярным эффектом. Причины, вызывающие отклонение от закона Дарси при больших скоростях, являются до настоящего времени предметом дискуссии среди исследователей.

В 1901 году австрийский ученый Форхгейме, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости двучленным законом фильтрации:

, (18)

Двучленный закон фильтрации в дифференциальной форме при прямолинейной фильтрации газа в принятых сейчас обозначениях, без учета силы тяжести имеет два вида записи:

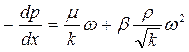, (19)

или

(20)

где b - дополнительная константа пористой среды, определяемая экспериментально,

l – коэффициент макрошероховатости, характеризующий структуру порового пространства, r - плотность газа (жидкости).

Первое слагаемое в правой части уравнения (19) учитывает потери давления вследствие вязкости жидкости, второе слагаемое – инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов.

При малых скоростях течения природа нелинейности закона фильтрации иная, чем в области больших скоростей фильтрации (больших значений числа Рейнольдса). Она связана с проявлением неньютоновских свойств фильтрующихся флюидов, а также других физико-химических эффектов и больших поверхностных сил (сил взаимодействия между флюидом и твердым скелетом). При очень малых скоростях фильтрации неньютоновскими свойствами в пористой среде могут обладать даже ньютоновские жидкости. Но с ростом скорости этот эффект в ньютоновских жидкостях исчезает. В нефтегазовом деле к жидкостям, проявляющим неньютоновские свойства, относят аномальные нефти и буровые растворы. Поэтому для качественного изучения вопроса и количественной оценки этих эффектов необходимо отказаться от модели вязкой однородной жидкости и заменить ее какой-либо другой реологической моделью пластового флюида.

Ограничимся формулировкой наиболее простого нелинейного закона фильтрации неньтоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом. Для случая одномерного линейного потока его можно представить в виде

, при  , (21)

, при  ,

где  - предельный (начальный) градиент давления, по достижении которого начинается движение жидкости: при меньших значениях градиента давления фильтрационное течение отсутствует, этот параметр измеряется в лабораторных условиях. зависит от начального сдвига жидкости и эффективного диаметра капилляра.

Закон фильтрации записывают также в виде одночленной степенной формулы:

 (22)

где С и n - постоянные, определяемые опытным путем, причем 1< n < 2.

При n = 1 из (22) получается закон Дарси, при n = 2 – квадратичный закон А.А. Краснопольского.

Таким образом, формула (19) имеет два параметра b и k, которые подлежат дальнейшему изучению и установлению связи между ними.

Входящий в линейный закон фильтрации Дарси (17) коэффициент проницаемости определяется при исследовании кернов или на основе гидродинамических исследований.

Исследованиями показано, что для пористых сред коэффициент проницаемости зависти от размера зерен и их дисперсности, коэффициента пористости, формы зерен, степени их сцементированности и. т. д.

Л.С. Лейбензон предложил выразить коэффициент проницаемости в виде:

(23)

где d – линейный размер (диаметр) зерен пористой среды, Sl – безразмерный критерий (число Слихтера), зависящий от коэффициента пористости и структуры порового пространства, т. е.

(24)

где e - некоторый параметр, характеризующий структуру порового пространства пласта, m – коэффициент пористости.

 

В связи с тем, что линейный закон фильтрации Дарси всё-таки является приближенным законом, при увеличении скорости фильтрации жидкости и соответствующем увеличении скоростного напора сделанное ранее при выводе линейного закона фильтрации допущение может оказаться несправедливым, тогда и возникнут погрешности в расчетах. В этих случаях говорят, что линейный закон фильтрации (закон Дарси) имеет верхнюю и нижнюю границы применения.

Верхняя границаопределяется группой причин связанных с проявлением инерционных сил при высоких скоростях фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением Re_крчисла Рейнольдса:

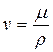,  , (25)

где d– линейный размер пористой среды,

v– кинематический коэффициент вязкости флюида.

В таких случаях принято говорить о так называемых нелинейных законах фильтрации, например выражения (18 – 20).

Первая количественная оценка верхней границы применимости закона Дарси была выполнена Павловским, который, опираясь на результаты Слихтера, полученные для модели идеального грунта, и полагая характерный размер dравный эффективному диаметру d_эфвывел следующую формулу для числа Рейнольдса:

, (26)

Использовав эту формулу и данные экспериментов, Н.Н. Павловский установи, что критическое значение числа Рейнольдса находится в пределах

Достаточно узкий диапазон изменения значений Re_кробъясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.

Для удобства обработки результатов многочисленных экспериментов различных авторов В.Н.Щелкачев предложил использовать безразмерный параметр, названный им параметром Дарси

. (27)

Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Из выражения (17) следует, что если параметр Дарси равен единицы

, (28)

то закон Дарси справедлив.

Таким образом, равенство (28) должно выполняться при Re< Re_кр. Данный параметр упрощает исследование границы применимости линейного закона фильтрации.

Таблица 1.

Интервалы критических значений Reдля различных образцов пористых сред

Образец пористой среды	Диапазон критических значений
Однородная дробь	13-14
Однородный крупнозернистый песок	3-10
Неоднородный мелкозернистый песок с преобладанием фракций диаметром менее 0,1 мм	0,34-0,24
Сцементированный песчаник	0,05-1,4

 

Однако вследствие различной структуры и состава пористых сред получить универсальную зависимость не удается.

Нижняя границаопределяется проявлением неньютоновских реологических свойств жидкости, ее взаимодействия с твердым скелетом пористой среды при достаточно малых скоростях фильтрации (например, выражение 21).

Задачи из Басниева.

 

1. При фильтрации жидкости с постоянным расходом через несцементированную пористую среду произошло вымывание мелких фракций песка. Изменилась ли при этом скорость фильтрации и средняя скорость движения жидкости?

 

2. Куб с ребром 1 м наполнили шарами диаметром 10 см каждый, а куб с ребром 1 см точно так же уложили шарами диаметром 1 мм каждый. Пористость какой засыпки больше?

 

3. Показать, что если образец пористого материала, имеющий объем Vи пористость m, разбить на nчастей объемом V_i(i = 1, …, n), то  , где m_i- пористость i-й части. Рассмотреть также случай, когда все V_iодинаковы.

 

4. Определите пористость фиктивного грунта, сложенного шарами диаметром D, центры которых находятся в вершинах кубической решетки с периодом D.

Ответ: 1 – π/6 =0,476.

 

5. Определить удельную поверхность фиктивного грунта, пористость которого m= 0,25 и диаметр шаров 0,2 мм. Найти число шаров в 1 м³.

 

6. Определить пористость, удельную поверхность и просветность для рыхлой кубической упаковки шаров.

 

7. Определить пористость для кубической и гексагональной упаковок шаров.

 

8. Определить коэффициент проницаемости пористой среды (в м² и Дарси), если известно, что коэффициент фильтрации k_ф= 0,3·10 ^{– 4} см/с, кинематический коэффициент вязкости жидкости ν = 10 ^{– 6} м²/с.

 

9. Определить проницаемость при фильтрации через образец площадью 1 см², при перепаде давления 1 кгс/см² с расходом жидкости 1 см³/с, если длина образца 1 см, а фильтрующая жидкость имеет динамический коэффициент вязкости 1 сП (один сантипуаз).

Решение. Из формулы (1.9)  .

Переведем все размерности в СИ:

площадь 1 см² = 10 ^{– 4} м², давление 1 кгс/см² = 98 кПА, расход 1 см³/с = 10^-6 м³/с, длина 1 см = 10^-2 м, вязкость 1 сП = 0,01 П (Пуаз) = 0,001 Па·с =1 мПа·с

м² = 1Д (Дарси) ≈ 1 мкм².

10. Определить коэффициент фильтрации для керна, помещенного под углом α к горизонту, если массовый расход жидкости равен Q_м, плотность жидкости ρ и вязкость μ, разница напоров в начале и конце керна составляет ΔН, площадь сечения S, длина керна L.

 

11. Образец пористой среды длиной 10 см и диаметром 5 см после насыщения под вакуумом керосином с плотностью 810 кг/м³ стал тяжелее на 20 г. Определить коэффициент пористости образца.

 

 

Щелкачев стр. 80

Оценить влияние размеров поверхностей поровых каналов на величину сил сопротивления, определить суммарную поверхность песчинок, заключенных в 1 м³ песчаного пласта. Примем форму песчинок шарообразной, диаметр их одинаковым и обозначим: N - число песчинок в 1 м³ пласта; r- радиус песчинки; поверхность песчинки  ; объем песчинки /в формуле ω/  ; пористость пласта m.

Тогда , V₁ – весь объем шаров,V₂– объем породы.

Суммарная поверхность Sпесчинок, заключенных в 1 м³ песчаного пласта, равна:

 

σ – нет расшиф.