
- •К вопросу удельной энергоемкости маховичных накопителей энергии Berezhnoi d.V.
- •420008 Kazan, Russia
- •Abstract
- •1. Введение
- •2. Оценка потенциальной и кинетической энергии, накопленной диском при вращении его вокруг оси
- •2.1. Общие соотношения
- •2.2. Диск с отверстием
- •2.3. Сплошной диск
- •2.4. Диск равного сопротивления
- •3. Результаты расчета
- •4. Анализ результатов
- •5. Заключение
- •6. Приложение
Applied Mathematical Sciences, Vol. x, 20xx, no. xx, xxx - xxx
К вопросу удельной энергоемкости маховичных накопителей энергии Berezhnoi d.V.
Kazan federal university
420008 Kazan, Russia
berezhnoi.dmitri@mail.ru
Abstract
В работе излагаются основы методики численного исследования удельной энергоемкости маховичных накопителей энергии. В дополнение к традиционной оценке энергоемкости по кинетической энергии добавляется оценка по удельной потенциальной энергии упругих деформаций. Анализируются возможности использования различных конструкционных материалов при изготовлении маховиков, даются некоторые рекомендации по форме маховика. Отмечается, что используемая в работе «расширенная» оценка энергоемкости дает большую вариативность при конструировании маховичных накопителей энергии и в некоторых случаях позволяет снизить скорость вращения роторной части конструкции.
Keywords: маховик, удельная энергоемкость, кинетическая и потенциальная энергия.
1. Введение
В связи с развитием современных технологий в промышленности и на транспорте появляется множество мобильных устройств, поэтому большое значение приобретает проблема аккумулирования энергии. Создание новых материалов позволяет не только совершенствовать уже имеющиеся традиционные электрохимические батареи, а искать новые методы накопления и хранения энергии, в том числе и механические [1-3]. К ним можно отнести так называемые статические и динамические механические накопители энергии.
У статических аккумуляторов механической энергии упругий элемент работает либо на растяжение (сжатие) – что предпочтительнее, либо на кручение (сдвиг), либо на изгиб, но такие аккумуляторы характеризует сравнительно небольшая накопляемая удельная энергия. Однако, обладая достаточно ценными свойствами – стабильностью накопления энергии, высоким КПД, долговечностью, они обеспечили себе прочное место во многих машинах и механизмах.
Одной из относительно простых и, в то же время, крайне перспективных является технология накопления энергии при помощи маховика. Маховик сохраняет переданную ему энергию в виде кинетической энергии вращения. Другими словами, это некое массивное тело вращения, использующееся в качестве накопителя (инерционный аккумулятор) кинетической энергии [4]. Однако даже современные технологии не исчерпывают всех возможностей маховика. При достаточно быстром вращении он может накапливать кинетическую энергию, которую легко не только наращивать, но и использовать, превратив маховик в электромеханический аккумулятор.
В данной работе представлены некоторые результаты оценки накопляемой маховиком энергии, в том числе кинетической и потенциальной энергии деформации, для различных материалов и дан ряд рекомендаций по выбору материалов, из которых можно изготовлять маховик.
2. Оценка потенциальной и кинетической энергии, накопленной диском при вращении его вокруг оси
2.1. Общие соотношения
Рассмотрим
задачу об определении напряжений во
вращающемся с постоянной угловой
скоростью
 однородном диске плотностью
однородном диске плотностью
 [5]. В этом случае полученное решение не
зависит от угла вращения
[5]. В этом случае полученное решение не
зависит от угла вращения
 ,
а зависит только от текущего радиуса
,
а зависит только от текущего радиуса
 диска. Известно, что на каждую точку
вращающегося тела действует центробежная
сила, пропорциональная расстоянию от
оси вращения, поэтому радиальная
составляющая потенциала массовых сил
имеет вид
диска. Известно, что на каждую точку
вращающегося тела действует центробежная
сила, пропорциональная расстоянию от
оси вращения, поэтому радиальная
составляющая потенциала массовых сил
имеет вид
 ,
а уравнения равновесия записываются в
виде
,
а уравнения равновесия записываются в
виде
 ,
,
где
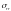 - радиальное напряжение,
- радиальное напряжение,
 - окружное. Зависимости между компонентами
тензора деформации и компонентами
вектора перемещения в полярных координатах
записываются в следующем виде:
- окружное. Зависимости между компонентами
тензора деформации и компонентами
вектора перемещения в полярных координатах
записываются в следующем виде:

откуда

т.к.

Представим зависимости между напряжениями и деформациями в соответствии с обобщенным законом Гука. Применительно к плоскому напряженному состоянию эти соотношения можно записать в виде
 (1)
(1)
где
 - коэффициент Пуассона,
- коэффициент Пуассона,
 - модуль Юнга материала диска.
- модуль Юнга материала диска.
П одставим
эти соотношения в уравнение равновесия:
одставим
эти соотношения в уравнение равновесия:
Получим его в перемещениях:
 (2)
(2)
Известно,
что общее решение уравнения (2) можно
представить как сумму решений однородного
уравнения
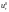 и частного решения
и частного решения
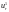 неоднородного.
неоднородного.
Общее
решение однородного уравнения будем
искать в виде
 .
Подставляя это выражение в однородное
уравнение равновесия,
.
Подставляя это выражение в однородное
уравнение равновесия,

Получим
 .
.
Значит
 и
и
 ,
,
где
константы
 и
и
 подлежат определению из граничных
условий. Частное решение неоднородного
уравнения будем искать в виде
подлежат определению из граничных
условий. Частное решение неоднородного
уравнения будем искать в виде
 .
.
Подставляя это выражение в (2), получим
 ,
,
откуда
 .
.
Таким образом, решение уравнения (2) имеет вид
 ,
(3)
,
(3)
Найдем соотношения для напряжений, для этого уравнение (3) подставляем в найденные выражения для :

Получаем, что

Далее находим :

Отсюда,

Потенциальная энергия деформации определяется в виде

