
Шпора по физике 2006 (Суриков, ИВТ-2XX)
.doc|
1. Электрическое поле. Хар-ки электрического поля. Материальным носителем поля явл электромагнитные волны или фотоны. Взаимодействие Эл зарядов осущ ч/з обмен фотонами. Для эл поля используют следующие хар-ки: Силовую (напряженность) и энергетическую (потенциал). Напряженность поля - вектор, которого определяет силовое действие электронов поля на эл заряды и численно = кулоновской силе, которая действует на еденицу положительного заряда помещенного в данную (.). Вектор напр направлен в сторону действия кулоновской силы. Потенциал – это энергетическая хар-ка, численно = потенциальной энергии, которой обладает единичный положительный заряд, помещенный в данную (.) поля. А=q(φ1-φ2) – работа кулоновской силы. φ=∑ni=1φi На эл поле вып принцип суперпозиции т.е. каждый заряд создает эл поле не зависимо от др зарядов в пространстве. E=-dφ/dr – связь напряженности с потенциалом. |
2.Теорема Гаусса Т: Поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов делённой на 0 . Пусть электростатическое поле создается зарядом q . Мысленно охватим заряд произвольной поверхностью. Рассчитаем поток вектора напряженности через выбранную замкнутую поверхность.
Для
системы зарядов
Под действием сил электрического поля любой заряд, внесенный в поле будет перемещаться по некоторой линии. Такие линии называются линиями напряженности – линии, в каждой точке которой вектор напряженности совпадает в направлением касательной проведенной к этой линии. За направление силовой линии принято такое направление, по которому стал бы двигаться положительный заряд, внесенный в поле. Электрические силовые линии начинаются у положительного заряда и заканчиваются у отрицательного или же могут уходить в бесконечность. Две силовые линии поля никогда не пересекаются. Плотность линий напряженности пропорциональна величине напряженности в каждой точке. |
|
4. Потенциальная энергия эл.поля. Потенциал эл.поля в данной точке характеризует энергетическое состояние поля в данной точке и равен потенциальной энергии которой обладает единичный точечный заряд помещенный в данную точку поля. Потенциал является однозначной и непрерывной функцией координат определенной с точностью до произвольной постоянной, значение которой зависит от выбора нулевого уровня потенциала. Потенциальная энергия заряда Q0 в поле заряда Q на расстоянии r (*)
Разность потенциалов двух точек равна работе при перемещении единичного положительного заряда из точки 1 в точку 2:
|
6. Связь напряженности и потенциала. Работа
по перемещению единичного положительного
заряда вдоль оси Х равна
|
|
7,8.Поляризация диэлектриков. Диполем называется система двух одинаковых по величине разноимённых точечных зарядов, расстояние между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Молекулы атомы или диэлектрики которые в отсутствие внешнего поля не имеют дипольного момента называются неполярными, молекулы обладающие дипольным моментом в отсутствие внешнего поля называют полярными. Вектор
поляризации
определяется
как дипольный момент единицы объёма
диэлектрика.
где -диэлектрическая восприимчивость. Полярные диэлектрики
Неполярные диэлектрики
|
11. Электроемкость, конденсатор. Электроемкость – это способность проводника накапливать эл заряды. Электроемкостью наз-ся вел-на, показывающая какой заряд надо поместить на поверхность проводника, чтобы его заряд изменился на 1. C=q/φ . φ=q/(4πε0εr) → C=4πε0εr (ед изм – [Ф] фарад) Любая система проводников, используемый для накопления эл зарядов наз-ся конденсатором. С=(Е0ЕS)/d – электроемкость конденсатора. Сферический конденсатор: C=(4πε0ε)/ln(R1/R2)
|
|
15. Возникновение ЭДС индукции. Появление разности потенциалов на концах проводника обусловлено разделением зарядов под действием силы Лоренца. Разность потенциалов играет роль источника тока, если концы проводника замкнуть сопротивлением. В этом случае по цепи будет протекать постоянный ток, получивший название ЭДС. Е=∆φ Е=BlU. Эта ЭДС по своей сути явл ЭДС индукции Е=ЕИНД. Причина возникновения ЭДС индукции в проводнике – изменение магнитного потока явл разделением зарядов в проводнике под действием силы Лоренца. Вычисление ЭДС индукции: 1. При перемещении проводника в м.п. Е=BlUcosβ. 2. Во вращающемся контуре в м.п. E=BSωsin(ωt+α)
|
16. ЭДС. Закон Ома для неоднородного участка цепи. Для того чтобы ток не прекращался (+) заряды нужно отрывать от (-) заряженного тела и переносить на (+) заряженное тело. Сторонние силы – это силы не электростатической природы, разделяющие заряды разных знаков. Природа сторонних сил зависит от того, какой источник тока вкл в сеть. Источник тока – это устройство в котором действуют сторонние силы. В источнике тока электростатические силы совершают (-) работу, а их работа во всей цепи = 0. ЭДС – это скалярная величина = работе сторонних сил по перемещению единичного заряда в замкнутой цепи. Е=Аст/q (ед изм [1B]).Неоднородным наз участок цепи, содержащий источник тока. На неоднородный уч цепи действуют и электростатические силы и сторонние силы. •════███═══╡╞══• ток может течь в любую сторону за время dt работа => dA=dAk+dAct 1 I → R E 2 Заряд, переносимый за время dt => ∆ φ12dq+Edq
dA=dQ;
dQ=I2Rdt;
I2Rdt=∆
φ12dq+Edq
U=∆ φ12+E – напряжение в этой ф-ле. Знак ЭДС берется (+) если она создает ток, совпадающий с током на этом участке. Закон
Ома для полной цепи:
|
|
17,18,19. Закон Ома и Джоуля-Ленца в классической электрон теории Ме. Электросопр Ме обусловлено столк-м электронов с атомами кристал решетки. Fкул=еЕ <>- сред Длина своб пробега электронов. <u>=Umax/2 j=en<u> Напр-ть Е эл тока внутри Ме, обус-я созд-м разности потенц-в на концах Ме. <u>=Umax/2=a×<>/2, <>-сред время своб пробега. <>=<>/(<>+<u>) u=0 т.к.на 8 поряд.меньше v. <u>=а/2*<>/<>=Fk×<>/2m<>= =Ee<l>/2m<>, j=en<u>=ne2<>E/2m<>, s=ne2<l>/2m<>=1/ s- эл-провод-ть - уд эл/сопрот-е j=1/*E При столкновении выд-ся тепло: mU2max/2*n*(1/<>)=- объем.плотность энергии-кол-во энергии, кот выд-ся в единице V при столкно-вении своб электронов с ат.кр. реш-ки в 1с. =me2E2<l>2/2m2<>2 n1/(<l>/<>)= ne2<>E2/2m<>=sE2
|
20. Закон Видемана-Франца. Недост клас электрон теор. Отношение коэф удель теплопров-ти к коэф уд эл-ти для всех металлов есть величина пост и зав только от темп-ы. æ=1/3*<><>’cv ’- пл-ть ид газа cv- молярн теплоём. cv=3R/2 (cv)æ=cv/=3R/2= 3kNA/2mNA=3k/2m ’=mn æ/=<><>mn3k2m<>/3*2mne2<>=km<>2/e2 <>2/2=3/2*kT æ/=km<>22/e22=3/2*k22T/e2 æ/=3(k/e)2T k-пост Больцмана. 1) Клас электрон теор объясняет эл/св-ва Ме 2) Тепловые и эл/св-ва объяс-с Но (недостатки) 1)экспет <<теорит 2)=2m<>/ne2<>= | <>2/2=3/2*kT <>T | -> T ( среш=3R сэлектр=3R/2 сдиэл=среш=3R сМе= среш+сэлектр=4,5R (сМе)теор=1,5(сдиэл)теор экспер сМесдиэл=25 Дж/моль*К
|
|
27. Магнитное поле движущегося заряда и элемента тока:Выделим в ф-ле магнитн. взаим-я зарядов величины,связанные с первым зарядом: B21=μ0q1/4πr12^3* [v1r12] тогда магнитн.силу,действ-ую на 2-ой заряд можно записать: F21=q2[v2B21] мы получили силу Лоренца,действующую на q2 со стороны q1.B21-вектор индукции магнитного поля,созданного зарядом q1 в точке,где в данное мгновение находится q2 (рис) dB=μ0dq/4πr^3* [vr]-инд-я магн.поля движ.заряда dB=μ0dqsinα/4πr^2 Линии индукции могнитн.поля:Магнитн. поле графически изображают с пом.линий индукции.Их проводят так,что касательные к ним в каждой точке совпадают с вектором индукции магнитн.поля.Линии инд.магнитн. поля замкнутые.Это отражает вихревой хар-ер магн.поля.
|
28. Расчет магнитн.поля прямого проводника с током:
П
|
|
29. Теор о цирк-и вект инд магн поля В. BdL- эл-т длины произ замк конт L. LBdL – цирк-я вектора В по замк конт L. Пуст имеется проводник с током (ток напр на нас) (РИС) BdL=BdLcos dL=dLcos dL=rd LBdL=02Brd=02 (0I/2r* rd)=0I/2*2=0I LBdL=0I (1,n) Цирк-я вектора магн инд по люб замк контуру равна магн пост на алг сумму токов провод-ти, охв-х этим контуром. |
30. Магнитное поле кругового тока:
d
|
|
31,32. Магн поле соленоида и тороида.
Считаем цирк-ю по каждой стороне:
1 3BdL=? Вне соленоида S Bчисло линий В/S0 3BdL=0 Внутри соленоида 2+4=90 cos2+cos4=0 Вне соленоида В2=В40 2=4=0
П
N- число витков кот охват выбр контур. BL=0NI B=0N/L*I=0nI n- число витков приход на ед длины соленоида. Расчет более точен, если (РИС) Д<<длины соленоида. B0=0nI/2*(cos1-cos2)
Т
B
|
33. Магн поле в вещ. Магнетики. Все вещ помещ в магн поле так или иначе реаг на это и поэтому наз магнетиками. Внутри каждого магнетика возн-т собств магн поле (внутр) с индB’. ЕслиB0 -инд внеш магн поля, то магн поле в магнетикеB=B0+B’.B’B0 B’<<B0 парамагнетик.B’B0 B’<<B0-де-ки. B’>>B0- фер-ки. Инт-ть намаг мат-ла харак вектором намаг-яj – величина харак-я намаг-ть мат-а и численно равная, магнитному моменту ед-цы объема магнетика. Изотроп магнетик: j=VPm/V. Анизатр: j=dPm/dV
|
|
3
-
-
|
35. Магнитное поле движущегося заряда и элемента тока. Магнитное поле возникает в пространстве, окружающем намагниченные тела.
Два
точечных заряда, неподвижных друг
относительно друга, взаимодействуют
в соответствии с законом Кулона
Выделим
в ф-ле магн взаимодействия величины,
связанные с первым зарядом
Магнитную силу можно записать в виде F21=q1[V2B21] – сила Лоренца. В21 – вектор индукции м.п.
|
|
35. Магнитное поле движущегося заряда и элемента тока. Магнитное поле возникает в пространстве, окружающем намагниченные тела.
Два
точечных заряда, неподвижных друг
относительно друга, взаимодействуют
в соответствии с законом Кулона
Выделим
в ф-ле магн взаимодействия величины,
связанные с первым зарядом
Магнитную силу можно записать в виде F21=q1[V2B21] – сила Лоренца. В21 – вектор индукции м.п.
|
iмикро=q iмикро- созд магн момент Pm= iмикроS=qs=qr2 fл=qH Сила Лоренца вып-ет роль центрост-й силы: fk=m2/2 a=2/r= =2r2/r=2r2 =2 a=422r fk=m422r
fл=qH
H=0
fk=m2r
H0
fk-fл=m(+)2r
m2r-
qH=m2r+2mr+m()2r
()2<<
qH=2mr
=r -qrH=2mr =-qH/2m – изм-е частоты вращ при вкл магн поля (частота умень – вращ электрона вокруг ядра) Pm=qr2 =/2 Pm=qr2/2=qr2/2 Pm=qr2/2 (Pm- ум-ся) Pm=q2r2H/4m (знак минус не пишем). P’m=Pm n- конц-я j=Pmn= q2r2 nH/4m Н- напр-ть =j/H=q2 nr2/4m
М F=PmdH/dl - эта сила выт-ет образец из магн поля. =-1/4 - пред-я геомагн-я восприим-ть. |
|
37. Рамки с током в магн поле. На кажд сторону будет дейст FA: привило левой руки. Силы дей-е на стороны компен др др.Fb- созд вращ-й момент. Выб ось вращ 00. М- момент силы. M=Fbh h-плечо силы Fb. H=asin Fb=Ibb M=IBbasin Pm=IS M=PmBsin M=[PmB] dA=Md - элем раб. dW=dA –изм энерг магн поля. DW=Md=PmBsin*d W=PmBsin*d=-PmBcos+c =90 c=0 W=-PmBcos. cos=1 =0 – полож устой-го равнов PmВ Wmin. Если Wmax- неуст равнов. cos=1 =180PmВ. |
3 хаотично, и сум-я намаг-ть =0.
Р
<cos>=2nPm2/3kT (зав-т от темп-ы Т) >0 =1+>1 =c/T c- пост-я Кюри.
|
|
39. Ферромагнетики. Домен- обл спант-го намагнич феромагн-ка. Домен имеет макс магн момент. Каждый домен намагничен до насыщ-я У фер-в магн прон-ть не явл пост вел-й, поэтому инд магн поля В сложным образом зависит от напр-ти поля Н. Отст-е инд поля от напр-ти при размаг-и наз магнитным гистерезисом, а замк крив петлёй гистерезиса. (РИС) QO-Hкоэр (коэрцитивная сила) Напр-ть внеш поля, необ-я 4 восст-я первон сост фер-ка.
|
40. Явл-е электро инд. В 1836 Фарадей обнаружил, если замк проводящий контур прониц-т изм-ся магн поток то в контуре возн эл-й ток (инд-й ток) H=const B=0H Ф=BS cos |i|=dФ/dt=d(BS cos)/dt i=-dФ/dt (уст-л Ленц). Своим дейст-м инд-й ток противод причине вызв-й его появ-е. =NФ - потокосц-е N- сичло послед соед проводящих конт-в. i=-d/dt (РИС) Fл=qB qB=qE Fл уравнов-ся Fк Е=B Роль сторон-х сил вып-т Fл, след Ест=Е=B (стор сил)
|
|
4
|
42. Токи при замыкании и размыкании цепи: Вследствие правила Лоренца токи самоинд-ии в контуре направлены так,что исчезновение или появление тока в цепи будет происходить не мгновенно.Цепь:(рис)когда ключ находится в положении (1),в цепи протекает ток I0=ε/R(R-полное сопротивление;L-индуктивность) при (1)→(2) появляется εS=iR; εS=-Ldi/dt; di/i=-Rdt/L; ln(i)=-Rt/L+ln(const); i=const *e^(-Rt/L); L/R=τ-постоянная эл.цепи; t=0; I0=const *e^(-0/τ);i= I0e^(-t/τ); τ-время в течении которого ток изменится в е раз.
|
|
43. Гармонические колебания. Колебания – это повторяющиеся во времени движения. гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса). Если движения повторяются полностью ч/з один и тот же промежуток время, то они наз периодическими, а этот промежуток – периодом. Вел, обратная периоду – частота V=1/T. Циклическая частота W=2πV=рад/с.
А – амплитуда (максимальное смещение), Х – смещение, φ(фаза кол)=W0t+ φ0
|
44. Математический маятник.
И
|
|
45.Физический маятник- нек-ое реальное тело,кот М совершать колебания относит т.закрепления. М за доску, ω-на нас, Lпр-приведенное раст от т.закреп до т.прилож.силы M=mgLпрsinφ, M=-Jφ''; J(ай) Jφ''=mgLпрsinφ, sinφ≈φ, Jφ''+mgLпрφ=0; ωo2=mgLпр/J; ωo=√…;0=(1/2π)√mgLпр/J; T=2π√J/(mgLпр); (L'=J/mLпр)
|
46. Графическое представление колебаний. Сложение колебаний одного направления.
X=a0cosα
(t=0)
Сложение колебаний: Результирующее колебание представляет из себя сумму двух
колебаний:
|
|
47. Сложение взаимно перпендикулярных колебаний.
при
α=0
|
48. Затухающие колебания.
При
затухающих колебаниях энергия системы
не восполняется. На колеблющееся тело
действуют силы сопротивления FC=-rV
Уравнение
затухающих колебаний:
Β=r/2m – коэффициент затухания, а – коэффициент сопротивления.
Инкремент затухания (1) Логарифмический инкремент (2)
Добротность колебательного контура Q=KNC, добротность пропорциональна числу колебаний в колебательной системе за время, в которое амплитуда уменьшится в «е» - раз.
|
|
49. Явление резонанса. Вынужденные колебания. Вынужденные колебания происходят под действием внешней силы. Внешняя сила совершают работу, пополняя запасы энергии колебательной системы. В ней действует сила: F=-Kx, Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к резонансной частоте.
Резонансная
частота – это частота, при которой
амплитуда колебаний достигает своего
максимума. Резонансная частота -
ω0 – собственная циклическая частота. Β – коэффициент затухания.
|
50. Электрический колебательный контур. Колебательный контур состоит из конденсатора, катушки индуктивности, источника ЭДС и сопротивления включенных между собой последовательно. В нем поддерживается длительное переменное движение зарядов и токов, т.е. в нем возникают колебательные процессы..
Q
–заряд на обкладке конденсатора, U
– напряжение на конденсаторе, I=-dQ/dt
U=ε+JR
Дифференциальное уравнение изменения заряда в контре:
|
|
51. Волны общее предст-е. Процесс расспр колеб в упругой среде наз волновым процессом или волной. Если напр колеб совпад с напр расспр волны то волна наз продольной. Если напр колеб волне – поперечная. Геом-е место точек кот достигло колеб в дан момент врем наз фронтом. Геом место точек колеб-ся в один фазе наз волновой повер-ю. Крат расст между сосед волновыми поверх наз длиной волны. =T -скорость олны T-период колеб Пусть волна движ ы доль х: (РИС) =х/ =0cos(t-/*x) /=k –волновое число =0cos(t-kx) ур волны При волновых процессах перем-ся энер-я. 0cost =0cos(t-) |
|




 усть
ток течет по тонкому прямому
проводнику,найдем инд-ю магн.поля:dB=
μ0IdLsinα/4πr^2;
r*sinα=r0;
dL0=dLsinα;
dL0=rdL;
dB=
μ0I(sinα)^2r0dL/4πr0^2sinα=
μ0IsinαdL/4πr0;
B=∫dB=μ0I/4πr0∫{α1;
α2}
sinαdα;
B=μ0I(cosα1-cosα2)/4πr0-индукция
магнитн.поля тока прямого проводника
конечной длины B=μ0I/2πr0-индукция
магнитн. поля тока бесконечно длинного
прямого проводника
усть
ток течет по тонкому прямому
проводнику,найдем инд-ю магн.поля:dB=
μ0IdLsinα/4πr^2;
r*sinα=r0;
dL0=dLsinα;
dL0=rdL;
dB=
μ0I(sinα)^2r0dL/4πr0^2sinα=
μ0IsinαdL/4πr0;
B=∫dB=μ0I/4πr0∫{α1;
α2}
sinαdα;
B=μ0I(cosα1-cosα2)/4πr0-индукция
магнитн.поля тока прямого проводника
конечной длины B=μ0I/2πr0-индукция
магнитн. поля тока бесконечно длинного
прямого проводника B=
μ0IdLsinα/4πr^2=|α=π/2|=μ0IdL/4πr^2;
B=∫dB;
∫{L}dB2=0;
B=∫{L}dB1;
dB1=dBsinβ=dBR/r=dBR/
√R^2+r0^2;
dB1=μ0IRdL/4π(R^2+r0^2)√R^2+r0^2;
B=
μ0IR/4π(R^2+r0^2)^(3/2)∫{0;2πR}dL=
μ0IR^2/
2(R^2+r0^2)^(3/2);-индукция
магнитн.поля на оси круговго
витка.Частн.случай:М совпадает с 0:B=
μ0IR^2/2(R^2)^(3/2)=
μ0I/2R.Линии
инд.поля:
B=
μ0IdLsinα/4πr^2=|α=π/2|=μ0IdL/4πr^2;
B=∫dB;
∫{L}dB2=0;
B=∫{L}dB1;
dB1=dBsinβ=dBR/r=dBR/
√R^2+r0^2;
dB1=μ0IRdL/4π(R^2+r0^2)√R^2+r0^2;
B=
μ0IR/4π(R^2+r0^2)^(3/2)∫{0;2πR}dL=
μ0IR^2/
2(R^2+r0^2)^(3/2);-индукция
магнитн.поля на оси круговго
витка.Частн.случай:М совпадает с 0:B=
μ0IR^2/2(R^2)^(3/2)=
μ0I/2R.Линии
инд.поля:
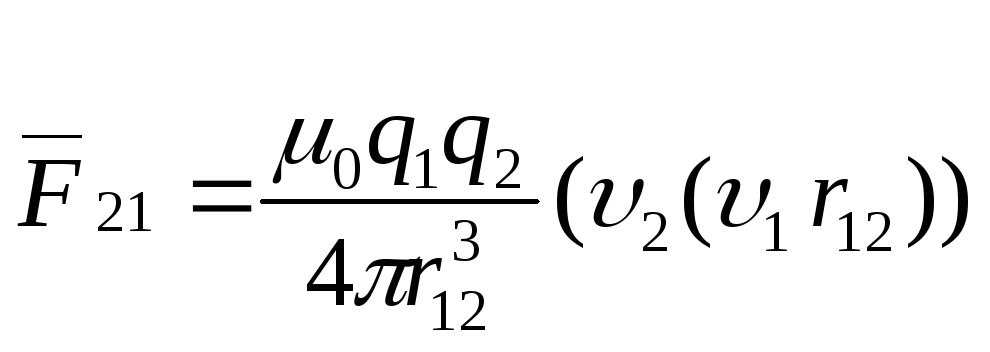 - сила, действующая на q2
со стороны q1
- сила, действующая на q2
со стороны q1
 -индукция
м.п. движущегося заряда
-индукция
м.п. движущегося заряда - сила, действующая на q2
со стороны q1
- сила, действующая на q2
со стороны q1
 -индукция
м.п. движущегося заряда
-индукция
м.п. движущегося заряда деальная
система сост из матер (.), подвешенной
на нити находящийся в поле силы тяжести.
F=mgsinα
x=-lα,
при малом угле α его синус = самому
углу, тогда F=-mgx/l
Сила не явл по своей природе упругой,
но так же зависит от смещения как и
упругая сила (Fy=-kx),
наз квазиупругой силой. Эта сила
приводит к гармоническим колебаниям
W20=g/l
T=2π√(l/g)
– период мат маятника. На практике
используют физический маятник – это
твердое тело, любой формы, закрепленное
на оси, не проходящей ч/з его центр
масс. Сила тяжести создает момент
вращения, величина которого зависит
от угла отклонения и будет меняться
со временем. Период гарм кол зависит
от момента инерции тела и ускорения
свободного падения. T=2π√(l/g)
деальная
система сост из матер (.), подвешенной
на нити находящийся в поле силы тяжести.
F=mgsinα
x=-lα,
при малом угле α его синус = самому
углу, тогда F=-mgx/l
Сила не явл по своей природе упругой,
но так же зависит от смещения как и
упругая сила (Fy=-kx),
наз квазиупругой силой. Эта сила
приводит к гармоническим колебаниям
W20=g/l
T=2π√(l/g)
– период мат маятника. На практике
используют физический маятник – это
твердое тело, любой формы, закрепленное
на оси, не проходящей ч/з его центр
масс. Сила тяжести создает момент
вращения, величина которого зависит
от угла отклонения и будет меняться
со временем. Период гарм кол зависит
от момента инерции тела и ускорения
свободного падения. T=2π√(l/g)



 (1)
(1)