
Шпоры по вычмату
.doc|
1.Метод простой итерации. Решим
систему Ах=В (1), А= |
2.Метод Зейделя. Основная идея: при вычислении (К+1)-го приближения неизвестной Хi учитываются уже вычисленные ранее (К+1)-е приближение х1,х2,… Пусть дана приведенная лин. система Хi=βi+(∑ от j=1 до n)£ij*xiK Предпол. что К-е приближ. известны тогда (К+1) имеет вид Xn(K+1)=βn+(∑ отj=1 до n-1) £niXj(K+1) + £nnXn(K). Достаточное условие: 1) ∑(от i=1 до n)|Aij|<1 для любого y 2) ∑(от j=1 до n)|Aij|<1 для любого i Следствие: для сист. метод итер. сходит. если все модули диагонал. коэффициентов для каждого Ур-ия >, суммы модулей всех остал. коэффиц. |Aii| <(i≠j)|Aij|. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3.Достаточные условия сходимости процесса итерации (доказать) Теорема: процесс итерации для системы Х=£x+β сх. к единств. решению если какая либо норма матр. £<1 или ||£||<1, xK=£x(K-1)+β, Док-во: постр. последов. приближен., таких, что XK=(£(K-1) +£(K-2)+…+ £+E)β+£KX0 Т.к. норма матр.<1, то норма £к→0, при к→∞ E+£+£2+…+£K-1=(∑от n=0 до K-1) £n| ||£||<1 |=(E-£)-1 X=lim(k→∞)Xк=lim[ (£(K-1) +£(K-2)+…+ £+E)β+£KX0 ]=(E-£ )-1β Сходимость доказана. |
4. Отделение корней уравнения. Отделение корней может происходить аналитически или графически. F(x)=0 X*- решение( F(X*) =0). Т. Если непрерывная ф-ция F(x) принимает значения различных знаков на [a,b], т.е F(a)*F(b)<0,то внутри этого отрезка содержится по крайней мере один корень уравнения F(x)=0
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5. Метод половинного деления. Будем решать ур-ние f(x)=0 на [a,b], известно, что f(a)*f(b)<0. Найти X такое [x-x*] < ε. Метод состоит в последовательном построении интервалов [an, bn], вложенных друг в друга и содерж. реш. X*. Пусть a0=a, b0=b предпол. что [ai,bi]промежуток построения, причем f(ai)*f(bi)<0 т.е. X* Є[ai,bi] найдем (.)Ci=(ai+bi)/2. Если f(ci)=0 то (ci) точное решение, если f(ci) ≠ 0 то: либо 1) f(ai)*f(сi) < 0, тогда a(i+1)=ai*b(i+1)=ci, либо 2) f(ci)*f(bi)<0, тогда то a(i+1)=ci, b(i+1)=bi В любом случае получ. интервал вдвое меньше исходного, причем f(ai+1)*f(bi+1) < 0 Процесс заканчив. либо 1)|ai-bi|<E,тогда (F(ci)=0),ci- –выбир. любую (.) и приним. ее за решен. ОЦЕНКА точности. f(ai)*f(bi)<0; bn-an=1/2n X(с чертой)-an<=1/2n (b-a) k-кол-во шагов k=log2((b-a)/E)+1. Решение нелин. ур-ий . Решен. осущ. в 2 этапа 1) локализация корней , т.е. нахожд. промежутков [a,b] котор. принадл. корень ур-ия 2)уточнение корней ,т.е. решение с задан. точностью. |
6. Метод хорд. Пусть
дана ф-ция F(x) = 0 на [a, b], причем F(a)*F(b) <
0. Для определенности предпол., что
F(a)<0 а F(b)>0, тогда поделим отрезок
[a,b] на F(a)/F(b). (x-a)/(b-a)=(y-f(a))/(f(b)-f(a));
Допустим X=X1,
y=0;
X1=a
– (f(a)
/ (f(b)-f(a)))*(b-a)
по этой ф-ле можно записать итерац.
процесс X1=a+h,
где
h1=-f(a)/(f(b)-f(a))
Докаж. сходим. итер. процесса будем
предполагать, что корень f(x)
определен и
1 2)
a<0
Т.е.1) неподвиж. тот конец , для кот. знак ф-ции совпад. со знаком втор. производ. 2)Послед. приближен. Xn лежат по ту сторон. X*, где f(x) имеет знак противоп знаку ее 2-ой произв. Критерий остановки |Xn+1 - Xn|< ε
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
18,19. Метод скорейшего спуска решения линейных систем Есть
система
Предположим,
что все fi
непр. дифф., рассм. Ф-цию U(x)
= (
U( Пусть
выразим отсюда p и подставим значение U = 2WTf(x). В итоге получим: xp+1=xp-pWT(xp)f(xp), где p = 2p = (fp,WpWpTfp)/( WpWpTfp, WpWpTfp) Для
линейных систем вида |
18. Метод скорейшего спуска решения систем.(grad) G Очевидно
что u(x(0))>(u(x(1)))>(u(x(n))), т.е. прийдём к
(.) мин ф-ии, а этот минимум явл реш исх
сист (рис1),
grad U.
X(p+1)=x(p)
- Лp
(Примечание (Л – лямбда)) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
21. Нахождение остаточного члена формулы трапеций. Рассмотрим остаточный член для 1-го звена, а остальные просуммируем Предположим, что ф-ция f дважды дифференцируема. Получим ф-цию
R(h)
=
- (h/2)*y’(x0+h) = (1/2)*(y(x0+h) - y(x0)) - (h/2)*y’(x0+h) R”(h) = (1/2)*y’(x0 + h) - (1/2)*y’(x0 + h) - (h/2)*y”(x0 + h) = - (h/2)*y”(x0 + h) R(0)=R’(0)=R”(0)=0. Проинтегрируем по h и воспользуемся теоремой о среднем
Теперь просуммируем остаточные члены для одного звена и получим полный R(h) = - (h3/12)*y”(ci), ci(xi-1, xi) Далее, (.) c[a, b], такая что (y”(ci))/n = y”(c) => R(h) = - (h3/12)*n*y”(c) => R(h) = - (b-a)*h2*y”(c)/12, c[a, b] На практике: Ih = h + Mh2, I2h = 2h + 4Mh2 => R = (h - 2h)/3
|
22.Формула СИМПСОНА (парабола).
∫f(x)dx
(рис.). Число разбиен. должно делиться на 4, чтобы можно было вычислить суммы с шагом 2h. Пары интервалов, следующие друг за другом, начиная с первой, будем “накрывать” параболой, проход. через 3 (.)-ки y=A0+A1x+A2x2; (x0,y0), (x1,y1), (x2,y2). Предпол что x0 = 0 => x1 = h, x2 = 2h. Для нахожд. A0,A1,A2 подстав. эти (.)-ки в ур-ие параб. => y0 = A0; y1 = A0+A1h+A2h2; y2=A0+2A1h+4A2h2; Получим, A0 = y0; A1 = (-3y0 + 4y1 - y2)/2h; A2 = (y0 - 2y1 + y2)/2h2 Площадь
одного эл-та (зависит от h
и значений ф-ции в выбранных точках)
=
Подставл знач-я А0, А1, А2 получ. In=(h/3)*(yn-2 + 4yn-1 + yn); In
=
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
23. Оценка погрешности в методе Симпсона. Предположим, что ф-я y непрерывна и трижды дифференцируема. Запишем ошибку для первого интервала в виде:
Продифференцируем эту ф-ю 3 раза. R’(h) = y(x1+h) – y(x1-h) – (1/3)[y(x1-h) + y(x1+h) + 4y(x1)] – (h/3)*[-y’(x1 – h) + +y’(x1+h)] R”(h) = - (1/3)y’(x1-h) + (1/3)y’(x1+h) – (h/3)[y”(x1-h) + y”(x1+h)] R”’(h) = -(h/3)[y”’(x1-h) - y”’(x1+h)] = -(2h2/3)*yIV(c4), c4(x1-h, x1+h) Теперь будем интегрировать:
R”(h)
=
R’(h) =
R(h)
=
На практике: Rh = Mh4, R2h = 16Mh4; R = (h - 2h)/15 |
10. Комбинированный метод. f(x)=0 : (a,b) : f(a)*f(b)<0 имеем 4 случая:
Расм. только 1-ой случай т.к. оставшиеся случаи либо сводяться к нему либо аналогичны. _
X*
Є (a,b)
x0=a
x0=b
Если допустимая
погрешность задана u=E,
то как только
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
20.Формула ТРАПЕЦИИ. Разобьем отрезок [a; b]
н [x0,x1], [x0,x2], …, [x0,xn] шаг h = (b-a)/n yi=f(xi) Ф-ла ТРАПЕЦИИ:
|
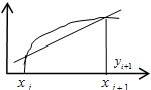
24. Метод Эйлера решения дифференциальных уравнений
y’=f(x,y); y(x0) = y0 - задача Коши. Разобьем ось х на промежут. xi = x0+i*h (рис.) В (.)M0-пров. касател. до пересеч. с прямой х = х1, получим (.)M1. y1 = х1 M1 Через (.) (x1, f(x1, y1)) пров касат до пересечения с прямой x = x2, получим M2 и тд Получ. Ломаную M0M1M2… считаем решением. Аналитически: f(xi,yi) = y’ (yi+1 - yi)/h => yi+1 = yi + h*f(xi,yi)-ф-ла облад. малой точностью.(порядка h2); y(xi+h)=y(xi)+y’(xi)h остал. члены разлож. в ряд Тэйлора (y(x)=y(x0)+y’(x0)(x-x0)+y”(x0)(x-x0)2/2!-поэт. точность порядка h2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
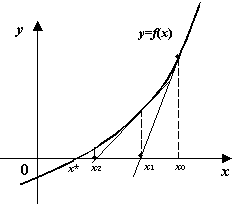
7. Геометрическая иллюстрация метода касательных.
Г |
8. Теорема о методе касательных. Если ф-ия f(a)*f(b)>0, причем вторая призводная сохраняет знак на отрезке [a,b], то исходя из любого начального приближения х0Є[a,b], удовл. условию f(х0) f”( х0)>0 то можно вычислить корень ур-я с любой степенью точности. Док-во: f(a)<0; f(b)>0; f”(x)>0; f’(x)>0, т.е. f(b) f”(b)>0 x0=b. Методом индукции докажем что, все xn>x*. Т.е. f(xn)>0, очевидно х0>x*. Путь хn>х*. Представим х*=хn+(х*-хn) по форм. Тейлора f(x*)=f(xn)+f’(xn) (х*-хn)+1/2 f”(xn) (х*-хn)2, тогда f(xn)-f’(xn) (х*-хn)<0 хn+1=xn(+)-f(xn)/f’(xn)>x*. Ч.т.д. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9. Видоизмененный метод касательных.
X Геометрически прямая параллельная первой касательной . т.е. здесь касательная заменяется на прямую, паралл. первой касательной |
12. Теорема о сходимости метода итераций.
Пусть φ(х)
опред. и диф. на [a,b]
тогда, если сущ. дробь q
такая
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11. Метод итерации.
f(x)=0,
заменим это ур-е равносильным x=f(x)
и построим приближение x2=f(х1),…xn+1=f(x).
Если эта последовательность существует
и сходиться, т.е. сущ. Предел
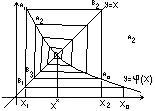
Если φ(х) возр. то получается лестницей, если убыв. то строится по спирали. |
16. Метод Ньютона решения систем. или _F(_x)=0. Предположим что найдено _х=(х1(p), х2(p),… хn(p)) одного из его корней, тогда точный корень _х=_х(р)+_Е(р)
_
F’(x)=w(x)=
Иначе F’(x)=w(x)=[fi / xj] i, j=_(1,n) и исходная система примет вид (x(p))+w(x(p))E(p)=0 Подставив в исходное мы получим x(p+1)=x(p)-w-1(_x(p))_F(_x(p)) сист методом Нютона. (Примечание: _X – иск с чертой) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
17. Теорема о сход-ти метода Ньютона. Модиф-ный метод Ньютона. Теорема Пусть дана _f(_x)=0, где
(_f(_x)=
Якобиант w(x(0))=[ fi(x(0)) / xi(x(0))] имеет обратную матрицу w -1(x(0))=Г0 причем ||Г0||=<А0, ||Г0f(x(0))|| =<B0, | 2fi(x)/ xixj | =< C. Получим пост удовлет условию μ0=2nА0В0С<1 Тогда процесс Ньютона X(p+1)=x(p)-w -1(x(p))f(x(p)) – сх. Причём x=lim(n∞)x(p) |x - x(p) |=<2B0 Под нормой матрицы понимается ||A||=max(i) |aij|. Метод простой итер. X(p+1) – w -1(x(0))f(x(0)) явл модифиц методом Ньютона и соотв теорема о сходимости метода прост итер аналогична теореме сх метода Ньютона
|
15. Метод простой итераций решения систем общего вида.
_х(р+1)=_φ(_х(р)) - ур-е в итер процессе Если итерационный проц сх, то он сх к корню векторного ур-я. Т.к. проц итер для ур-ий Xр+1= φ(х(р)) сх только в случае | φ’(x)|<1, то такое же усл мы получим и для сист аналогично найдём множитель, который даст возможность удовлет усл | φ’(x)|<1 Рассмотрим в общем виде сист ур-й _F(_x)=0. представим её в виде: _х=_х+Л_F(_х); в данном случае Л неособенная матрица, т.е опр ≠ 0. _х=_φ(х), где φ(_x)=_х+Л_F(_х) Для послед ур-я применим метод итер. φ(_x)=Е+Л_F’(_х) т.к. норма этой матрицы должна быть мала, выбираем Л из усл-я _φ’(_х(0))=Е+ЛF’(_x(0))=0 Л = - [F’(_x(0))]-1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
13. Выбор коэффициента в методе итераций. Нужно учитывать что в у-ии х= φ(х), φ(х) должно удовлет усл φ(х)<1. Этого можно добиться таким способом Рассмотр ур-е F(x)=0 это ур-е равносильно х=х-ЛF(x)=> φ(х)=ч-ЛF(x), где парам Л выбирают таким образом что бы 0=<1-ЛF’(x)=<q<1 По условию задачи m1=<F’(x)=<M1(наиб и наим значение) на [a;b] => Л=1/M1 (Примечание (Л – лямбда)) |
14.
Метод
итераций решения нелинейных систем
второго порядка
При локализации корня графич. способом, удобно эти значения применять за нулевое приблежение. Из 1-ого ур-я явно выразим х, а из 2-ого у.
Lim(n
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
31.Формула Ньютона для разностных узлов. ∆y0 = y1-y0 ∆y1= y2-y1 ∆y2= y3-y2 ∆yn-1 = yn - yn-1 ∆y0 = y1-y0 ∆2y0 = ∆y1- ∆y0 = y2 – y1 – y1 + y0 = y2 – 2y1 + y0 ∆3y0= ∆2y1- ∆2y0 = y3 – 3y2 +3y1 – y0 ∆ky0 = yk – kyk-1 + ((k(k-1))/2!)yk-2 + ((k(k-1)(k-2))/3!)yk-3 + ...+ (-1)Ky1 Запишем эту формулу для значения разности в узле xi: ∆kyi = yk+i – yk+i-1 + ((k(k-1))/2!)yk+i-2 yk=y0 +k∆y0 +((k(k-1)/2!)∆2y0 + … ∆ky0 Построим интерполяционный многочлен Ньютона: N(x)= a0 +a1(x-x0) +a2(x-x0)(x-x1) +a3(x-x0)(x-x1)(x-x2) + … an(x-x0)(x-x1)…(x-xn-1) Этот многочлен должен проходить через заданные узлы, поэтому: N(x0)= a0=y0 N(x1)= a0 +a1(x-x0) = a0 + a1h=y1 N(x2)= a0 +2a1h+ 2a2h2 = y2 Отсюда найдём коэффициенты: a0=y0 a1= (y1-y0)/h=∆y1/h a2=∆2y0/2h2 Следовательно, любой коэффициент имеет вид: ak = ∆ky0/k!hK и полином Ньютона будет иметь вид: N(x)=y0+ (∆y0(x-x0))/h + (∆2y0(x-x0)(x-x1))/2!h2 + … + (∆ny0(x-x0)(x-x1)…(x – xn-1))/n!hn Запишем его иначе: пусть (x-x0)/h =q тогда N(x) =(y0 +q∆y0∆2y0q(q-1))/2! + … + ∆ny0(1/n!)q(q-1)(q-2)…(q-n+1) Многочленами Ньютона пользуются в случае равноотстоящих узлов.
|
32.Приближенное дифференцирование. Постановка краевых задач
Пусть имеем
функцию y(x)
заданную в равноотстоящих точках.
Запишем многочлен Ньютона для этой
функции y(x)=
y0+q∆y0+(q(q-1)
∆2y0)/2
+ (q(q-1)(q-2)∆3y0)/3!
+ (q(q-1)(q-2)(q-3)∆4y0)/4!
Для нахождения производной функции
будем искать производную этого
многочлена h=xi+1-xi;
q=(x-x0)/h
y(x)=
y0+q∆y0+
((q2-q)∆2y0)/2+((q3-3q2+2q)∆3y0)/3!
+ ((q4-6q3+4q2-6)
∆4y0)/4!+…
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
33.Метод конечных разностей y’i= (yi+1-yi)/h y’’i = (y’i+1-y’i)/h = ((yi+2-yi+1)/h-(yi+1-yi)/h)/h=(yi+2-2yi+1+yi)/h2 т.е для нахождения производной 1 порядка нужно знать значения ф-ции в 2 узлах. Для нахождения производной второго порядка нужно знать значения ф-ции в 3 узлах. Пользуются следующей разностной схемой:1)разбивают отрезок [a,b] точками a=x0,x1, x2,…,xn=b 2)y’i=(yi+1-yi-1)/2h 3) y’’i=(yi+1-2yi+yi-1)/h2 4)y’0=(y1-y0)/h 5) y’n = (yn-1 – yn)/-h Будем рассматривать д.у 2 порядка: y” +p(x)y’+q(x)y =f(x) при заданных условиях α0y(a)+ α1y’(a)=A β0y(b)+ β1y’(b)=B │α0│+│α1│≠0 │ β0│+│ β1│≠0 Исходная система может быть представлена в виде разностной схемы (yi+1–2yi+yi-1)/h2+pi(yi+1-yi-1)/2h +qiyi=fi, где pi, qi, fi –значения коэффициентов в точках xi. α0y0+ (α1(y1-y0))/h=A β0yn+ (β1(yn-1-yn))/-h=B Решив эту систему получим таблицу значений искомой функции y |
35.Уравнение Лапласа в конечных разностях
Б |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
34 .Метод прогонки Будем рассматривать д.у 2 порядка: y” +p(x)y’+q(x)y =f(x) при заданных условиях α0y(a)+ α1y’(a)=A β0y(b)+ β1y’(b)=B │α0│+│α1│≠0 │ β0│+│ β1│≠0 Исходная система может быть представлена в виде разностной схемы (yi+1–2yi+yi-1)/h2+pi(yi+1-yi-1)/2h +qiyi=fi (1), где pi, qi, fi –значения коэффициентов в точках xi. α0y0+ (α1(y1-y0))/h=A β0yn+ (β1(yn-1-yn))/-h=B Будем использовать метод прогонки Из ур (1) можно получить yi+1+miyi+niyi-1=f^ih2 (4) где коэффициенты имеют вид: mi=(2-qih2)/(1+pih/2) ni= (1-pih/2)/(1+pih/2) f^i=fi/(1+pih/2) Из уравнения (4) выразим yi yi=f^ih2/mi – (1/mi)(yi+1)-(ni/mi)(yi-1) (5) Предположим, что с помощью системы (2), (3), (4) из ур-ния (5) исключено yi-1,тогда yi= ci(di-yi+1) (6) Из ур (6) можно записать yi-1= ci-1(di-1-yi) Подставляя это уравнение в ур-ние (4) получим yi+1+miyi+nici-1di-1-yi=f^ih2 Отсюда выразим yi yi=( f^ih2- nici-1di-1-yi+1)/(mi-nici-1) Исходя из сравнения полученных формул получим ci=1/mi-nici-1 di=f^ih2-nici-1di-1 c0= α1/ (α0h - α1) d0=Ah/ α1 На основании этих формул последовательно определяются сi и di при i=1 до n-1 включительно Обратный ход начинается с вычисления yn Вычислив yn по ф-ле (6) определяются все остальные значения y |
36.Метод сеток. Построение шаблонов Пусть в плоскости XOY имеется область G с границей Г, построим на плоскости два семейства параллельных прямых x= x0+ih y=y0+kh
В
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
25. Модифицированный метод Эйлера. В отличии от метода Эйлера, когда для вычисления следующей точки (Xi+1, Yi+1) требуется информация только Y предыдущей точки. Мод. метод предполагает знание о нек-ой промежуточной точки xi+1/2=xi+h/2 и xi+1/2=xi+(h/2)*fi. Метод заключается: 1) через точку (xi,yi) проводится кас-ая с tg наклона tgα=f(xi,yi) до х с прямой x=xi+1/2. В полученной точке х по методу Эйлера выч-ся знач-я ф-ии y=yi+1/2 и выч-ся знач-е производной fi+1/2=f(xi+1/2, y=yi+1/2). Знач-е этой производной определяет tg угла наклона 2-ой производной, кот. проводится из полученной точки. 2) Затем возвр-ся в исходную точку и через неё проводим прямую, парал 2-й кас-ой. |
26. Усовершенствованный метод Эйлера.
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
28. Интерполирование функций. Постановка задачи.
П
|
27. Метод Рунге-Кутта.
Обычно говорят,
что метод Р-К явл. Методом 4 и 5 порядка
точности, т.е. (h4,h5).
Точно вычислить погрешность этого
метода затруднительно, т.к. исходя из
текущего значения y(xi)
вычисляют величину y(xi+2h)
2-мя способами. 1 раз с шагом h,
другой с шагом 2h.
Если расхождение полученных значений
не превышает допустимой погрешности,
то шаг выбран правильно и полученное
значение можно принять за верное, в
противном случае шаг уменьшают в 2
раза. Мы решаем ур-е
Выбирается шаг
h,
наносится сетка xi+1=x0+hi.
Рассматривают
числа
k1(i)=h*f(xi,yi);
k2(i)=h*f(xi
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
30. Формула Лагранжа.
Будем считать
данную ф-ию f(x)
и полином Qm(x)=a0+a1x+a2x2…+amxm
близкими, если они совпадают на заданной
системе точек x0,x1,x2…xn.
Задача состоит в том, чтобы построить
многочлен возможно низшей степени m,
принимающий в данных точках известные
значения. По основной теореме алгебры
можно предположить, что m=n.
Исходя из условия задачи, можно записать
систему линейных уравнений. |
29. Конечные разности.
П
Т.е. все разности чётного порядка располагаются в тех же гор. Строках, что и аргументы. А нечётные – в промежуточных строчках.
|

 х=
х=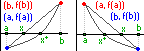 )a>0
)a>0
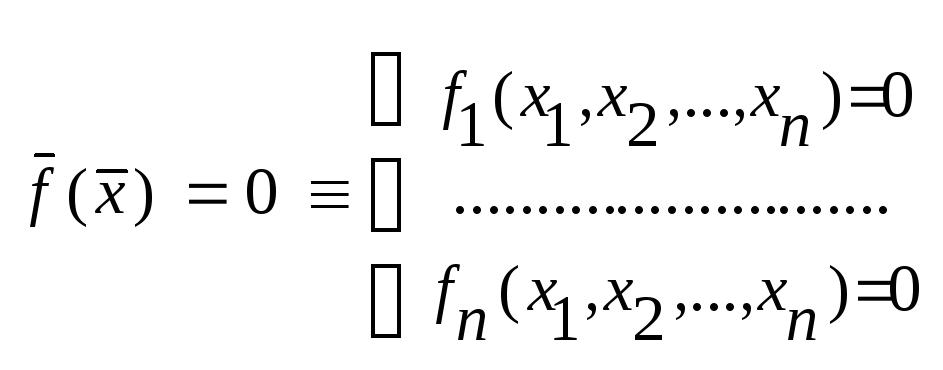
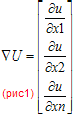 rad-задаёт
направление. Предположим что все fi
непрерыв диф-мы Рассмотрим ф-ю
u(x)=(_f(_x);_f(_x))= ф-я сама на себя скалярная
=
(i
от 1 до n)(fi(_x))2.
Очевидно что каждое решение исход
сист обращ в 0 ф-ю u(x) и наоборот те числа
обращают в 0 ф-ю u(x) явл решеним исх
сист. Предположим что исх сист имеет
лишь решения которые явл (.) мин ф-ии u
таким образом задача сводится к
нахождения (.) мин ф-ии u. Пусть _х –
решение сист _х(0) – нулевое приблежение.
В (.) _х(0) проведём поверхность уровня
u(x)=u(xi0), если нач (.) близка к решению,
то поверхность похожа на эллипсоид .
Из(.) х(0) будем двигаться по нормали
поверхности u(x)=u(x0) до тех пор пока
нормаль не каснётся другой поверхности
уровня u(x)=u(x(1)) Затем отправляемся из
(.) х(1) по нормали поверхности уровня
u=u(x(1)) до тех пор пока эта нормаль не
каснётся поверхности уровня в (.) х(2)
и т.д.
rad-задаёт
направление. Предположим что все fi
непрерыв диф-мы Рассмотрим ф-ю
u(x)=(_f(_x);_f(_x))= ф-я сама на себя скалярная
=
(i
от 1 до n)(fi(_x))2.
Очевидно что каждое решение исход
сист обращ в 0 ф-ю u(x) и наоборот те числа
обращают в 0 ф-ю u(x) явл решеним исх
сист. Предположим что исх сист имеет
лишь решения которые явл (.) мин ф-ии u
таким образом задача сводится к
нахождения (.) мин ф-ии u. Пусть _х –
решение сист _х(0) – нулевое приблежение.
В (.) _х(0) проведём поверхность уровня
u(x)=u(xi0), если нач (.) близка к решению,
то поверхность похожа на эллипсоид .
Из(.) х(0) будем двигаться по нормали
поверхности u(x)=u(x0) до тех пор пока
нормаль не каснётся другой поверхности
уровня u(x)=u(x(1)) Затем отправляемся из
(.) х(1) по нормали поверхности уровня
u=u(x(1)) до тех пор пока эта нормаль не
каснётся поверхности уровня в (.) х(2)
и т.д.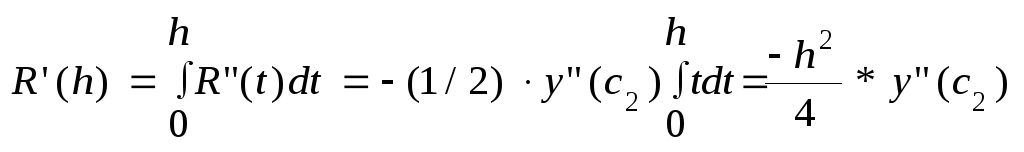 ,
c2(x0,
x0+h)
,
c2(x0,
x0+h)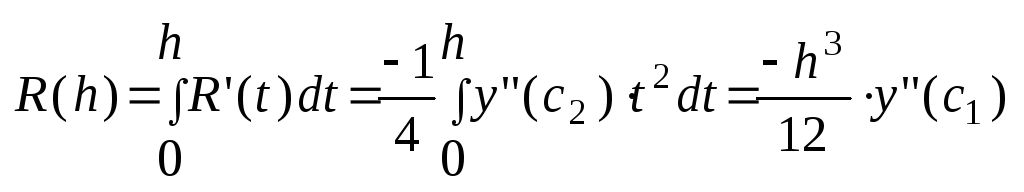 ,
c1(x0,
x0+h)
,
c1(x0,
x0+h)
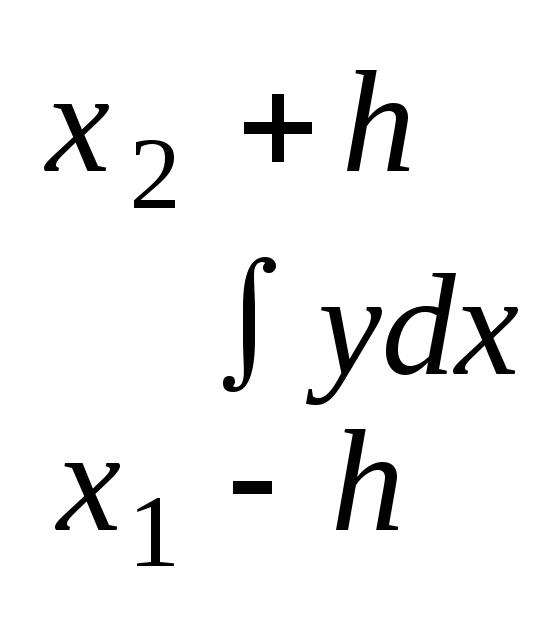 -
(h/3)*[y(x1-h)
+ 4y(x1)
+ y(x1+h)]
-
(h/3)*[y(x1-h)
+ 4y(x1)
+ y(x1+h)]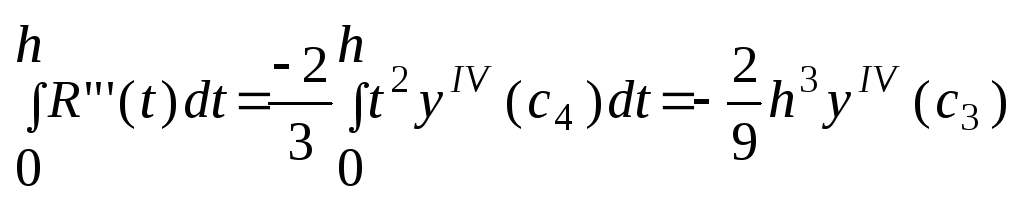 ,
c3(x1-h,
x1+h)
,
c3(x1-h,
x1+h)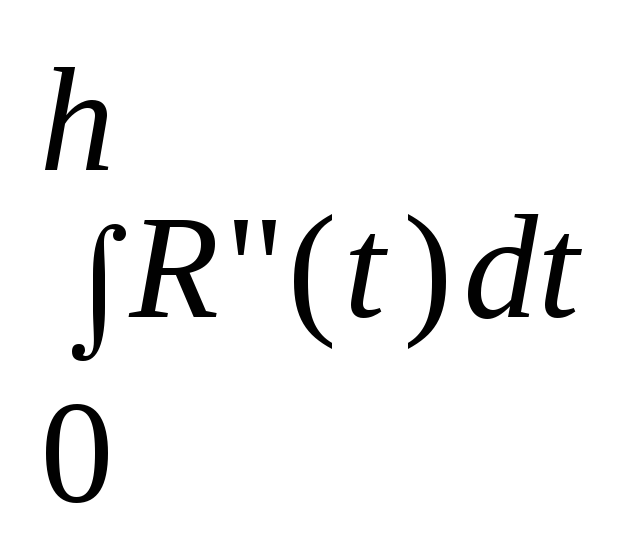 =
-(1/18)*h4*y4(c2),
c2(x1-h,
x1+h)
=
-(1/18)*h4*y4(c2),
c2(x1-h,
x1+h)
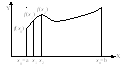 а
n
равных отрезков
а
n
равных отрезков
 еометрически
прямая параллельная первой касательной
. т.е. здесь касательная заменяется на
прямую, паралл. первой касательной.
еометрически
прямая параллельная первой касательной
. т.е. здесь касательная заменяется на
прямую, паралл. первой касательной.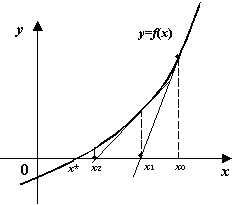 (n+1)=Xn-f(Xn)/
(n+1)=Xn-f(Xn)/
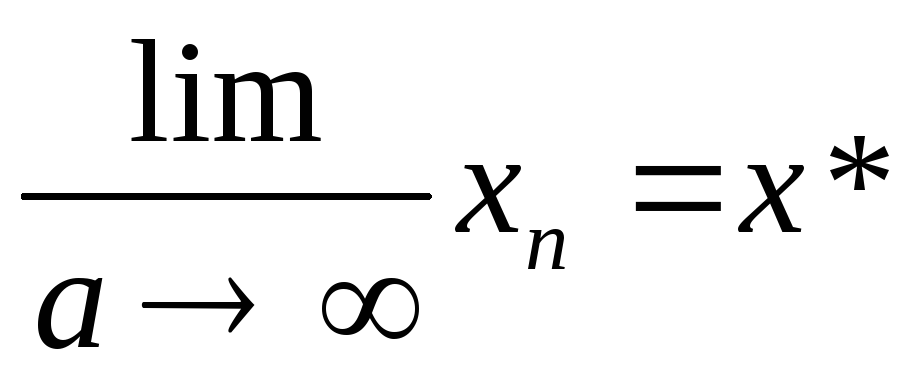 .Д-во:
рассмотр. xn=φ(x(n-1));
x(n+1)=φ(xn);
вычтем, по теорем. Лагранжа будем иметь
x(n+1)-xn=(xn-x(n-1))*
.Д-во:
рассмотр. xn=φ(x(n-1));
x(n+1)=φ(xn);
вычтем, по теорем. Лагранжа будем иметь
x(n+1)-xn=(xn-x(n-1))*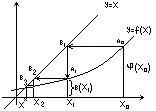
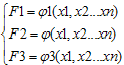 Е(р)=(Е1(р),
Е2(р), Е(р))-явл погрешностью (поправкой)
т.е. ур-е может быть записано
_F(_x(p)+_E(p))=0 Разложим левую часть ур-я
по степеням Е, ограничевшись линейными
членами _F(_x(p)+_E(p))=F’(_x(p))E(p)
Препишем это ур-е в развёрнутом виде
Fn(x1(1)+E1(p)…xn(p)+En(p))
= Fn(x1(p)…xn(p)) + F’nx1(x1(p)…xn(p))E1(p) +
Fn’x2(x1(p)…x(p))En(p) + F’nxn(x1(p)…x4(p))En(p)т.е.
матр F’(x)-явл
матрицей Якоби
Е(р)=(Е1(р),
Е2(р), Е(р))-явл погрешностью (поправкой)
т.е. ур-е может быть записано
_F(_x(p)+_E(p))=0 Разложим левую часть ур-я
по степеням Е, ограничевшись линейными
членами _F(_x(p)+_E(p))=F’(_x(p))E(p)
Препишем это ур-е в развёрнутом виде
Fn(x1(1)+E1(p)…xn(p)+En(p))
= Fn(x1(p)…xn(p)) + F’nx1(x1(p)…xn(p))E1(p) +
Fn’x2(x1(p)…x(p))En(p) + F’nxn(x1(p)…x4(p))En(p)т.е.
матр F’(x)-явл
матрицей Якоби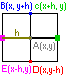
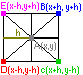 удем
решать δ2u/δx2+
δ2u/δy2=0
Будем
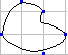
решать задачу Дирихле, т.е найдём
решение уравнения Лапласа в заданной
области, ограниченной контуром гамма
причём u(p)=φ(p)
PГ
для всех точек p
принадлежащих границе.Т.е на границе
области задана непрерывная функция.
Перейдём от дифура к его разностному
аналогу δ2u/δx2=
=(u(x+h,y)-2u(x,y)+u(x-h,y))/h2
δ2u/δy2=(u(x,y+h)-2u(x,y)+u(x,y-h))/h2
Подставим
u(x,y)=1/4(u(x+h,y)+u(x-h,y)+
u(x,y+h)
+u(x,y-h))
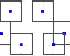
Это уравнение соответствует первой
разностной схеме. 1 осн схема изображена
на левом рисунке. 2 осн сх:
u(x,y)=1/4(u(x+h,y+h)+u(x+h,y-h)+
u(x-h,y-h)
+u(x-h,y+h))
И 1 и 2 схема являются точными до порядка
h2
удем
решать δ2u/δx2+
δ2u/δy2=0
Будем
решать задачу Дирихле, т.е найдём
решение уравнения Лапласа в заданной
области, ограниченной контуром гамма
причём u(p)=φ(p)
PГ
для всех точек p
принадлежащих границе.Т.е на границе
области задана непрерывная функция.
Перейдём от дифура к его разностному
аналогу δ2u/δx2=
=(u(x+h,y)-2u(x,y)+u(x-h,y))/h2
δ2u/δy2=(u(x,y+h)-2u(x,y)+u(x,y-h))/h2
Подставим
u(x,y)=1/4(u(x+h,y)+u(x-h,y)+
u(x,y+h)
+u(x,y-h))
Это уравнение соответствует первой
разностной схеме. 1 осн схема изображена
на левом рисунке. 2 осн сх:
u(x,y)=1/4(u(x+h,y+h)+u(x+h,y-h)+
u(x-h,y-h)
+u(x-h,y+h))
И 1 и 2 схема являются точными до порядка
h2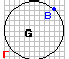 каждой внутренней точке заменим
исходное уравнение конечно-разностным
по 1 или 2 схеме. В граничных точках
u(Bh)=u(B)=φ(B),где
B-ближайшая
к границе точка. Для внутренних
узлов:ukij
=1/4(uk-1i-1,j+
uk-1i+1,j+
uk-1i,j-1+
uk-1i,j+1)
В граничных точках значения могут
быть поправлены по формулам линейной
интерполяции u0(Ah)=
u(a)=φ(A)
uk(Ah)=
u(a)+((
uk-1(B)-u(A))/(h+δ))δ
точка A
ближайшая к узловой точке Ah
границы Г B-ближайший
к Ah
внутренний узел сетки δ- удаление
узла Ah
от точки A.
Значение δ может быть как + так и –
Если узел расположен на границе uk(Ah)=
u(a)=φ(A)
При решении задачи для выбора u0ij
используют линейную интерполяцию.
Иногда для решения задачи используют
крупную сетку, а затем решают её же но
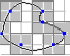
на более мелкой сетке. Построение
шаблонов. Для построения шаблонов
строим вторую сетку, линии которой
проходят посередине между линиями
первой, причём так, что узлы первой
сетки попадают в центры клеток 2 сетки
каждой внутренней точке заменим
исходное уравнение конечно-разностным
по 1 или 2 схеме. В граничных точках
u(Bh)=u(B)=φ(B),где
B-ближайшая
к границе точка. Для внутренних
узлов:ukij
=1/4(uk-1i-1,j+
uk-1i+1,j+
uk-1i,j-1+
uk-1i,j+1)
В граничных точках значения могут
быть поправлены по формулам линейной
интерполяции u0(Ah)=
u(a)=φ(A)
uk(Ah)=
u(a)+((
uk-1(B)-u(A))/(h+δ))δ
точка A
ближайшая к узловой точке Ah
границы Г B-ближайший
к Ah
внутренний узел сетки δ- удаление
узла Ah
от точки A.
Значение δ может быть как + так и –
Если узел расположен на границе uk(Ah)=
u(a)=φ(A)
При решении задачи для выбора u0ij
используют линейную интерполяцию.
Иногда для решения задачи используют
крупную сетку, а затем решают её же но
на более мелкой сетке. Построение
шаблонов. Для построения шаблонов
строим вторую сетку, линии которой
проходят посередине между линиями
первой, причём так, что узлы первой
сетки попадают в центры клеток 2 сетки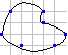




 )
через точку (xi,yi)
проводится касс-ая до х с прямой
xi+1/2=xi+h.
Угл. коэф-т этой кривой tgα1=f(xi,yi).
2) В полученной точке по методу Эйлера
выч-ся знач-е ф-ии yi+1=yi+h*(
f(xi,yi))
и выч-ся новая производная tg
α2=
f(xi,yi+1).
3) Далее происходит возврат в точку
(xi,yi)
и через нее проводится новая касательная,
где tg
угла наклона есть среднее арифметическое
2-ух предыдущих tg-енсов,
т.е. tgα
= (tgα1+
tgα2)/2
= (f(xi,yi)+F(xi+1,yi+1))/2.
Новое значение yi+1
= yi+h*((f(xi,yi)+F(xi+1,yi+1))/2).
)
через точку (xi,yi)
проводится касс-ая до х с прямой
xi+1/2=xi+h.
Угл. коэф-т этой кривой tgα1=f(xi,yi).
2) В полученной точке по методу Эйлера
выч-ся знач-е ф-ии yi+1=yi+h*(
f(xi,yi))
и выч-ся новая производная tg
α2=
f(xi,yi+1).
3) Далее происходит возврат в точку
(xi,yi)
и через нее проводится новая касательная,
где tg
угла наклона есть среднее арифметическое
2-ух предыдущих tg-енсов,
т.е. tgα
= (tgα1+
tgα2)/2
= (f(xi,yi)+F(xi+1,yi+1))/2.
Новое значение yi+1
= yi+h*((f(xi,yi)+F(xi+1,yi+1))/2).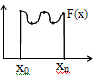 усть
на [a,b]
заданы (n+1)
точек x0,x1,…,xn
(эти точки наз-ся узлами интерполяции).
Известны значения нек-ой ф-ии в этих
точках: f(x0)=y0,
f(x1)=y1,
f(xn)=yn.
По этим точкам требуется построить
ф-ю F(x),
принадлежащую известному классу,
принимающую в узлах интерполяции
известные знач-я. В такой интерполяции
ф-ия F(x)
либо не однозначна, либо не сущ-ет
вовсе. Если же ф-ия F(x)=Pn(x)
имеет вид полинома степени не выше
степени n,
то такая задача имеет единственное
решение. Полученную интерполяционную
ф-ию F(x)
используют для нахождения значений
ф-ии в точках, отличных от узлов
интеропляции. Если эти точки принадлежат
промежутку [a,b],
то такая задача наз-ся интерполированием
в узком смысле. Если же точки выходят
за границы [a,b],
то такая задача наз-ся экстраполированием.
усть
на [a,b]
заданы (n+1)
точек x0,x1,…,xn
(эти точки наз-ся узлами интерполяции).
Известны значения нек-ой ф-ии в этих
точках: f(x0)=y0,
f(x1)=y1,
f(xn)=yn.
По этим точкам требуется построить
ф-ю F(x),
принадлежащую известному классу,
принимающую в узлах интерполяции
известные знач-я. В такой интерполяции
ф-ия F(x)
либо не однозначна, либо не сущ-ет
вовсе. Если же ф-ия F(x)=Pn(x)
имеет вид полинома степени не выше
степени n,
то такая задача имеет единственное
решение. Полученную интерполяционную
ф-ию F(x)
используют для нахождения значений
ф-ии в точках, отличных от узлов
интеропляции. Если эти точки принадлежат
промежутку [a,b],
то такая задача наз-ся интерполированием
в узком смысле. Если же точки выходят
за границы [a,b],
то такая задача наз-ся экстраполированием.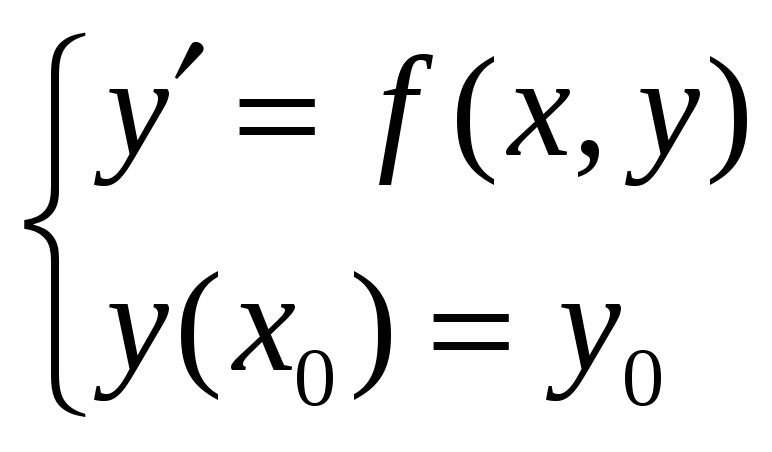
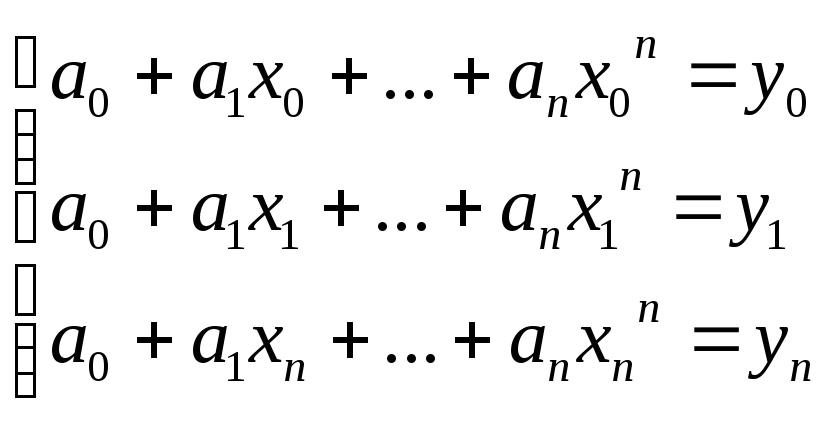 .
Эта система линейная, её можно решать
по формуле Крамера (определитель
Вандермода): Δ=
.
Эта система линейная, её можно решать
по формуле Крамера (определитель
Вандермода): Δ=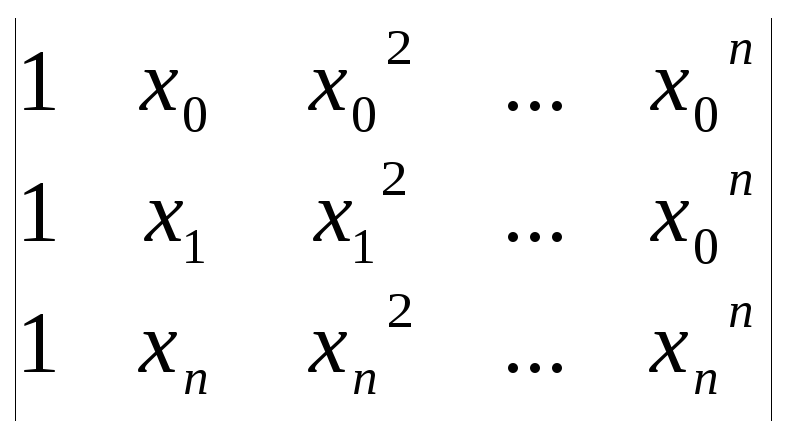 =П(xq-xp)
– произведение, где
=П(xq-xp)
– произведение, где
 усть
известны значения ф-ии y
= f(x)
в равноотстоящих узлах xk=x0+kh
(k=0,n):
y0=f(x0),
y1=f(x1),
yn=f(xn).
x
= x0(h)xn
– означает разбивку [x0,xn]с
шагом h.
Конечные разности I
(первого) порядка имеют вид: Δy0=y1-y0,
Δy1=y2-y1
и т.д. Конечные разности II
(второго) порядка: Δ2y0=
Δy1-Δy0,
Δ2y1=
Δy2-Δy1
и т.д. Конечные разности записываются
в виде таблицы:
усть
известны значения ф-ии y
= f(x)
в равноотстоящих узлах xk=x0+kh
(k=0,n):
y0=f(x0),
y1=f(x1),
yn=f(xn).
x
= x0(h)xn
– означает разбивку [x0,xn]с
шагом h.
Конечные разности I
(первого) порядка имеют вид: Δy0=y1-y0,
Δy1=y2-y1
и т.д. Конечные разности II
(второго) порядка: Δ2y0=
Δy1-Δy0,
Δ2y1=
Δy2-Δy1
и т.д. Конечные разности записываются
в виде таблицы: