2. Двойственные задачи линейного программирования

План.

2.1. Двойственный симплекс метод.

2.2. Экономическая интерпретация объективно обусловленных оценок и исследование задачи распределения ресурсов.

2.1. Двойственный симплекс-метод

Двойственный симплекс-метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами. В обычном симплексном алгоритме план всегда должен быть допустимым. Допустимый план — это такой план, который удовлетворяет всем ограничениям задачи при обязательном условии неотрицательности неизвестных, то есть любые числа в итоговом столбце положительны. План называется недопустимым (или условно-оптимальным), если в итоговом столбце имеются отрицательные числа, зато оценки целевой строки соответствуют целевой функции, то есть являются положительными при решении на максимум и отрицательными при решении на минимум. В процессе решения двойственным методом план является недопустимым. При использовании двойственного метода сначала применяют обычную симплекс-процедуру и добиваются того, чтобы все оценки соответствовали цели решения задачи, причем пока не обращают внимания на знаки чисел в итоговом столбце. Только когда такой условно-допустимый план достигнут, смотрят на эти знаки. Если в итоговом столбце оказались отрицательные числа, план изменяется так, чтобы недопустимость уменьшилась, а затем и исчезла, но чтобы двойственные оценки продолжали соответствовать при этом цели решения задачи. Возможность придавать в процессе решения отрицательные значения неизвестным, входящим в план, в случае, если ограничения заданы неравенствами, позволяет избавиться от искусственных неизвестных, это сокращает размеры задачи, а значит, и вычислений³.

Рассмотрим алгоритм решения задач двойственным симплексным методом.

1. Математическая модель прямой задачи линейного программирования должна быть в стандартной форме записи. В противном случае ее надо привести к стандартной форме записи.

2. Для прямой задачи составляется двойственная.

3. Обе задачи приводят к каноническому виду.

4. Выражают базисные переменные обеих задач через основные переменные.

5. Находят исходное решение прямой и двойственной задач и проверяют его на оптимальность. Для этого заполняют симплекс-таблицу двойственного симплекс-метода. Строки таблицы 1-го шага (верхние части клеток) заполняют по данным системы ограничений и целевой функции прямой задачи. Столбцы таблицы 1-го шага (верхние части клеток) заполняют по данным системы ограничений и целевой функции двойственной задачи.

Симплексная таблица двойственного симплекс-метода имеет следующий вид:

	yбаз	ym+1	ym+2		ym+n
yсв	xсв xбаз	- x1	- x2		- xn	bi
y1	xn+1	h11	h12		h1n	l1
y2	xn+2	h21	h22		h2n	l2
						
ym	xn+m	hm1	hm2		hmn	lm
cj		- c1	- c2		- cn

Решение является оптимальным, если в строке и столбце b_i нет отрицательных элементов.

В противном случае следует провести изменения в базисных переменных.

6. Выбор разрешающей строки. Находят отрицательный элемент в строке . В столбце над этим найденным элементом выбирают любой положительный элемент, эта строка – разрешающая.

Если в столбце над найденным элементом нет положительных элементов, то ПЗЛП не имеет смысла (целевая функция не ограничена в области допустимых решений), а ДЗЛП не имеет решения.

7. Выбор разрешающего столбца. Элементы строки делят на соответствующие элементы разрешающей строки под переменными. Из полученных отношений выбирают максимальное отрицательное отношение, этот столбец – разрешающий (максимальным из отрицательных отношений может быть отношение – отрицательный ноль).

Если среди полученных отношений нет отрицательных, то ПЗЛП не имеет решения, ДЗЛП не имеет смысла или решения.

На пересечении разрешающей строки и разрешающего столбца получен разрешающий элемент.

8. Заполнение нижних частей клеток таблицы. Под разрешающим элементом всегда ставят «1». Остальные элементы разрешающей строки переписываются без изменений. Остальные элементы разрешающего столбца переписываются с противоположным знаком. Остальные элементы таблицы находят по правилу прямоугольника: искомый элемент умножают на разрешающий и из этого произведения вычитают произведение элементов, расположенных на противоположной диагонали прямоугольника, образуемого искомым и разрешающим элементами (все элементы из верхних клеток).

9. Построение новой симплекс-таблицы. Изменяют базисные переменные: меняют местами переменные из разрешающей строки и разрешающего столбца. Элементы из нижних клеток предыдущей симплекс-таблицы делят на верхний разрешающий элемент и записывают на соответствующие места в верхние клетки новой симплекс-таблицы.

Если в новой таблице в строке есть отрицательные элементы, то следует сделать следующий шаг симплекс-метода. (Нецелесообразно выбирать за разрешающую строку – те же строки, что и на предыдущих шагах).

Если в новой таблице в строке нет отрицательных элементов, а в столбце свободных членов остались отрицательные элементы, то строка с отрицательным значением выбирается за разрешающую, и выполняется следующий шаг симплекс-метода.

Если в строке есть нулевой элемент, то это признак альтернативного оптимума для ПЗЛП. Для нахождения альтернативного решения выполняется еще один шаг симплекс-метода: Столбец с нулевым элементом в строке выбирается за разрешающий. Находят неотрицательные отношения столбца свободных членов к соответствующим элементам разрешающего столбца. Из полученных отношений выбирают минимальное неотрицательное отношение – это разрешающая строка, разрешающий элемент найден. Затем выполняют еще один шаг симплекс-метода.

Если в столбце есть нулевой элемент, то это признак альтернативного оптимума для ДЗЛП. Для нахождения альтернативного решения выполняется еще один шаг симплекс-метода. При этом строка с нулевым элементом в столбце выбирается за разрешающую.

Рассмотрим решение задачи двойственным симплекс-методом.

Канонический вид:

Выразим базисные переменные через свободные:

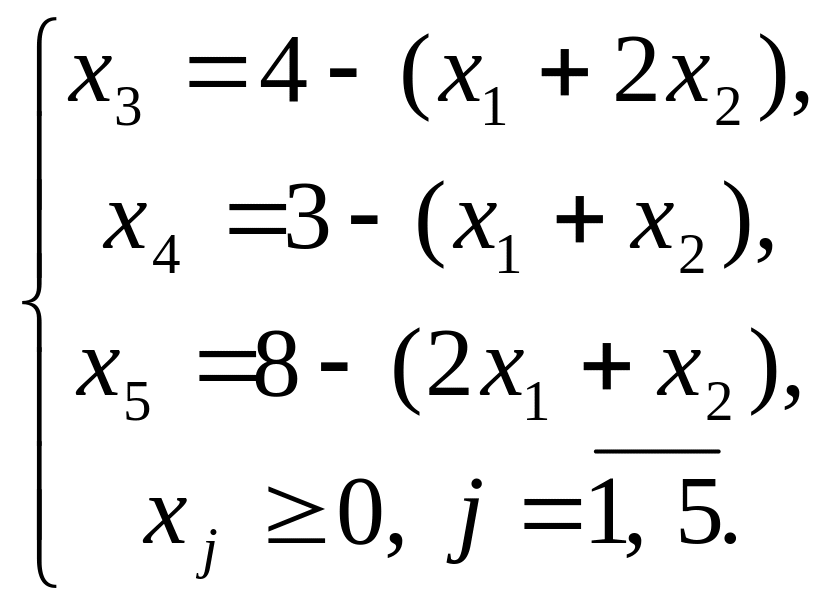
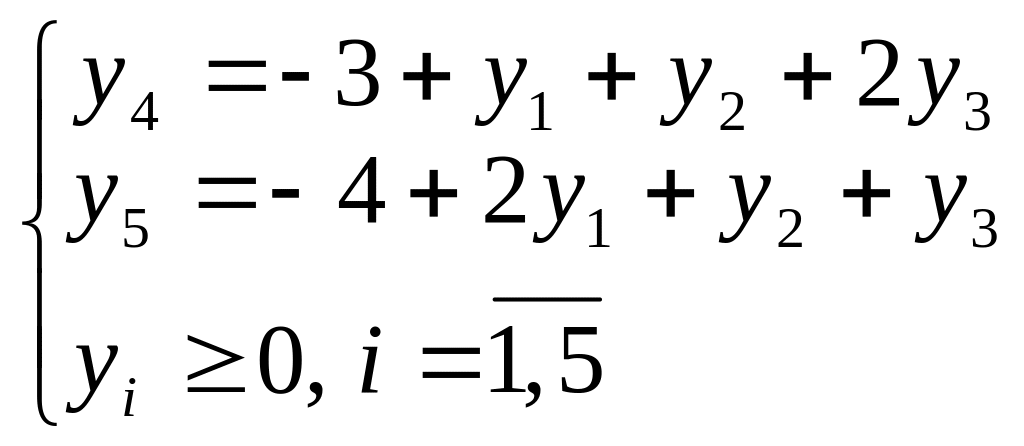
Введем соответствие основных переменных прямой задачи и дополнительных переменных двойственной задачи, а также дополнительных переменных прямой задачи и основных переменных двойственной задачи:

х1 y4

х2 y5

х3 y1

х4 y2

х5 y3

Составим симплекс-таблицу

	yбаз	y4	y5
yсв	xсв xбаз	- x1	- x2	bi
y1	x3	1	2	4
y2	x4	«1»	1	3
y3	x5	2	1	8
cj		- 3	- 4	0

Решение ПЗЛП выписывается по строкам, значения базисных переменных берутся из столбца b_i, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: = (0, 0, 4, 3, 8), = 0.

Решение ДЗЛП выписывается по столбцам, значения базисных переменных берутся из строки c_j, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: = (0, 0, 0, 3, 4), = 0.

Данное решение не является оптимальным, поскольку решение не допустимое (не выполнено условие неотрицательности переменных), ему соответствуют отрицательные элементы в строке .

Над минимальным отрицательным элементом «4» в строке выбираем положительный, например «1», в строке x₄, следовательно, эта строка – разрешающая (выделена жирным шрифтом).

Находим максимальное отношение среди отношений элементов в строке целевой функции к соответствующим элементам разрешающей строки

.

Поскольку максимальное отношение соответствует первому столбцу, то – он разрешающий (выделен жирным шрифтом).

Разрешающий элемент «1» находится на пересечении разрешающей строки и разрешающего столбца.

Заполняем нижние части клеток. Под разрешающим элементом ставим «1». В разрешающей строке остальные элементы переписываем без изменения, а в разрешающем столбце остальные элементы записываем с противоположным знаком. Оставшиеся клетки заполняем по правилу прямоугольника:

клетка на пересечении первой строки и второго столбца:

1	2
«1»	1

21  11 = 1;

клетка на пересечении третьей строки и второго столбца:

«1»	1
2	1

11  21 = 1;

клетка на пересечении четвертой строки и второго столбца:

«1»	1
	
- 3	- 4

 41  (3)1 = 1;

клетка на пересечении первой строки и третьего столбца:

1		4
«1»		3

41  31 = 1;

клетка на пересечении третьей строки и третьего столбца:

«1»		3
2		8

81  32 = 2;

клетка на пересечении четвертой строки и третьего столбца:

«1»		3
		
- 3		0

01  3(3) = 9;

Таким образом, получаем следующую таблицу:

	yбаз	y4	y5
yсв	xсв xбаз	- x1	- x2	bi
y1	x3	1 1	2 1	4 1
y2	x4	«1» 1	1 1	3 3
y3	x5	2 2	1 1	8 2
cj		- 3 3	- 4 1	0 9

Переходим к следующей симплекс-таблице. При этом в базис включается пара переменных х₁, у₄, соответствующих разрешающему столбцу, а из базиса выводится пара переменных х₄, у₂, соответствующая разрешающей строке. В следующей таблице данные пары переменных меняются местами. Верхние части клеток заполняются элементами, полученными в результате деления соответствующих (стоящих на аналогичном месте) элементов из предыдущей таблицы в нижних частях клеток на разрешающий элемент «1»:

	yбаз	y2	y5
yсв	xсв xбаз	- x4	- x2	bi
y1	x3	1	1	1
y3	x1	1	1	3
y3	x5	2	1	2
cj		3	1	9

Решение ПЗЛП на втором шаге двойственного симплекс-метода также выписывается по строкам: = (3, 0, 1, 0, 2), = 9, решение ДЗЛП выписывается по столбцам: = (0, 3, 0, 0, 1), = 9. Данное решение также не оптимальное, поскольку еще остался отрицательный элемент «1». Необходим еще один шаг двойственного симплекс-метода.

Над отрицательным элементом «1» в строке выбираем положительный, предпочтительнее «1», в строке x₃, поскольку вторая строка была выбрана на предыдущем шаге метода, следовательно, первая строка – разрешающая (выделена жирным шрифтом).

Находим максимальное отношение среди отношений элементов в строке целевой функции к соответствующим элементам разрешающей строки

.

Поскольку максимальное отношение соответствует второму столбцу, то – он разрешающий (выделен жирным шрифтом).

Разрешающий элемент «1» находится на пересечении разрешающей строки и разрешающего столбца.

Заполняем нижние части клеток. Под разрешающим элементом ставим «1». В разрешающей строке остальные элементы переписываем без изменения, а в разрешающем столбце остальные элементы записываем с противоположным знаком. Оставшиеся клетки заполняем по правилу прямоугольника аналогично предыдущему шагу метода, получаем следующую таблицу:

	yбаз	y2	y5
yсв	xсв xбаз	- x4	- x2	bi
y1	x3	1 1	«1» 1	1 1
y3	x1	1 2	1 1	3 2
y3	x5	2 3	1 1	2 3
cj		3 2	1 1	9 10

Переходим к следующей симплекс-таблице. При этом в базис включается пара переменных х₂, у₅, соответствующих разрешающему столбцу, а из базиса выводится пара переменных х₃, у₂, соответствующая разрешающей строке. В следующей таблице данные пары переменных меняются местами. Клетки следующей таблицы заполняются элементами, полученными в результате деления соответствующих элементов из предыдущей таблицы в нижних частях клеток на разрешающий элемент «1». Поскольку в нижних частях клеток таблицы все элементы положительные и разрешающий элемент также положительный, то в следующей таблице будет получено оптимальное решение и нет необходимости делить на две части клетки в последней таблице:

	yбаз	y2	y1
yсв	xсв xбаз	- x4	- x3	bi
y5	x2	1	1	1
y3	x1	2	1	2
y3	x5	3	1	3
cj		2	1	10

Оптимальное решение ПЗЛП: = (2, 1, 0, 0, 3), = 10, оптимальное решение ДЗЛП: = (1, 2, 0, 0, 0), = 10.

Данное решение аналогично решению, полученному в соответствии с методом одновременного решения пары взаимо двойственных задач.