2.4.3. Оценка качества признаков
Для оценки качества
алгоритма выделения признаков, проводим
процедуру выделения признаков из
изображений обучающей выборки. Положим,
что N
– число классов, M
– число образцов класса в обучающей
выборке. Будем считать
- набор признаков дляm-го
элемента n-го
класса обучающей выборки (
).
Вычисляем среднее по выборке для каждого
признака каждого класса
:
.
(2.4)
Вычисляем дисперсию и среднеквадратичное отклонение (СКО):
,
(2.5)
,
(2.6)
Определяем минимальное расстояние от заданного класса до всех остальных по каждому признаку:
.
(2.7)
Качество
признака
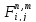определяется величиной СКО
,
и минимальной различающей способностью
признака, определяемым расстоянием
.
2.5. Классификация
В качестве классификатора были использованы: классификатор по минимальному евклидову расстоянию и двухслойный персептрон для признаков, полученных методом PCA. Классификация прямым сравнением признаков в случае анализа корреляционных данных.
2.5.1. Классификация по минимальному евклидову расстоянию
Алгоритмы классификации основаны на определении степени близости набора признаков рассматриваемого образа к каждому из классов. Правдоподобие получаемого результата зависит от выбранной метрики пространства признаков. К наиболее известным метрикам относится Евклидово расстояние:
(2.8)
где
- i-й признак из j-го эталонного вектора;
-
i-й признак тестируемого изображения
образа.
При классификации по методу ближайшего соседа символ будет отнесен к классу, вектор признаков которого наиболее близок к вектору признаков образа.
2.5.2. Классификация двухслойным персептроном
For the solution of the face detecting problem adapted a large quantity of neuron networks of different architectures, in particular - multilayer perceptrons. Example of the architecture of network - three-layered perceptron of the following form (Fig. 3):
ENTRANCE: vector
representation of signs (-1)
EXIT: expected result 1 or -1
Figure 3. Image of neural network
Merit of use neural networks for the solution of the faces detecting problem is the possibility of obtaining of classifier that well simulating complex function distribution of the faces images p(x | face).
Drawback of use neural networks is the need for thorough and tedious tuning to neural networks for obtaining the satisfactory result of classification.
Process of tuning the weights of network must lead to the minimization of mean-square error (1).
Algorithm of the presence of weights by the gradient descent:
1. We reduce to zero ΔW and ΔV (tuned weights).
2. We read input vectors X and calculate for them the answers Y.
3. We find the error signal (Y - T). If it is sufficiently small on all pairs of the training set, then we count the instruction of network in that in successfully finished, otherwise:
4. Is multiplied the error signal to derivatives by weights and add this to the future modification of weight ΔW and ΔV.
5. We add to the weights accumulated previously ΔW and ΔV, multiplied by η - velocity coefficient of instruction.
Observation: it is possible to still add here ΔW and ΔV, obtained on the previous iteration, after multiplying them on γ - coefficient of inertia. Then error will decrease more smoothly.
6. To pass to step (1).
It is provided also output from this cycle according to the number of iterations (if error does not diminish to the necessary value).
Вектор признаков, полученный методом PCA, представляющий собой набор собственных чисел, масштабировался в интервал [-0.5;0.5] диапазона допустимых входных значений персептрона. Масштабирование осуществлялось линейным преобразованием с учетом предполагаемого диапазона изменений значений собственных чисел [-fmax,fmax].