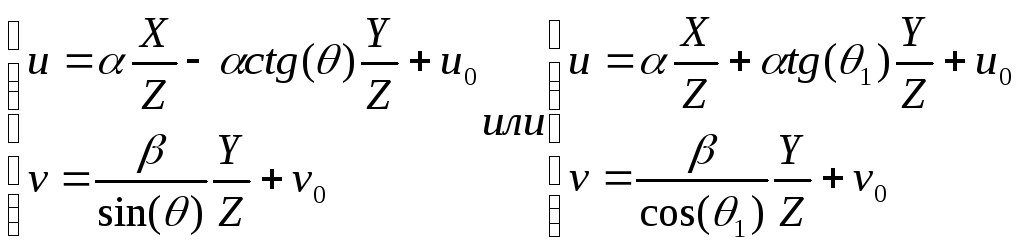1. Разработка алгоритмов и макета комплекса визуально-инерциальной навигации

   1. Сравнительный анализ алгоритмов одновременной локализации и построения карты припомощи телекамеры

Проведенный анализ алгоритмов одновременной локализации и построения трехмерной карты при помощи телекамеры в динамике показал, что к настоящему моменту основными недостатками существующих систем (в частности, системы Andrew J. Davison из Imperial College London и Javier Civera и J. M. M. Montiel из Университета Сарагосы) являются: нестабильная работа при совершении быстрых маневров, зависимость от устойчивой детектируемости визуальных признаков при работе в реальных условиях. В случае потери сопровождения визуальных признаков или при ошибочном сопровождении возможно накопление значительных ошибок в определении собственного местоположения. Опыт разработок ЦНИИ РТК в области инерциальной навигации показывает, что при совершении непродолжительных маневров можно достичь высокой точности определения собственных координат мобильного объекта с использованием БИНС. Системы спутниковой навигации могут быть эффективны при перемещении на больших расстояниях на открытой местности. В то же время, средства инерциальной навигации обладают известными недостатками, связанными с погрешностями, нарастающими во времени, а спутниковая навигация не всегда может быть доступна и обладает сравнительно высокой погрешностью при решении задач локальной навигации. В связи с этим актуальным является комплексирование средств визуальной навигации с системами инерциальной навигации, а также с другими источниками информации о движении, например, с одометрическими, ультразвуковыми датчиками и GPS.

1. Модель центральной перспективной проекции

   1. Описание модели

В качестве геометрической модели камеры очень часто используется модель центральной перспективной проекции. Эта модель соответствует идеальной камере-обскура.

В результате перспективной проекции возникает перевернутое изображение, поэтому вместо него удобно рассматривать виртуальное изображение, расположенное в плоскости, лежащей перед отверстием на таком же расстоянии, что и реальная плоскость изображения.

Модель перспективной проекции полностью описывается центром проекции и положением плоскости изображения. Поэтому проекция любой точки сцены на плоскость изображения может быть найдена как пересечение луча, соединяющего центр проекции и точку сцены, с плоскостью изображения.

Прямая линия, перпендикулярная плоскости изображения и проходящая через центр проекции называется оптической осью камеры, а точка пересечения оптической оси с плоскостью изображения – главной точкой.

2. Переход от системы координат камеры к системе координат изображения

Определим в трехмерном пространстве ортогональную систему координат O_CX_CY_CZ_C, начало которой совпадает с центром проекции, а осьZ_C с оптической осью камеры. Такая система координат называется стандартной системой координат камеры (Рисунок 1).

Пусть плоскость изображения находится на расстоянии fот оптического центра (fназывается фокусным расстоянием). Плоскость изображения, которая находится на единичном расстоянии от центра проекции и параллельна физической плоскости изображения, называется нормированной плоскостью изображения.

Рисунок 1 Системы координат

Пусть M– точка трехмерного пространства с координатами (X,Y,Z), которые заданы в системе координат камеры. Тогда проекцией точкиMна плоскость изображения является такая точкаmс координатами (x,y,z), которые также заданы в системе координат камеры, что:

Координаты точки mобычно выражаются в пикселях, а не в единицах, задающих координаты в стандартной системе координат камеры (см, мм). Поэтому для более полного описания камеры необходимо выразить координаты точек изображения в пикселях. При этом следует учесть тот факт, что пиксели обычно берутся прямоугольными, а не квадратными. Пусть- размеры пикселя в единицах стандартной системы координат камеры. Тогда координаты точкиmможно записать как:

В общем случае система координат oxyв плоскости изображения может быть не прямоугольной (вследствие некоторой производственной ошибки). Обозначим угол между осямиxиyза θ, а уголза θ₁.

Рисунок 2 Искажения СК изображения

Тогда координаты точки mв косоугольной системе координат будут иметь вид:

,

где y_­nиx_n– координаты точкиmв прямоугольной системе координат. Так как значениеy_nзадано в пикселях по осиY, то при вычислении значения координатыx, величинуy_nнеобходимо отмасштабировать, то есть пересчитать в пиксели по осиX.

Введем следующие обозначения: 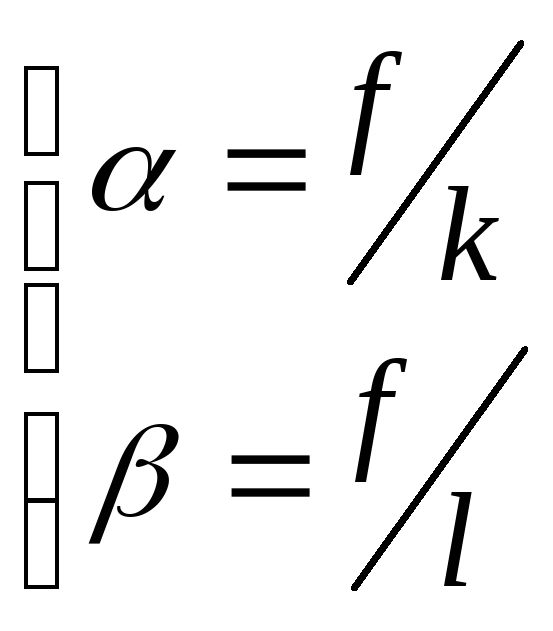, тогда система примет вид:

Эта формула может быть переписана в обозначениях угла θ как:

Как правило, начало системы координат в плоскости изображения находится в левом верхнем углу, а не в главной точке. Пусть (u₀,v₀) – координаты главной точки в системе координатUVв пикселях. Тогда координаты точкиmв этой системе координат примут вид: