Задача 1

Расчет основных параметров цилиндрической зубчатой передачи

Определить габариты цилиндрической прямозубой передачи (рис. 1.1) редуктора по контактным напряжениям σ_НР, возникающим при перекатывании зубьев колес, по исходным данным, представленным в таблице 1.1.

Таблица 1.1

Варианты заданий

Вариант	Мощность на валах передачи, кВт		Частота вращения, об/мин		Марка стали колес	Допускаемое напряжение σНР, МПа
			шестерни n1	колеса n2
	входной, Р1	выходной, Р2
1	5,0	4,5	1445	500	40	390
2	5,5	4,9	680	150	_	390
3	6,0	5,7	910	220	_	390
4	6,5	6,2	2840	700	_	390
5	7,0	6,6	1390	280	40Х	450
6	7,5	7,1	700	240	_	450
7	8,0	7,6	900	200	_	450
8	8,5	8,2	2880	650	_	450
9	9,0	8,5	1415	300	40ХН	490
10	9,5	9,0	675	225	_	490
11	10,0	9,5	955	190	_	490
12	4,5	4,0	2900	750	45	415
13	4,0	3,8	1465	390	_	415
14	3,5	3,3	720	200	_	415

Рис. 1.1. Кинематическая схема одноступенчатого цилиндрического редуктора: Р₁, Р₂ – мощности на ведущем и ведомом валах; Т₁ , Т₂ – вращающие моменты; n₁, n₂ – частоты вращения валов; z₁ , z₂ – числа зубьев шестерни и колеса соответственно; а_ω – межосевое расстояние.

ПРИМЕР расчета:

Рассчитать цилиндрическую прямозубую передачу редуктора сo следующими данными: мощность на валу колеса Р₂ = 4,2 кВт, частота вращения вала шестерни n₁ = 1465 об/мин, колеса n₂ = 390 об/мин, материалы соответственно сталь 40Х и сталь 45, допускаемое контактное напряжение σ_НР = 415 МПа.

Межосевое расстояние передачи при проектировочном расчете в соответствии с ГОСТ 21354-87 определяется по формуле:

,

где К_а – коэффициент, учитывающий влияние механических свойств материалов и формы сопряженных поверхностей зубьев в полюсе зацепления; для прямозубых передач К_а = 495;

u – передаточное число (см. формулу 1.1)

;

Т₂ – вращающий момент на валу колеса, Н·м,

;

где ω₂ – угловая скорость вала колеса, рад/с,

;
;

Р₂ – мощность на валу колеса, кВт;

Ψ_bа- коэффициент ширины колеса относительно межосевого расстояния (табл. 1.2.).

Значение коэффициента Ψ_bа при симметричном расположении колес можно принять любое из ряда стандартных значений: 0,315; 0,4; 0,5;

σ_НP – допускаемое контактное напряжение;

К_Нβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса (табл. 1.2).

Таблица 1.2

Значения коэффициентов

Ψßа	0,315	0,4	0,5
КНβ	1,02	1,035	1,05

.

Модуль передачи, мм,

m = (0,01...0,02)·аω;

m = (0,01...0,02)·112,7 = 1,12…2,25.

Значение модуля выбирается из ряда стандартных значений (табл. 1.3) и должно находиться в полученном интервале.

Таблица 1.3

Модули зубьев

Ряды	М о д у л ь, мм
1-й	1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25
2-й	1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22

Принимается m = 2 мм.

При выборе модуля следует учитывать, что величина его должна быть такой, чтобы выполнялось условие: z₁ ≥ z_min = 17.

Минимальное число зубьев шестерни для прямозубых передач z₁ = 17 установлено по условию отсутствия подрезания ножки зубьев при нарезании инструментом реечного типа.

Суммарное число зубьев

;
.

Полученное значение следует округлить до целого числа: z_с = 113.

Число зубьев шестерни

;
; z1 = 24.

Число зубьев колеса

z2 = zс – z1;
z2 = 113 – 24 = 89.

Фактическое передаточное число (см. формулу 1.1)

.

Отклонение от заданного передаточного числа (допускаемое отклонение 4 %):

.

Диаметры шестерни (1) и колеса (2), мм:

– делительный d1 = m ·z1; d2 = m · z2;
d1 = 2 ·24 = 48; d2 = 2 · 89 = 178;
– вершин зубьев d а1 = m · (z1 + 2); d а2 = m · (z2 + 2);
d а1 = 2 · (24 + 2) = 52; d а2 = 2 · (89 + 2) = 182;
– впадин зубьев d f1 = m · (z1 – 2,5); d f 2 = m · (z2 – 2,5);
d f1 = 2 · (24 – 2,5) = 43; d f 2 = 2 · (89 – 2,5) = 173.

Фактическое значение межосевого расстояния, мм

;
.

Ширина колеса, мм

b2 = Ψbа · аω;
b2 = 0,4 ·113 = 45,2.

Принимается b₂ = 45 мм.

Ширина шестерни, мм

b1 = b2 + m;
b1 = 45 + 2 = 47.

Полученное значение округляется до целого числа: b₁ = 47 мм.

Задача 2

Расчет основных параметров червячной передачи

Рассчитать межосевое расстояние а_ω червячного редуктора по контактным напряжениям σ_НР, возникающим в зоне зацепления червяка и червячного колеса, по исходным данным, представленным в таблице 2.1.

Определить модуль червячной передачи m, передаточное число u , число заходов червяка z₁ , диаметры (делительные, вершин и впадин), ширину венца червячного колеса b₂ и длину нарезанной части червяка b₁ (см. рис. 2.1).

Таблица 2.1

Варианты заданий

Вариант	Мощность на валу колеса Р2 , кВт	Частота вращения, об/мин.		Материал венца червячного колеса	Допускаемое напряжение σНР2, МПа
		червяка n1	колеса n2
1	1,5	2840	70	БрОФ 10-1	130
2	2,0	2810	80	БрОНФ	210
3	2,5	2850	60	БрОЦС 6-6-3	118
4	3,0	2880	65	БрОФ 10-1	190
5	3,5	2900	100	БрОЦС6-6-3	134
6	4,0	2940	90	БрОЦС6-6-3	165
7	4,5	2945	125	БрОФ 10-1	130
8	5,0	1470	100	БрОФ 10-1	190
9	5,5	1465	90	БрОНФ	210
10	6,0	1460	80	БрОЦС6-6-3	118
11	6,5	1445	100	БрОЦС6-6-3	134
12	7,0	1430	50	БрОЦС6-6-3	165
13	7,5	1435	60	БрОФ 10-1	130
14	8,0	14I5	70	БрОНФ	210

ПРИМЕР расчета:

Рассчитать червячную передачу редуктора по следующим данным: мощность на валу червячного колеса P₂ = 3 кВт; n₂ = 100 об/мин; n₁ = 1450 об/мин; нагрузка постоянная, передача нереверсивная, срок службы не ограничен. Материалы: для червячного колеса (венца) – бронза БрОФ 10-1 (литье в кокиль), для которой σ_НР2 = 190 МПа; для червяка – сталь 45, термообработка – закалка ТВЧ при твердости менее НRС 45.

Межосевое расстояние, мм ;
Рис. 2.1. Геометрические параметры червяка и червячного колеса

Передаточное отношение

;
.

Число заходов червяка z₁ выбирается из таблицы 2.2 в зависимости от передаточного отношения.

Таблица 2.2

Рекомендуемые значения z₁

Передаточное отношение u	7 – 13	14 – 27	≥ 28
Число заходов червяка z1	4	2	1

Принимаем z₁ = 2.

Коэффициент полезного действия передачи η_ч.п (табл. 2.3) зависит от числа заходов червяка.

Таблица 2.3

Значения КПД червячных передач

Число заходов червяка z1	1	2	4
КПД передачи ηч.п	0,65 – 0,7	0,7 – 0,75	0,85 – 0.9

Принимаем η_ч.п = 0,75.

Вращающий момент на валу колеса, Н·м,

;
.

Угловая скорость червячного колеса, рад/с,

;
.

Ориентировочное значение скорости скольжения, м/с.

,

где Р₁ – мощность на валу червяка_, кВт,

;
.

где η_.п – КПД одной пары подшипников качения (η_.п = 0,99 – 0,995).

.

Коэффициент нагрузки

,

где К _β – коэффициент концентрации нагрузи (при постоянной нагрузке К _β = 1);

К _ν – динамический коэффициент, зависящий от скорости скольжения и качества изготовления передачи (табл. 2.4).

Таблица 2.4

Значения коэффициента К _ν

Степень точности	Скорость скольжения, м/с
	до 1,5	свыше 1,5 до 3	свыше 3 до 7,5
8	1,1 – 1,2	1,2 – 1,3	1,4

Примечание. 8-я степень точности назначается для смазываемых передач закрытого типа с механическим приводом.

.

Число зубьев колеса

;
.
.

Число зубьев колеса z₂ следует округлять до целого.

Коэффициент диаметра червяка q рекомендуется принять:

;
.

Значение q округляем до стандартного значения (табл. 2.5): q = 8.

Таблица 2.5

Коэффициент диаметра червяка q (ГОСТ 19672-74)

1-й ряд	6,3		8		10		12,5		16		20		25
2-й ряд	-	7,1		9		11,2		14		18		22,4		-

Примечание. Допускается принимать q = 7,5 и 12.

Межосевое расстояние, мм

;
.

Модуль передачи, мм

;
.

Значение модуля следует принять ближайшее стандартное (табл. 2.6): .

Таблица 2.6

Модули червячной передачи (ГОСТ 19672-74)

1-й ряд	2,5		3,15		4	5	6,3		8	10	12,5	16	20
2-й ряд	-	3		3,5		6		7		12		-	-

Диаметр делительный червяка, мм

;
.

Диаметр вершин витков, мм

;
.

Диаметр впадин, мм

;
.

Диаметр делительной окружности колеса, мм

;
.

Диаметр окружности вершин зубьев, мм

;
.

Диаметр колеса наибольший, мм

;
.

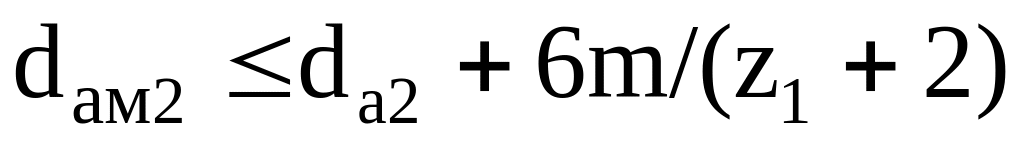Диаметр впадин, мм

Длина нарезанной части червяка, мм

, при и
, при
.

Значение b₁ округляется до целого числа: мм.

Ширина венца колеса, мм

, при и
, при
.

Значение b₂ округляется до целого числа: мм.

Фактическое межосевое расстояние, мм

;
.

Задача 3

Зная частоты вращения входного n₁ и выходного n₂ валов коническо-цилиндрического редуктора и числа зубьев конических шестерни и колеса (z₁ и z₂ соответственно) определить передаточные числа редуктора u и каждой из ступеней передачи (конической u_к и цилиндрической u_ц).

Варианты заданий

Вариант	Частоты вращения валов, об/мин		Числа зубьев
	входного n1	выходного n3		шестерни z1	колеса z2
1	2945	53		21	160
2	950	36		24	154
3	1435	57		27	140
4	700	35		22	170
5	2940	65		28	186
6	900	45		32	140
7	975	30		25	138
8	680	26		29	122
9	1455	29		33	150
10	730	24		35	166
11	965	38		20	174
12	1445	36		23	142
13	2850	71		27	162
14	1455	36		24	183
15	970	32		28	157
16	730	34		30	163
17	1460	36		34	194
18	975	34		31	180
19	730	36		29	185
20	1460	48		18	144