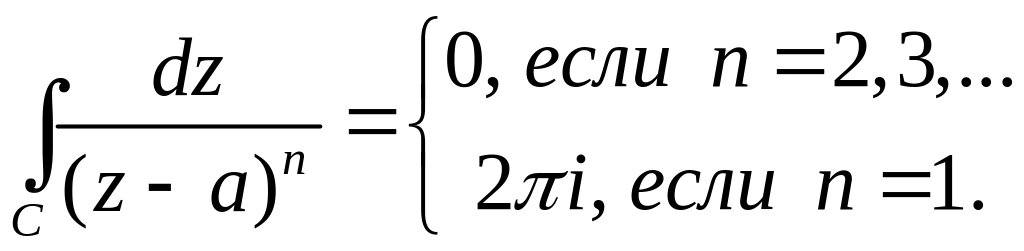Задания для самостоятельной работы

Вычислить следующие интегралы:

1. , если путь интегрирования представляет собой

а) прямолинейный отрезок, соединяющий точки и ;

б) ломаную , где .

2. , если путь интегрирования представляет собой

а) прямолинейный отрезок, соединяющий точку с точкой ;

б) полуокружность единичного радиуса с центром в начале координат, лежащая в верхней полуплоскости, причем началом интегрирования является точка ;

в) окружность (обход против часовой стрелки).

3. Вычислить , где – дуга окружности , . Ответ: .

4. Оценить по модулю интеграл , где , (начало

интегрирования в точке ). Ответ: .

§7. Интегральная теорема коши. Формула коши

Интеграл от аналитической функции обладает замечательным свойством, сформулированным в тереме Коши.

Теорема Коши. Если – однозначная аналитическая функция в односвязной области , то интеграл от этой функции по любому замкнутому контуру равен нулю:

(1)

Другими словами, интеграл от однозначной аналитической функции в односвязной области не зависит от пути интегрирования.

Пример 1. Интеграл по любой замкнутой кривой , так как функция является аналитической на всей комплексной плоскости. ☻

Задача 1. Дана функция . Можно ли применить теорему Коши к интегралу , если а) б) в) . Ответ аргументируйте. Ответ: 1) можно; 2) нельзя; 3) нельзя.

В качестве положительного направления обхода замкнутого контура принимается направление, при котором область, ограниченная этим контуром, остается слева. Так, если контур представляет собой окружность , то (против часовой стрелки) есть граница круга , а (по часовой стрелке) есть граница внешности круга, то есть области .

В случае многосвязной области (рис.1) ее полная граница состоит из внешнего контура и внутренних контуров . При положительном направлении обхода полной границы область все время остается слева, т. е. внешний контур обходится против часовой стрелки, а каждый внутренний – по часовой стрелке.

Рис.1

Теорема Коши для многосвязной области. Пусть – аналитическая функция в многосвязной области с полной границей и непрерывна в замкнутой области . Тогда интеграл от функции по полной границе области равен нулю (обход границы совершается в положительном направлении):

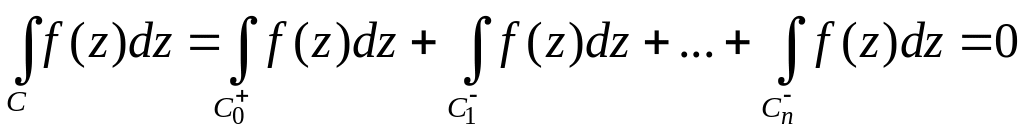(2)

Формулу (2) можно переписать в виде

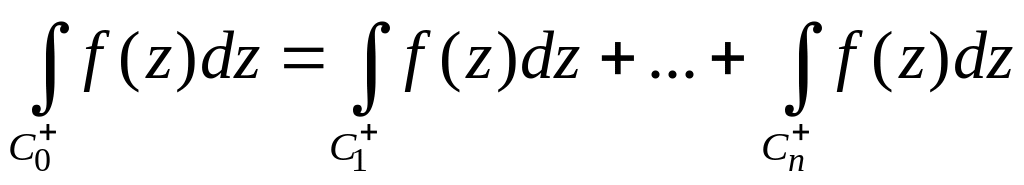(3)

З начит, интеграл от функции по внешнему контуру равен сумме интегралов по внутренним контурам (каждый из контуров обходится против часовой стрелки).

В частности, пусть функция является аналитической на контурах , и в двухсвязной области , ограниченной этими Рис.2

контурами (рис.2). Тогда из (3) получаем

. (4)

В этом случае интеграл независимо от формы кривой интегрирования сохраняет постоянное значение.

Пример 2. Показать, что если произвольный замкнутый контур, не проходящий через точку , и – целое число, то

Решение. При подынтегральная функция является аналитической и интеграл равен нулю в силу теоремы Коши (независимо от взаимного расположения точки и контура ).

При подынтегральная функция имеет вид , где Пусть точка находится вне контура , тогда функция является аналитической внутри этого контура. И в этом случае справедлива теорема Коши – интеграл равен нулю.

Осталось рассмотреть интеграл 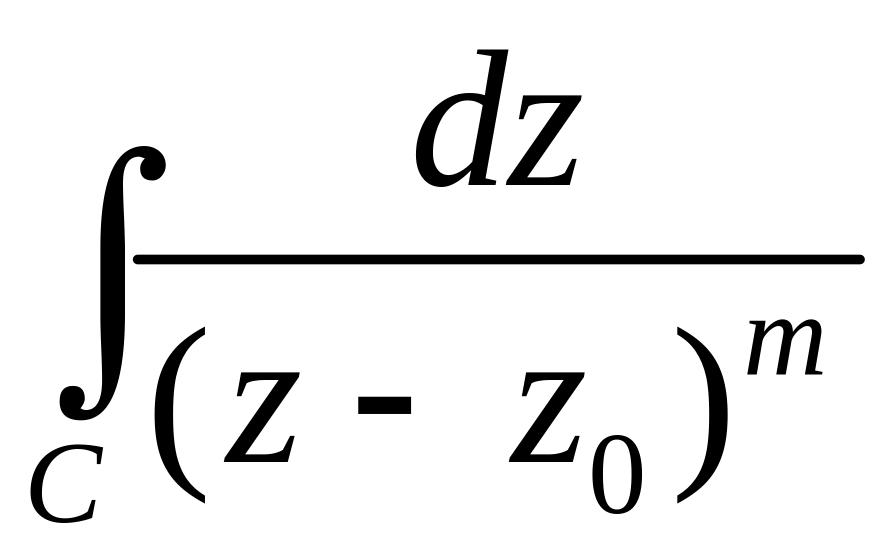, когда точка находится внутри контура , то есть в точке нарушается аналитичность подынтегральной функции. Выбросим из области круг , граница которого лежит внутри контура . Функция аналитична и на контуре , и на окружности , а также в двухсвязной области, ограниченной этими контурами. Значит, интеграл в силу формулы (1) сохраняет постоянное значение, которое можно найти, принимая за контур интегрирования окружность : .

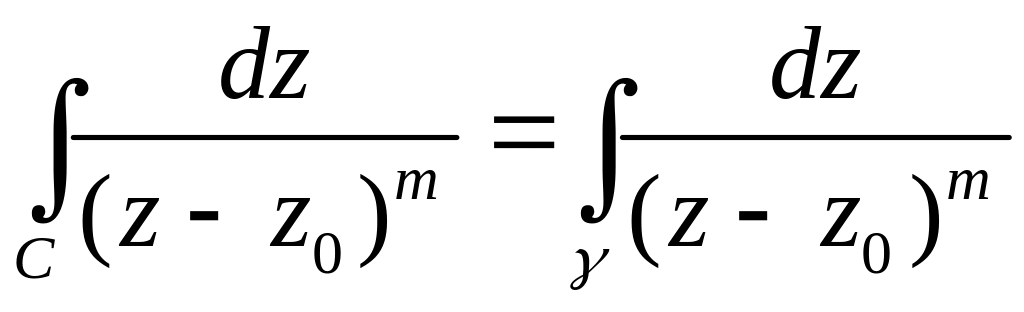В примере 3 предыдущего параграфа было показано, что такой интеграл не зависит ни от радиуса окружности, ни от точки , интеграл равен нулю при и равен при . Все возможные случаи исчерпаны. ☻

Аналитичность функции налагает на нее такие жесткие условия, что информации о поведении функции на некоторой замкнутой кривой в области аналитичности достаточно, чтобы определить значение функции в любой внутренней точке области – этот факт отражен в интегральной формуле Коши.

Интегральная формула Коши

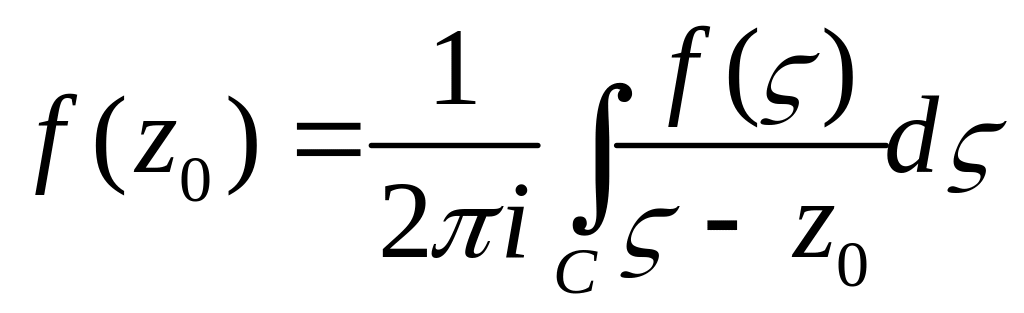(5)

позволяет вычислить значение функции в любой точке области ее аналитичности , если известны значения этой функции на контуре , целиком лежащем в и содержащем внутри себя точку .

Интеграл, стоящий справа в формуле Коши, называется интегралом Коши. В подынтегральном выражении первый множитель – это плотность интеграла Коши (значение на контуре функции , аналитической всюду в , во всяком случае, непрерывной на контуре ). Второй множитель 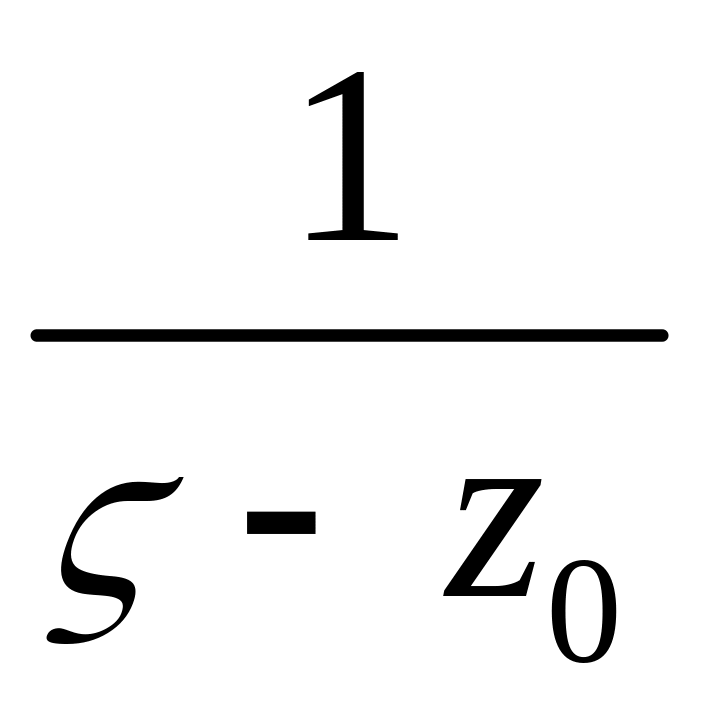– это ядро интеграла Коши (значение на контуре функции , которая теряет аналитичность в точке , если и является аналитической всюду в , если точка находится вне контура ).

Значит, интеграл Коши равен

(6)

Заметим, что в задачах обычно не подчеркивается разница между переменной интегрирования и точкой .

Пример 3. Вычислить интеграл , где контур .

Решение. Подынтегральная функция имеет две особые точки: и . Первая из них лежит внутри заданного контура интегрирования, а вторая – вне его. Представим интеграл в виде

.

Здесь в подынтегральной функции множитель представля-

ет собой аналитическую внутри контура и на нем функцию – это плотность интеграла Коши. Множитель – ядро интеграла Коши (аналитичность нарушается во внутренней точке ). Согласно формуле (6)

. ☻

Задача 2. Вычислить интеграл , если а) точка лежит внутри контура , а точка вне его; б) точка лежит внутри контура , а точка вне его; в) обе особые точки лежат вне контура . Ответ: а) б) в) 0.

Пример 4. Вычислить интеграл , если контур .

Решение. Подынтегральная функция имеет две особые точки и , причем обе они лежат внутри заданного контура . Непосредственно формулу (6) применить нельзя.

1 способ. Представим дробь в виде суммы элементарных дробей и воспользуемся линейным свойством интеграла:

Плотность каждого из полученных интегралов Коши , ядро первого интеграла , ; второго – , . Значит, . Тогда

.

2 способ. Проведем произвольно линию между точками и , разделяющую область на части и (рис.3) так, что , . При этом контур разбивается на части и . Область с границей содержит внутри единственную особую точку , значит,

.

Область с границей содержит единственную особую точку , значит,

.

Складываем оба результата. С учетом аддитивности интеграла получаем

.

Но интегралы по и по взаимно уничтожаются, поэтому

.☻

Задача 3. Вычислить интеграл , если обе особые точки и лежат внутри контура . Ответ: 0.

Если контур представляет собой окружность радиуса с центром в точке , ( ), то замена позволяет получить из формулы Коши теорему о среднем:

.

То есть значение аналитической функции в центре круга равно среднему арифметическому из ее значений на окружности этого круга.

Из аналитичности функции в точке , то есть из существования ее первой производной в некоторой окрестности этой точки, и интегральной формулы Коши следует существование в окрестности той же точки производных любого порядка данной функции, причем

(7)

Пример 5. Вычислить интеграл , если – замкнутый контур, обходящий точку .

Решение. Положим в формуле (3) , тогда

.

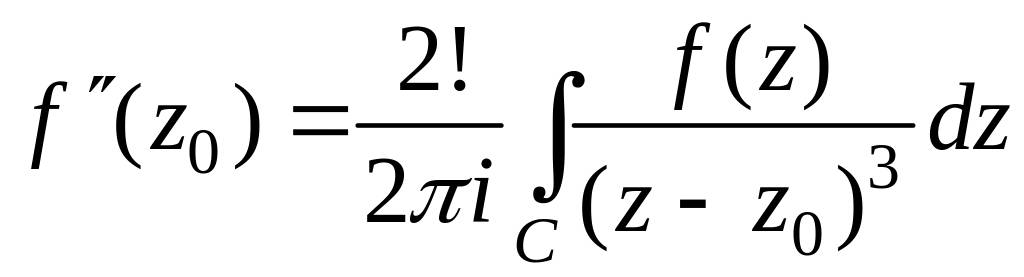Сопоставляя с заданным интегралом, видим, что и , т.е.

☻.

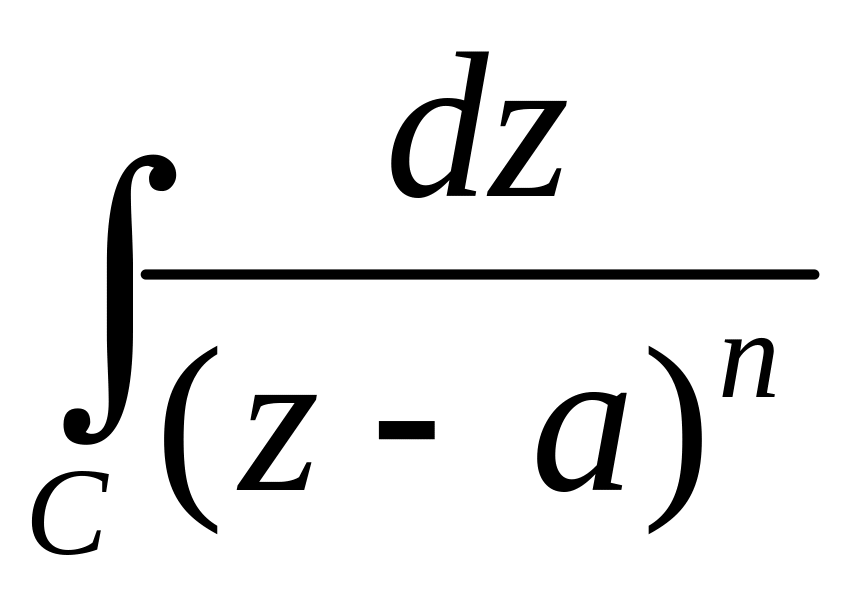
Задача 4. Вычислить интеграл , если – замкнутый контур, содержащий внутри точку (воспользоваться формулой (7)). Сравнить результат с примером 2. Ответ: