Задания для самостоятельной работы

1. Найти действительную и мнимую части следующих функций

1) ; 2) ; 3) .

2. Найти модули и главные значения аргументов комплексных чисел

1) ; 2) ; 3) ; 4) ; 5) .

3. Пусть . Доказать, что

1) ; 2) ; 3) .

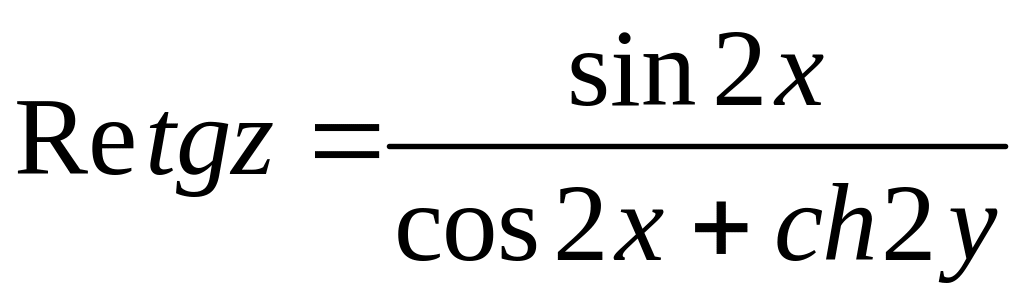4. Выделить действительную и мнимую части следующих функций

1) ; 2) ; 3) ; 4) .

5. Найти действительную и мнимую части следующих значений функций

1) ; 2) ; 3) ;

4) ; 5) , ; 6) , ;

7) ; 8) ; 9) ; .

6. Найти все значения следующих степеней

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

7. Записать в алгебраической форме числа

1) ; 2) ; 3) ; 4) ; 5) .

§4.Предел функции комплексной переменной. Непрерывность

Пусть однозначная функция комплексной переменной определена в области .

Определение. Число называется предельным значением функции в точке , , если можно указать такое , , что для всех точек , удовлетворяющих условию , имеет место неравенство .

Пример 1. Найти .

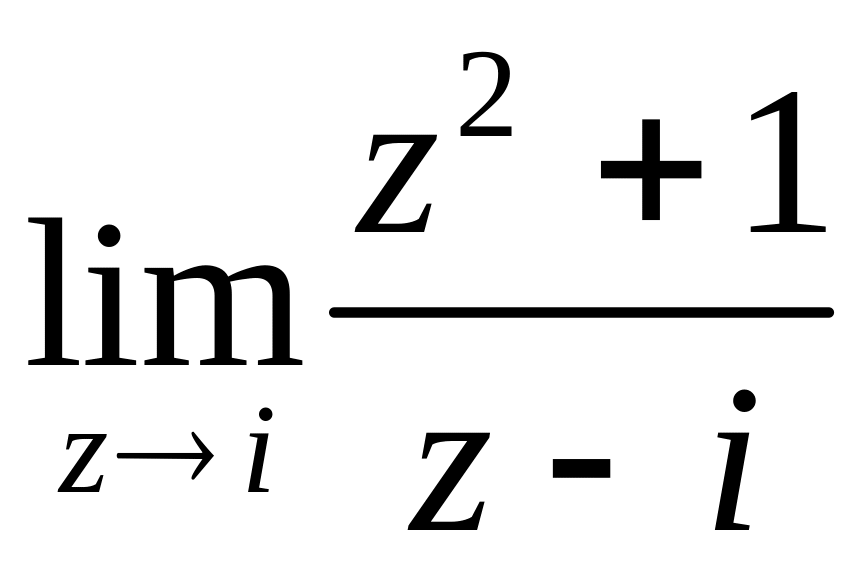Решение. . ☻

Определение. Функция непрерывна в точке , если предельное значение этой функции в точке существует и совпадает с частным значением функции в этой точке, то есть .

Иначе: функция непрерывна в точке , если можно указать такое , , что для всех точек , удовлетворяющих условию , имеет место неравенство .

Функция, непрерывная в каждой точке области , называется непрерывной в этой области. Точкой разрыва функции называется точка, в которой нарушается непрерывность.

Пример 2. Функция непрерывна на всей комплексной плоскости; функция имеет две точки разрыва ; функция терпит разрыв в точках . ☻

Непрерывность функции равносильна непрерывности двух действительных функций и .

Определение. Функция равномерно непрерывна в области , если можно указать такое , , что для любых двух точек , расстояние между которыми меньше : , расстояние между соответствующими значениями функции меньше : .

Пример 3. Функция непрерывна в круге и равномерно непрерывна в замкнутом круге , где , то есть в круге радиуса немного меньше единицы. ☻

Задания для самостоятельной работы

Найти 1) ; 2) ; 3) ; 4) .

§5. Дифференцирование функций комплексной переменной. Условия коши-римана.

Пусть функция комплексной переменной определена в области , и пусть точки и принадлежат области . Обозначим

.

Определение. Функция называется дифференцируемой в точке , если существует предел разностного отношения при стремлении к нулю произвольным образом. Этот предел называется производной функции в точке и обозначается символом , то есть

.

Пример 1. Убедиться, что функция не дифференцируема ни в одной точке комплексной плоскости.

Решение. Имеем . Составим разностное отношение

.

Покажем, что предел отношения зависит от способа стремления к нулю. Действительно, при стремлении к нулю вдоль линии, параллельной действительной оси, имеем , и . А при стремлении к нулю вдоль линии, параллельной мнимой оси, имеем , и 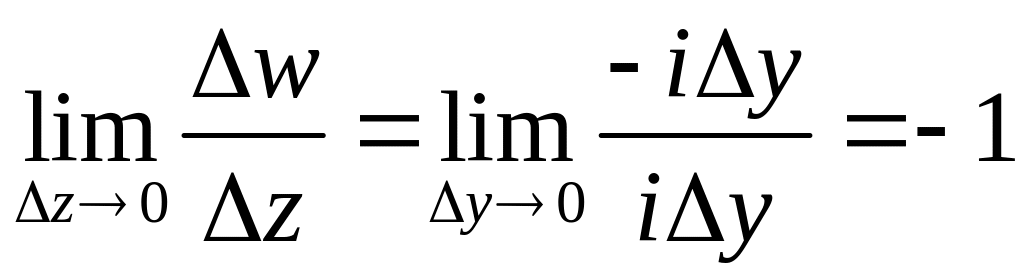. Значит, при стремлении к нулю произвольным образом предел отношения , а с ним и производная функции не существует ни в одной точке. ☻

Требование дифференцируемости функции комплексной переменной в точке налагает определенные условия на поведение действительной и мнимой частей этой функции в окрестности точки . Имеют место следующие утверждения:

1. Если функция дифференцируема в точке , то в точке существуют частные производные функций и по переменным , причем выполняются соотношения (условия Коши-Римана)

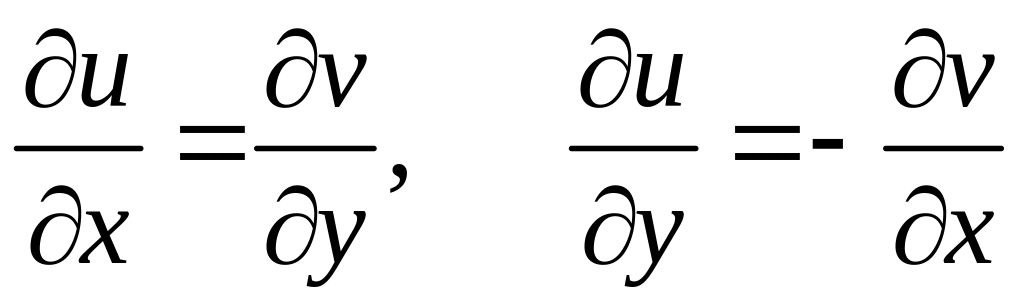. (К.-Р.)

2. Если в точке функции и дифференцируемы, а их частные производные связаны условиями К.-Р., то функция является дифференцируемой функцией комплексной переменной в точке .

Определение. Если функция дифференцируема во всех точках области , то она называется аналитической в области .

Необходимым и достаточным условием аналитичности функции в области является существование в этой области непрерывных частных производных функций и , связанных соотношениями К.-Р.

Производная аналитической функции представляется одной из следующих формул:

; ; ; .(*)

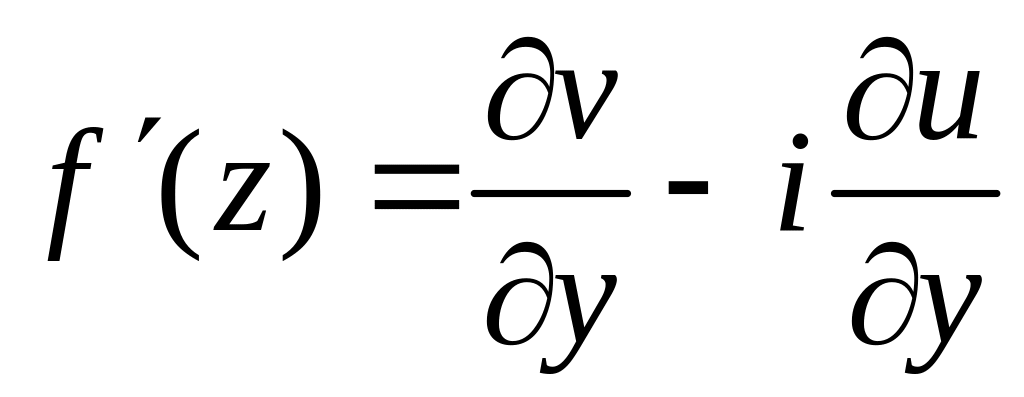Известные правила дифференцирования суммы, разности, произведения, частного, степени, сложной и обратной функции остаются справедливыми и в случае комплексного аргумента.

Пример 2. Показать, что функция является аналитической на всей комплексной плоскости. Найти производную этой функции.

Решение. Представим заданную функцию в виде . Имеем

.

Функции как функции действительных переменных имеют непрерывные частные производные в любой точке . Вычисляем ; .

Условия К.-Р. выполняются. Следовательно, функция является аналитической на всей комплексной плоскости. Производную найдем, например, по первой из четырех формул (*):

.

Определение. Функция называется аналитической в точке , если она дифференцируема как в самой точке , так и в некоторой ее окрестности. Иначе, аналитичность функции в точке означает ее аналитичность в некоторой окрестности этой точки.

Пример 3. Может ли функция быть аналитической хотя бы в одной точке комплексной плоскости?

Решение. Выделим действительную и мнимую части заданной функции:

.

Значит, . Функции и имеют непрерывные производные в любой точке , но условия К.-Р. 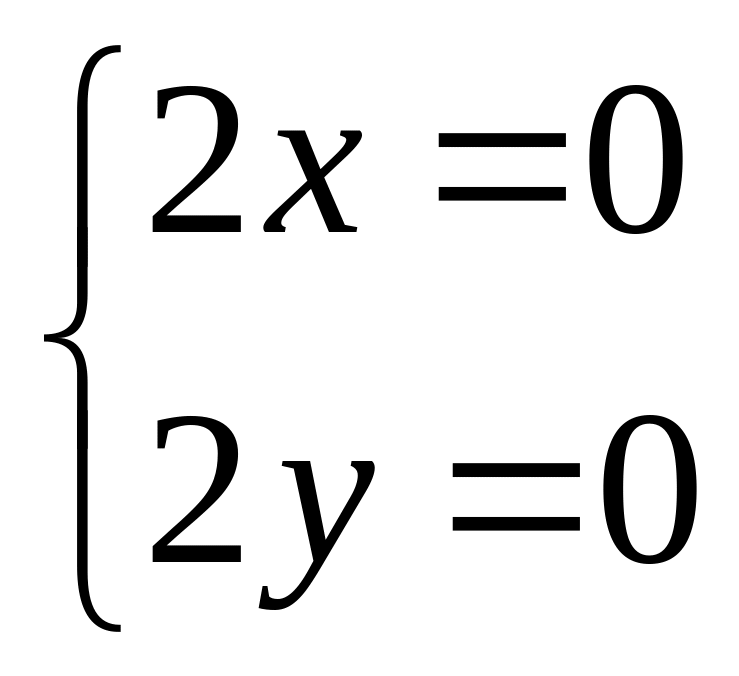выполняются только в точке . Следовательно, функция дифференцируема только в точке , поэтому не может быть аналитической даже в этой точке. ☻

Точки плоскости, в которых однозначная функция является аналитической, называют правильными точками этой функции, а точки, в которых функция не является аналитической (в частности, точки, в которых функция не определена), – особыми точками.

Определение. Функция называется гармонической в области , если она всюду в области имеет непрерывные частные производные первого и второго порядков и удовлетворяет уравнению Лапласа .

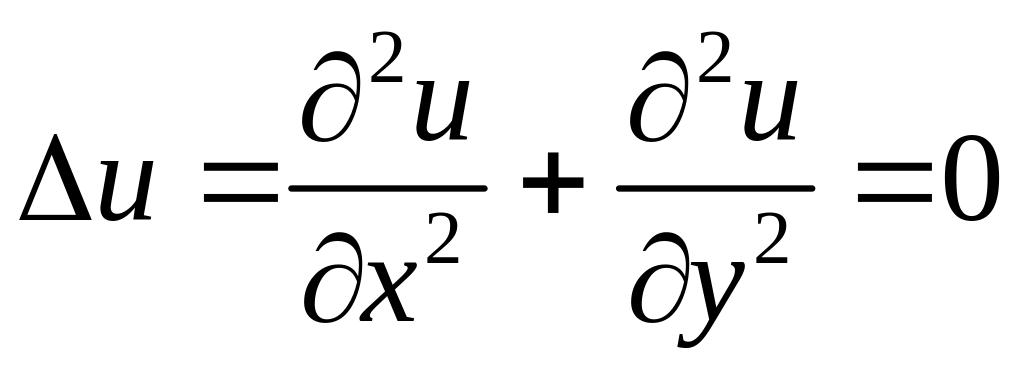Пример 4. Показать, что функция является гармонической.

Решение. Находим

☻

Задача 1. Убедиться, что действительная и мнимая части аналитической функции являются гармоническими функциями.

Определение. Две гармонические функции, удовлетворяющие условиям Коши-Римана, называются сопряженными гармоническими функциями.

Пример 5. Даны функции , . Являются ли они сопряженными гармоническими функциями?

Решение. Очевидно, что функции и гармонические. Проверим условия К.-Р.:

.

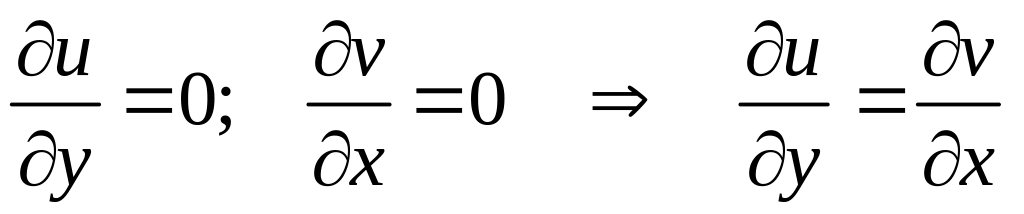
Видим, что одно из этих условий не выполнено. Значит, и не являются сопряженными гармоническими функциями. ☻

Пример 6. Дана функция . Можно ли принять ее за действительную часть аналитической функции? Если да, то какой именно?

Решение. Легко проверить, что данная функция удовлетворяет уравнению Лапласа. Значит, ее можно принять за действительную часть некоторой аналитической функции . Найдем ; 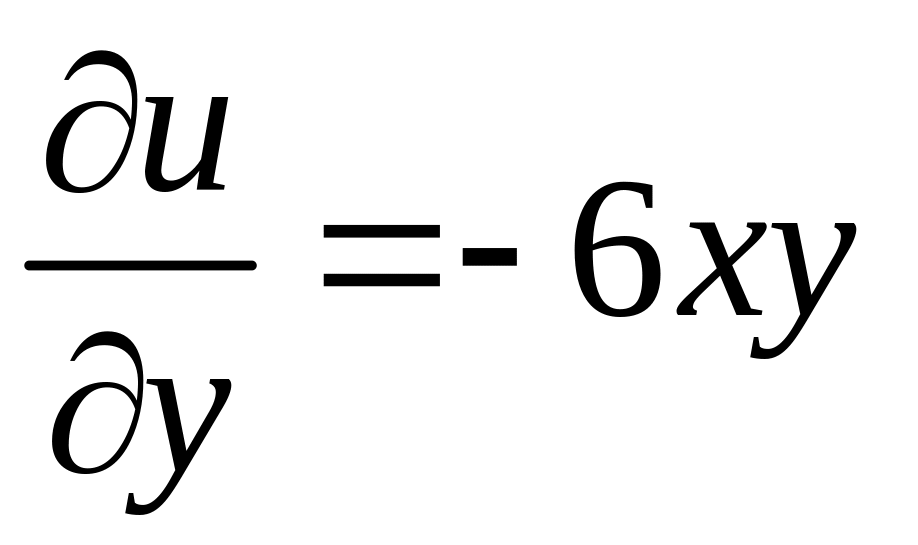. Подставляя эти производные в условия Коши-Римана, получим ; . Первое соотношение дает

(вместо постоянной появляется произвольная функция от переменной , по которой не производилось интегрирование). Значит, . Для определения неизвестной функции дифференцируем по : и сравниваем со вторым соотношением: . Отсюда заключаем, что . Значит, . Окончательно,

. ☻