
Лекции / ЛЕКЦИЯ8_09
.pdf
8 ПЕРЕХОДНЫЕ ПРОЦЕССЫ ВО ВРЕМЕННОЙ ОБЛАСТИ. АНАЛИЗ УСТАНОВИВШЕГОСЯ РЕЖИМА В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА.
ОПЕРАТОРНЫЙ МЕТОД ДЛЯ РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
8.1 Переходные процессы во временной области
В реальной действительности условия стационарных процессов в цепях никогда не выполняются. Любое непериодическое изменение вида воздействия
или изменение параметров цепи приводит к нарушению стационарности - ре
жима.
Рассмотрим с качественной точки зрения явления, возникающие в линей-
ных цепях при переходе от одного стационарного состояния к другому.
При наличии реактивных(энергоёмких) элементов переход цепи к новому стационарному состоянию сопровождается появлением так называемых пере-
ходных процессов.
Эти процессы – частный случай более общих неустановившихся (нестацио-
нарных) процессов, возникающих при произвольном непериодическом воздейст-
вии, а также при произвольном непериодическом изменении параметров цепи.
Это связано с особенностями изменения энергии электромагнитного поля в реактивных элементах: энергия поля в индуктивностях и емкостях не может
меняться мгновенно.
Первый закон коммутации: потокосцепление и ток через индуктивность не
могут измениться скачком, их значение в первый момент после коммутации равно их значению в последний момент перед коммутацией.
Второй закон коммутации: заряд и напряжение на емкости не могут изме-
ниться скачком, их значение в первый момент после коммутации равно их зна-
чению в последний момент перед коммутацией.

Изменение энергии за единицу времени представляет собой мощность, от-
даваемую или потребляемую соответствующим элементом:
dW |
= p . |
() |
|
||
dt |
|
|
Классическая теория электричества (в отличие от квантовой теории) не до-
пускает, что энергия меняется скачком – так как при этом производная обраща-
ется в бесконечность, и мощность принимает бесконечно большое значение.
То есть, в цепи с реактивными элементами величины, определяющие запас энергии, при переходе к новому стационарному состоянию должны меняться во времени плавно, без скачков. То есть, выходной ток или напряжение будут от-
личаться по форме от внешнего воздействия.
Теоретически переходные процессы имеют бесконечно большую продол-
жительность. В действительности значения напряжения и тока в цепи по ис-
течении конечных промежутков времени становятся близкими к установив-
шимся значениям.
Анализ процессов в линейной цепи основан на решении уравнений Кирх-
гофа для мгновенных напряжений и токов на элементах. Они сводятся к линей-
ному неоднородному дифференциальному уравнению с постоянными коэффици-
ентами.
При расчёте отклика в переходном режиме необходимо вводить начальные
условия.
Различают независимые и зависимые начальные условия.
Независимые начальные условия– это значения токов в индуктивностях iL(0–) и напряжений на емкостях uС (0–), которые определяются исходя из законов коммутации, для схемы до коммутации при t = 0–.

Зависимые начальные условия – это все остальные токи и напряжения в
схеме, которые определяются из расчета схемы после коммутациипри t = 0+
при уже известных независимых начальных условиях – iL(0–) и uС (0–).
При расчете зависимых начальных условийиндуктивность заменяют ис-
точником постоянного тока IL = iL(0–) = iL(0+), направление которого совпадает с направлением тока iL.
Ёмкость заменяется источником постоян
ЕС = uС(0–) = uС(0+), направление которой противоположно току заряда емко-
сти iС.
Для определения независимых и зависимых начальных условий можно исполь-
зовать любой известный метод расчета(метод контурных токов, узловых потенциа-
лов, принцип наложения, законы Кирхгофа).
Вынужденные составляющие напряжения и тока – это их значения в устано-
вившемся режиме после коммутации. Рассчитываются в схеме после коммутации
любым методом.
Для расчёта переходных процессов наиболее часто используют классический
метод решения дифференциальных уравнений с постоянными коэффициента-
ми.
Решение ищут в виде суммы двух функций:
y(t) = y1(t) + y2(t),
где y1 – частное решение исходного уравнения;
y2 – общий интеграл однородного дифференциального уравнения.
Функция y1(t), удовлетворяющая дифференциальному уравнению с правой ча-
стью, непосредственно зависит от внешнего воздействия, то есть представляет
собой ВЫНУЖДЕННЫЙ режим, задаваемый в цепи внешним источником.

Общее решение однородного дифференциального уравнения, т. е. функция y2(t), характеризует явления, обусловленные изменением начального энергети-
ческого состояния цепи в отсутствие вынужденного воздействия. Эти явления
называют собственными или СВОБОДНЫМИ процессами.
То есть, переходной процесс представляет собой совокупность свободной и вынужденной составляющих токов и напряжений, которые должны быть связа-
ны между собой посредством начальных условий.
Начальный запас энергии в реактивных элементах всегда ограничен, и при наличии потерь собственные процессы с течением времени затухают, и при t
® ¥ в цепи будет только вынужденный режим.
8.2 Классический метод расчета переходных
в цепях синусоидального тока (линейных цепях первого порядка)
Цепь первого порядка это цепь, которая после коммутации содержит одну емкость или одну индуктивность, характеризуется дифференциальным уравне-
нием первого порядка и имеет один корень характеристического уравнения.
Рассмотрим расчет переходного процесса в таких цепях на конкретном приме-
ре. Значительный практический интерес представляют нестационарные явления во
времени, например, возникающие при заряде и разряде емкости.
Предположим, что цепь на рисунке 8.1 в момент t = 0 подключается к источ-
нику внешнего напряжения. Напишем для этой цепи второй закон Кирхгофа:
uС + ur = e(t), t ³ 0. |
() |

r

 C e(t)
C e(t)
Рисунок 8.1 – Заряд ёмкости через сопротивление
Учитывая, что ток в цепи i = C |
duC |
и ur = ir = rC |
duC |
, будем иметь: |
||
dt |
|
|||||
|
|
|
|
dt |
||
rC |
duC |
+ uС = e(t), |
() |
|||
|
||||||
|
dt |
|
|
|
||
или:
duc |
+ |
1 |
uc |
= |
1 |
e(t ) |
|
|
|
|
|
. |
() |
||||
dt rC |
|
rC |
||||||
Полученное равенство представляет собойлинейное дифференциальное
уравнение первого порядка с неизвестной функцией uС.
Общее решение уравнения можно записать в виде суммы СВОБОДНОЙ uСВ и
ВЫНУЖДЕННОЙ иВ составляющих напряжения:
- |
t |
|
|
t Ц + uВ , |
|
||
uC = uСВ + uВ = Ae |
(А) |
||
где tЦ = rC – постоянная времени цепи rС.
Рассмотрим некоторые примеры переходных процессов приpaзличных
формах внешнего воздействия.

ВКЛЮЧЕНИЕ В ЦЕПЬ rС ПОСТОЯННОГО НАПРЯЖЕНИЯ (заряд емко-
сти через сопротивление).
Если цепь rС подключается к источнику постоянного напряженияUО,
функция е(t) имеет вид скачка напряжения.
Величина иВ в этом случае должна быть равна внешнему напряжению UО,
так как при t ® µ емкость заряжается до напряжения источника питания.
Следовательно,
- |
t |
|
|
|
t Ц |
|
|||
uC = U0 + Ae |
() |
|||
. |
||||
Для определения постоянной интегрированияА введем начальные усло-
вия.
Так как значение энергии, запасённой конденсатором не может изменяться во времени скачками, то напряжение на ёмкости при любом конечном измене-
нии воздействия должно изменяться во времени непрерывным образом. Поэтому
можно утверждать, что напряжение на емкости при скачкообразном изменении внешнего воздействия от НУЛЯ до U0 остается неизменным.
Всоответствии с этим будем иметь uС(0+) = uС(0–) = 0, откуда вытекает, что
А= –U0.
Таким образом, при t ³ 0:
|
|
|
- |
t |
|
|
|
- |
t |
|
|
|
|
|
t Ц ; |
|
|
t Ц ) . |
|
||||
u |
= -U |
0 |
e |
u = U |
0 |
( 1 - e |
( ) |
||||
СВ |
|
|
|
|
С |
|
|
|
|
||
Из последнего выражения видно, что напряжение на ёмкости в процессе
заряда возрастает по экспоненциальному закону, стремясь к величине U0 (ри-
сунок 8.2).

u |
|
U0 |
uC |
|
|
|
ur |
0 |
t |
|
uCВ |
–U0 |
|
Рисунок 8.2 – Переходной процесс в rC цепи при включении постоянного на-
пряжения
Скорость заряда емкости зависит от постоянной временя цепи: чем больше величина емкости и активного,
определяющих tЦ, тем медленнее растет напряжение uС.
Ток
|
du |
|
CU |
|
|
- |
t |
|
U |
|
|
- |
t |
|
|
|
|
0 |
|
t |
|
0 |
|
t |
|
||||||
i = C |
C |
= |
|
e |
|
Ц |
= |
|
|
e |
|
Ц |
() |
||
dt |
t Ц |
|
|
r |
|||||||||||
|
|
|
|
|
|
|
|||||||||
с течением времени убывает по экспоненте, направление его совпадает с выбран-
ным при составлении дифференциального уравнения условно положительным -на правлением.
Аналогично изменяется и напряжение на активном сопротивлении:
- |
t |
|
|
|
t Ц |
|
|||
ur = ir = U0 e |
() |
|||
. |
||||

В момент включения источника питания значение иr изменяется скачком от
нуля до максимума. График изменения иr(t) изображен на рисунке 8.2. Здесь же по-
казана кривая uСВ(t).
Во время переходного процесса в емкости происходит непрерывное накоп-
ление электрической энергии, которая при t®µ достигает величины
WСmax = CU02/ 2.
Одновременно часть энергии, отдаваемой источником питания, расходуется в активном сопротивлении. Причем энергия, теряемая в сопротивлении, равна энер-
гии, запасаемой в емкости.
Если напряжение на емкости к моменту включенияравно UН, начальные
условия должны быть записаны в виде:
UС (0+) = UС(0–) = UН .
В этом случае напряжение uС определяется формулой:
- |
t |
æ |
- |
|
t |
ö |
|
- |
t |
|
|
|
|
|
|
|
|
||||||
uC = U0 - ( U0 - U Н )e t Ц |
ç |
t |
÷ |
Н e |
t Ц . |
|
|||||
= U0 ç 1 - e |
|
|
Ц ÷ + U |
() |
|||||||
|
|
ç |
|
|
÷ |
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
Таким образом, в цепи первого порядка свободная составляющая имеет
вид:
iСВ ( t ) = Ае р t ,
т. е. выражается экспоненциальной зависимостью, крутизна которой определяется
р – корнем характеристического уравнения(показателем степени экспоненты).
Постоянную А называют постоянной интегрирования.
Величина i( 0+ ) является зависимым начальным условием и определя-
ется из схемы после коммутации с учетом независимых начальных условий.
Независимым начальным условием является напряжение на ёмкости, причем в схе-
ме до коммутации.
Постоянная времени – время, в течение которого свободная составляющая изменится в е раз.
Длительность переходного процесса в цепях первого порядка обычно не превышает нескольких tЦ:
t ПП » 3 ¸ 5tЦ.
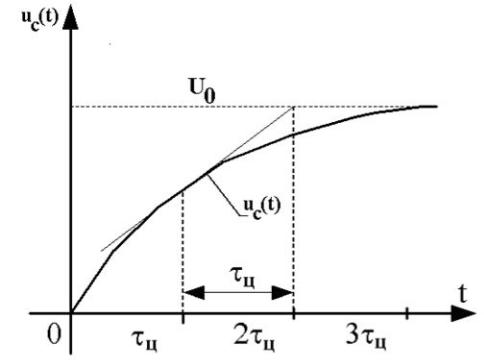
Постоянная времени может быть определена также графическим методом
– по длине под касательной (рисунок 8.3).
Рисунок 8.3 – Графическое определение постоянной времени цепи
При построении графиков целесообразно вести расчет для моментов времениt = 0, tЦ, 2tЦ, 3tЦ и т. д. При этом можно использовать таблицу 8.1.
- |
t |
|
|
t Ц в зависимости от tЦ |
|||
Таблица 8.1 – Значения e |
|||
t |
0 |
tЦ |
2tЦ |
3tЦ |
4tЦ |
5tЦ |

|
- |
|
t |
|
|
|
|
|
|
|
|
|
|
|
1 |
0,368 |
0,135 |
0,050 |
0,018 |
0,007 |
|
e |
t |
Ц |
|
|||||||
|
|
|
|
|||||||
Можно отметить, что величина р (или tЦ) зависит от пассивных элементов схе-
мы (R, L и C) и характеризует длительность переходного процесса в конкретной це-
пи. В цепи первого порядка р всегда отрицательно.
Это означает, что изменяющиеся во время переходного процесса токи и на-
пряжения стремятся к своему устойчивому состоянию, и переходный процесс затухает.
Алгоритм расчета переходного процесса классическим м
в цепи первого порядка следующий.
1 Для схемы до коммутации определяются независимые начальные условия.
2 Для схемы после коммутацииопределяются зависимые начальные усло-
вия.
3 Для схемы после коммутации определяются вынужденные составляющие.
4 Для схемы после коммутациипо методу входного сопротивления опреде-
ляется корень р характеристического уравнения: определяют полное комплекс-
ное сопротивление цепи после коммутации, считая сопротивление индуктивности
xL = jw L , а сопротивление емкости xС = 1 jwС , осуществляют замену jw на p и
приравнивают Z(p) = 0. Входное сопротивление Z(p) может быть определено отно-
сительно любой ветви схемы. При определении Z(p) источники ЭДС в схеме зако-
рачиваются (внутреннее сопротивление идеальной ЭДС равно нулю), а источники тока – размыкаются (внутреннее сопротивление идеального источника тока равно бесконечности).
5 Определяются постоянные интегрирования для тока или для напряже-
ния: А = i( 0+ ) - iВЫНУЖД ( 0 ) ; B = u( 0+ ) - uВЫНУЖД ( 0 ).
6 Записывается окончательный результат в виде:
i( t ) = iВЫНУЖД ( t ) + Ae pt , или u( t ) = uВЫНУЖД ( t ) + Be pt .
