Аналитический
Функция
представлена в виде алгебраического
выражения называется логическая
операция, если вернуться к таблице №3
можно заметить что f(x1,x2,x3)
f=
x3
v
v
x1x2x3
Числовой
Каждый набор считают двоичным числом, причем самую левую и самую правую переменную считают самым старшим и самым младшим разрядом числа. Функцию задают в виде десятичных номеров тех наборов переменных, на которых она принимает значение 1. Для таб. 3 f{1,3,7}x1x2x3 функция принимает значение 1.
N= …k23+k22+k21+k20
k=0.1
Каждое число F различны хотя бы на одно наборе переменных ФАЛ от n переменных можно получить F=2n где n число наборов для n переменных.
F=(22)n (2)
Фал от двух переменных.
Согласно с выражением 2, при n=2 => F=(22)2=16.
Эти функции носят название элементарные.
x1 |
x2 |
f0 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
Название и условное обозначение |
Ни когда f0=0 |
Конъюнкция «И» ^& |
Операция «НЕ» запрет=→ |
Тоже f3= x1 |
Запрет по x1 =← |
Повтор f5= x2 |
Альтернатива + |
Операция «ИЛИ» V + дизъюнкция |
Операция «ИЛИ НЕ» стрелка Пирса↓ |
Равнозначность ≡ |
Операция «НЕ» f10= x2 |
«ЕСЛИ ТО» импликация↑ |
«НЕ» f12= |
«ЕСЛИ ТО» импликация↑ |
«И-НЕ» |
«ВСЕГДА» f15=1 |
||
f0=0, const нуля
f1= x1 x2= x1* x2 операция конъюнкция (логическое умножение)
f2 =→ x1 = x2 = x*
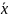2
запрет
по x2
f3 =←x1 повтор по x1
f4= x1 = x2 = 1*x2 запрет по x1
f5=x2 повторение по x2
f6=x1 + x2 = x1* 2 v 1*x2 (не равнозначность, альтернатива сложения по модулю е)
f7=x1 v x2 (дизъюнкция); (логическое сложение «ИЛИ»)
f8=x1 + x2= 1 v 2 = 1* 2 (стрелка Пирса) («ИЛИ-НЕ»)
f9=x1≡x2=x1*x2 v 1 2 (тождество, равнозначность)
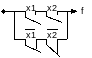
f10= 2
f11=x1←x2=x1 v 2 (импликация)
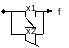
f12= 1
f13=x1→x2= 1 v x2 (Импликация по x1)
f14=x1┴x2= 1* 2= 1 v 2 (штрих Шеффера) («И-НЕ»)
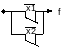
f15=1 → короткое замыкание
Три функции И, ИЛИ, НЕ получили название основных функций, то есть любую функцию алгебры логики можно заменить используя эти три функции