Теория дискретных устройств. Дискретные элементы. Дискретные устройства. Система управления. Основные понятия.

В системах управлениях промежуточной работы с информацией носит информационный сигнал. Под сигналом материальное воплощение сообщения. Управление аппаратуры состоит из элементов, каждый элемент предназначен для конкретного преобразования сигнала. Сигнал является функцией от времени. U(t) и I(t). Сигналы делятся на три группы:

1. Непрерывные;

2. Многозначные;

3. Дискретные (двоичные)

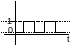
Сигналы, медленно меняющиеся во времени и не прерывные в некотором интервале относительно каналов.

Дискретный сигнал величина у него изменяется скачкообразно переходя с одного уровня на другой. Если сигнал меняется между «0» и «1» - двоичный сигнал.

Дискретный элемент – устройство преобразующий двоичный сигнал.

Дискретная система управления – система, в которой информация обрабатывается в дискретной форме.

Дискретные элементы и их характеристики.

В дискретных системах управления основные операции часто повторяются, к этим операциям относятся логические операции.

Дискретный элемент – минимальная совокупность деталей объединённых в общую схему и выполняющих, какую либо основную функцию и имеющих релейную характеристику, у которой при не прерывном изменении входного сигнала, выходной сигнал меняется скачком.

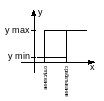
Характеристики дискретных элементов.

1. Амплитудные (U, I, W_вкл. для микросхем W_{переключения} из «0» в «1» U_min=0; U_max=1; U, I, W_выкл. из «1» в «0»).

2. Временные t_вкл из «0» в «1» t_выкл из «1» в «0»

3. Нагрузочная

- коэффициент объединения по входу (показывает, сколько входов микросхемы можно объединить).

- коэффициент разветвления по выходу (сколько входов можно подключить к одному выходу предшествующего логического элемента).

Примеры дискретных элементов.

Реле является дискретным элементом, существуют реле I и не I класса надежности.

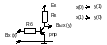
Такая схема называется инвертор от «0» к «1» или «1» в «0».

Диодный резистор логического элемента

Схема «ИЛИ» для положительных сигналов.

1. y=x₁

2. y=x₂

3. схема выделяет максимальное значение сигнала.

УГО:

,

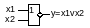где v-ИЛИ

Схема «И» для положительных сигналов.

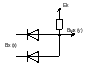
y=x₁x_x

1. вых 0

2. вых 1

Под 1 напряжение близкое или больше Ек.

Схема «И» для отрицательных сигналов.

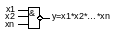
Схема «И+НЕ»

Схема «И-НЕ»

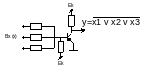
«И»

«ИЛИ»

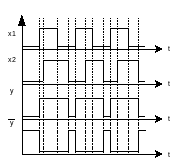
Анализ и синтез комбинационных автоматов.

Все дискретные автоматы:

- комбинационные

- автоматы с памятью

Комбинационный автомат – автомат состояние выхода определяется только по состоянию его входа, и отсутствием внутреннего состояния автомата. Для его задания надо знать x,y,z; z(t)=ψ (x(t),y(t)).

Автомат, в котором функция выхода z определяется не только состоянием входа ну и внутреннем состояние автомата будет автомат с памятью или конечный автомат.

Основные определения и задание функций алгебры логики.

При анализе и синтезе дискретных автоматов наибольшее практическое распространение получили двоичные количественные величины, элементы и системы. Математический алгоритмом, описывающим их является алгебра логики или Булева алгебра, предложенная Джоном Булем. Логической переменной называется величина, которая может принимать одно из двух значений. Булево функцией или ФАЛ (функция алгебры логики) f(x₁ x₂…x_n) где x₁ x₂…x_n логические переменные - называется функция, которая так же может принимать одну из двух значений. Два значение, которые принимают логические переменные и ФАЛ приниматься обозначать «0» и «1». Эти цифры являются символические и не выражают количественного значение величины, таким образом, Булева алгебра – это алгебра символов, а не алгебра чисел. Наборам для ФАЛ называется комбинация (сочетание значений) всех логических переменных являющиеся аргументами этой ФАЛ. Так как переменные ФАЛ могут только два значения, то область определения любой ФАЛ конечна. Число N наборов для ФАЛ от n – переменных конечно N=2ⁿ. Для n=2 существует четыре следующих набора ФАЛ:

00, 01, 10, 11

Для n=3

000, 001, 010, 011, 100, 101, 110, 111.

Существует несколько способов задание ФАЛ.