13.3. Типовые задачи инвестиционного анализа

Обычно рассматривают два вида инвестиций: реальные и финансовые. Реальные инвестиции — инвестиции в какой-либо тип материально осязаемых активов, таких, как земля, оборудование, организации. Финансовые инвестиции представляют собой вложения в акции, облигации и другие ценные бумаги, выпущенные частными организациями и государством, а также в банковские депозиты. Оба вида инвестиций между собой тесно связаны. С обновлением и расширением основных фондов непосредственно связаны реальные инвестиции. Источником финансирования реальных инвестиций могут быть доходы, полученные от финансовых инвестиций. Реальные инвестиции — это долгосрочные инвестиции, с получением дохода через определенное время (несколько месяцев или лет) и в течение продолжительного времени, причем поступления доходов от инвестиций зависят от колебаний конъюнктуры рынка.

При анализе доходности инвестиций требуется экономическое обоснование и прогнозирование будущих условий, поэтому инвестиционный анализ в значительной степени прогнозный, и в применяемых методиках учитывается фактор времени и степень риска.

1. Учет фактора времени. При оценке эффективности инвестиций должны учитываться такие аспекты фактора времени, как динамичность (изменение во времени) параметров проекта и его экономического окружения — концепция жизненного цикла системы, разрывы во времени (лаги) между производством продукции или поступление ресурсов и их оплатой, неравноценность средств, относящихся к различным моментам времени. Неравноценность объясняется тем, что имеющиеся в настоящий момент денежные средства могут быть инвестированы и принести доход в будущем. Поэтому денежные средства, не инвестированные сегодня, не принесут дохода в будущем и со временем обесценятся.

2. Учет степени риска выражается в том, что эффективность инвестиционного проекта оценивается с определенной вероятностью.

Все задачи, которые возникают в процессе инвестиционного анализа, можно свести к шести типам, решаемым с помощью несложных математических функций. Каждая из функций строится на знании следующих исходных данных:

• нормы дисконта;

• периода начисления;

• дохода от инвестиций.

Норма дисконта — это основной задаваемый экономический норматив, используемый при дисконтировании денежных потоков. Дисконтированием денежных потоков называется приведение их разновременных (относящихся к разным шагам расчета) значений к ценности на определенный момент времени, который называется моментом приведения.

Для собственников капитала норма дисконта идентифицируется с нормой дохода (процентной ставкой), ожидаемой от вложений капитала, поэтому чем больше шансы потерь, тем выше ставка дисконтирования, по которой разновременные доходы на инвестиции приводятся к моменту инвестирования.

Дисконтирование широко используется в практике зарубежных стран, где норму дисконта (норматив приведения по фактору времени) связывают с риском деловых операций (табл. 13.3).

Таблица 13.3. Связь ставок дисконтирования с риском деловых операций

Степень риска	Направление инвестирования	Норма дисконта, %
Очень низкая	Рефинансирование выпуска облигаций	7
Средняя	Обычные проекты	16
Высокая	Новые проекты на стабильном рынке	20
Очень высокая	Новая технология	24

Приведение по фактору времени (дисконтирование) используется только в расчетах оценки эффективности вариантов инвестирования. Этот принцип не учитывается при определении плановых и фактических показателей эффективности систем (прироста прибыли, снижения себестоимости и т.п.).

Сумма дисконта зависит:

• от разрыва во времени между оттоком и притоком денежных средств;

• от необходимой ставки процента или дисконта;

• от риска вложений.

Периодом начисления служит временной интервал, к которому приурочена норма дисконта. В аналитических расчетах в качестве периода начисления применяется, как правило, период, кратный году.

Доход от инвестиций определяется в процессе прогнозных аналитических расчетов. При определении ставки дохода на инвестиции как основного финансового критерия используется эффект сложного процента.

Рассмотрим основные инвестиционные задачи (табл. 13.4).

Таблица 13.4. Типовые задачи, решаемые в инвестиционном анализе

Инвестиционные задачи	Функции
Расчет дохода на инвестиции через определенное число лет	Множитель наращения (накопленная сумма единицы (F1) ,
Расчет накоплений, депонированных в конце каждого периода	Фактор накопления единицы за период (F2)
Расчет приведенной (текущей) стоимости дохода, полученного от инвестиций	Текущая стоимость единицы (реверсия) (F3)
Расчет текущей стоимости денежного потока, получаемого ежегодно (ежеквартально)	Текущая стоимость аннуитета (F4)
Расчет необходимого ежегодного (ежеквартального) дохода для возмещения инвестиций	Погашение кредита (F5)
Расчет необходимой суммы, депонированной в конце года для получения определенного дохода	Фактор фонда возмещения (F6)

Задача 1. Определить доход на инвестиции через определенное число лет (кварталов) при заданной процентной ставке и сумму оценки инвестиций через определенный период.

Решение. Применим математическую модель «накопленная сумма единицы», или «множитель наращения (F₁)».

Для определения прироста суммы используем формулу расчета сложного процента:

F₁ = (1 + r)ⁿ,

где  r   — ставка дисконта;

F₁ — множитель наращения (коэффициент приведения);

n   — период наращения;

m – число платежей в течение года.

Накопленная за период сумма (S_n) определяется как произведение начальной суммы инвестиций и функции наращения:

S_n = S₀(1 + r)ⁿ, или S_n = S₀  F₁, (13.2)

где S₀ — сумма инвестиций в начальный момент времени.

При использовании данной функции исходят из предположения, что ежегодный доход от инвестиций реинвестируется или капитализируется.

Пример. В покупку объекта недвижимости, например земли, вложено 100 тыс. руб. Ставка доходности — 10% годовых. Чему будет равна цена земли через 5 лет?

S_n = 100 (1 + 0,1)⁵ = 161,05 тыс. руб.

Доход от вложений равен 61,05 тыс. руб. 

Задача 2. Определить стоимость серии равных сумм вложений, депонированных в конце каждого из периодических интервалов.

Решение. Применим фактор накопления единицы за период:

(13.3)

где — фактор накопления единицы за период n.

Формула (13.3) представляет собой сумму членов геометрической прогрессии со знаменателем (1 + r), которая имеет следующий вид:

(13.4)

Накопления, полученные при депонировании вкладов в начале каждого периода, могут быть рассчитаны путем суммирования сложных процентов за весь рассматриваемый период.

Эта модель чаще применяется при определении доходности банковских операций с вкладами, но может использоваться и при оценке доходности реальных инвестиций.

Накопленная стоимость за период составит:

S_n = a  F₂, (13.5)

где а — аннуитет — денежный поток с равными поступлениями.

Задача 3. Определить текущую стоимость средств от инвестиций в будущем.

Решение. Для решения применим факторный множитель «текущая стоимость единицы (реверсии)» — это величина, обратная накопленной сумме единицы. Решение этой задачи позволяет привести суммы, планируемые к получению в будущем, к настоящему времени.

Фактор текущей стоимости (реверсии) рассчитывается по формуле

(13.6)

где F₃ — реверсия (коэффициент приведения к начальному моменту времени).

Текущая стоимость рассчитывается как произведение стоимости, прогнозируемой к получению в будущем, и фактора F₃:

PV = S_n  F₃, (13.7)

где PV — текущая стоимость будущих средств.

Пример. При ставке дисконта, равной 10%, текущая стоимость 100 тыс. руб., ожидаемая к получению через год (100 тыс. руб., полученные через год, с точки зрения ценности сегодняшнего периода), составит:

 

Задача 4. Привести стоимость суммы средств, подлежащих к получению в течение ряда периодов (лет), к их стоимости на сегодняшний день.

Решение. Алгоритм решения этой задачи идентичен определению текущей, дисконтированной стоимости денежного потока, генерируемого в течение ряда равных периодов времени в процессе реализации какого-либо проекта.

Отдельные элементы денежного потока относятся к разным временным интервалам, поэтому их суммирование искажает реальную доходность инвестиций.

Приведение стоимости денежного потока к одному моменту времени осуществляется с помощью функции, называемой текущей стоимостью аннуитета:

, (13.8)

где n — число периодов получения дохода от инвестиций.

Текущая стоимость аннуитетов определяется по формуле

PV = a  F₄. (13.9)

Формула (13.9) применяется для определения текущей стоимости, если доходы, получаемые за каждый i-й период, равны.

При неравенстве доходов по временным периодам их получения проводится расчет дисконтированной стоимости за каждый период.

Пример. В результате осуществления инвестиционного проекта ежегодные доходы в течение 5 лет будут составлять по 100 тыс. руб.

Текущая стоимость денежных потоков составит:

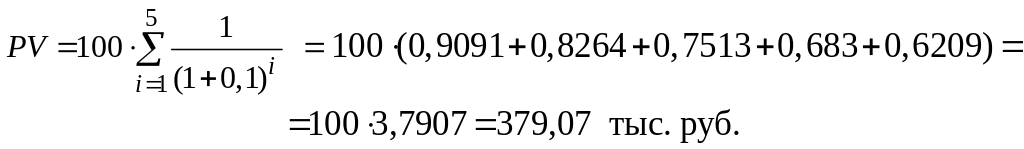
В результате дисконтирования дохода за каждый период получим за 5 лет по стоимости на сегодняшний день:

(90,91 + 82,64 + 75,13 + 68,30 + 62,09) = 379,07 тыс. руб. 

Задачи 3 и 4 наиболее часто применяются в анализе инвестиционных проектов.

Задача 5 (обратная задаче 4). Определить сумму, подлежащую получению, чтобы возместить (окупить) инвестиции за определенный период времени с учетом процентной ставки. Задачу можно поставить так: какую сумму необходимо ежегодно (ежеквартально) вносить в банк для погашения кредита и процентов по нему?

Решение. Содержание задачи определяет название функции, применяемой для ее решения, — функция погашения кредита, которая определяется как величина, обратная текущей стоимости аннуитета:

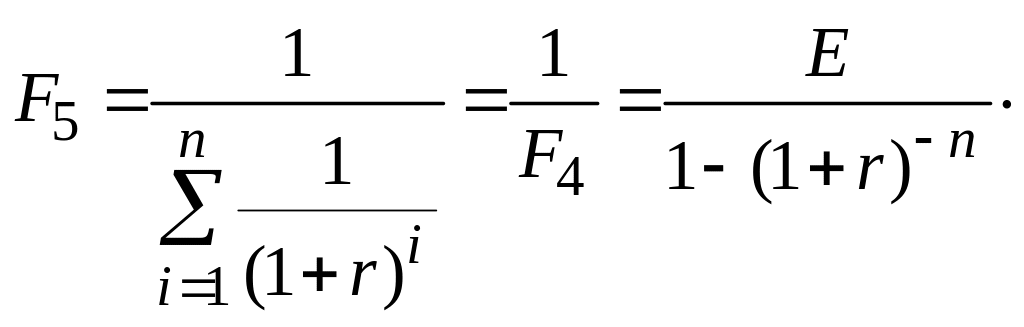(13.10)

Ежегодный доход (аннуитет) определяется умножением суммы инвестиций на множитель F₅:

FV = S₀  F₅. (13.11)

Пример. Инвестиции в проект составили 500 тыс. руб. Чтобы окупить инвестиции в течение 5 лет и получить доход в размере 10% годовых, ежегодный денежный поток (аннуитет) должен составить:



Задача 6. Определить сумму, подлежащую ежегодному вложению на депозитный счет в банк, чтобы через определенное число лет получить заданную сумму средств.

Решение. Для решения используем функцию «фактор фонда возмещения» — величину, обратную фактору накопления единицы за период:

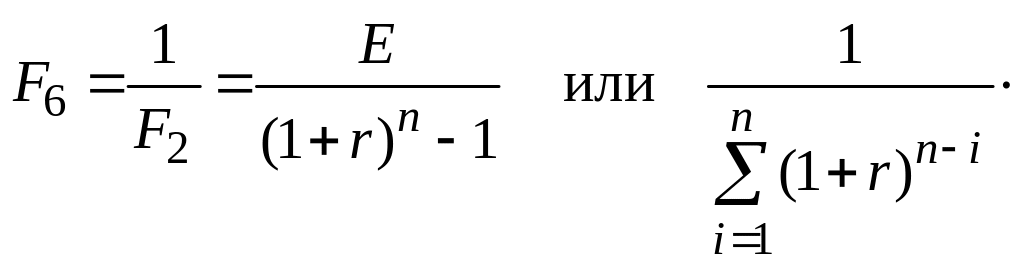(13.12)

Сумма ежегодного вклада составит:

FV = A  F₆, (13.13)

где А — стоимость поступлений по истечении срока вложений.

Фактор фонда возмещения показывает денежную сумму, которую необходимо депонировать в конце каждого периода, чтобы через заданное число периодов остаток составил необходимую сумму (например, 100 тыс. руб.). Этот фактор учитывает процент, получаемый по депозитам.

Пример. Чтобы получить 500 тыс. руб. в конце четырехлетнего периода при нулевом проценте, необходимо депонировать Если процентная ставка составит 10%, тогда (по предыдущему примеру) можно депонировать 88,89 тыс. руб. в конце каждого года. Разница четырех взносов и полученной суммы составит 144,44 тыс. руб. 

Часто в тех случаях, когда вплоть до истечения срока кредитного договора (долгового обязательства) кредитору выплачивается только процент, заемщики для погашения основной суммы кредита создают специальные фонды возмещения. В каждый период должник вносит в отдельный фонд сумму, которая вместе с начисляемым на нее процентом должна обеспечить погашение основной части кредита.

К одной из рассмотренных выше задач или их сочетанию может быть сведена любая инвестиционная задача.