2.2. Назначение основных размеров плиты

Расчетный пролет:

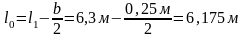
Высота плиты:

Где q_п – нормативная продолжительная нагрузка (постоянная и длительная) в кН/м² ; Vп – нормативная кратковременная нагрузка в кН/м2.

Принимаем h_n = 0,27 м.

Основные размеры поперечного сечения плиты. (Размеры плиты назначены по рекомендациям прил. 3 и рис. 5).

Рис. 2.1 - Поперечное сечение плиты

Расчет по 1-ой группе предельных состояний

2.3.1. Расчет полки плиты на изгиб

Для расчета выделяют полосу плиты шириной в один метр. Сбор нагрузок на полку (кН/м) (табл. 2.1.).

Таблица 2.1. - Загружение полки плиты

Наименование нагрузок	qn, кН/м	γ f	q, кН/м
1. Вес пола (см. табл. 1.1)	1,2	–	1,46
2. Вес полки 0,03х25	0,75	1,1	0,825
3. Временная нагрузка	4,7	1,2	5,64
Итого х γ n	6,65	–	7,925

Изгибающий момент (рис. 2.2):

Рис.2.2 - Схема работы полки плиты

Полезная высота сечения при расположении арматуры в середине полки:

Подбор сечения арматуры:

Расчёт сварной сетки: : Принимаем минимальную сварную сетку по ГОСТ 8478-8 с площадью А =0,35см⁴ 5О5Вр-1

2.3.2. Предварительный подбор сечения продольной арматуры

Изгибающий момент в середине пролета:

В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки приведенного таврового сечения (рис.2.3) принимается равной фактическому значению (h_f’ = 3 см). Ширина полки b_f’, вводимой в расчет, принимается равной всей ширине верхней полки плиты, так как имеет место:

                                                                         [2, п.3.16].

Ширина ребра:

Предположим, что нейтральная ось проходит в пределах полки (I случай), то есть

 [1, п. 3.3].

где ho = h – a = 27 – 3 = 24

;

0,03м, следовательно, нейтральная ось проходит в пределах полки (подтверждается первый случай расчета).

Рис.2.3 – Сжатая полка сечения плиты

Для вычисления коэффициента условия работы   по формуле:

                                        [2, формула (27)]

принимаем предварительно  . Для арматуры A-V коэффициент   [2, п.3.13].

Тогда

Принимаем   Требуемое сечение арматуры равно:

=4,522*10^-4

Принимаем 10 диаметров 8 (A_sp=5,03см²) (прил. 4). Размещение арматуры приведено на рис. 2.4.

Рис.2.4 – Размещение арматуры.

2.3.3. Определение приведенных характеристик сечения

Заменяем пустоты равновеликими по площади и моментам инерции прямоугольниками.

Круглые пустоты приводят к квадратному сечению со стороной 

h_red = 0,9*19=17,1 см

Толщина полок, приведенного сечения:  h_f=h^’_f=(27-17,1)*0,5=4,95

Ширина ребра b = 216-8*17,1=79,2 см. (рис.2.7).

                                                                     [2, п.4.5]

Рис.2.5 –Приведенное сечение плиты

Приведенная площадь сечения:

Приведенный статический момент относительно нижней грани сечения:

Положение центра тяжести приведенного сечения:

Приведенный момент инерции:

.

Момент сопротивления по нижней зоне:

то же по верхней зоне: