2. Определение напряжений в грунтовом массиве

Напряжения в грунтовом массиве возникают как от действия внешних сил, так и внутренних - собственного веса грунта. Величины образовавшихся в грунтовом массиве напряжений оказывают влияние на развитие деформаций, обусловливающих осадки и деформации сооружений, устойчивость грунтовых откосов, давление грунта на подпорные стенки.

Для решения задачи распределения напряжений в грунтовом массиве в механике грунтов применяют теорию линейно- деформируемых тел, для которых справедливы положения теории уп­ругости, базирующиеся на линейной зависимости между напряжения­ми и деформациями в упругой стадии (закон Гука). Однако для дис­персных грунтов закон Гука в общем случае будет неприемлем, так как при давлениях, превышающих структурную прочность грунтов, возникают не только упругие, но и пластические (остаточные) дефор­мации.

Применяя к грунтам зависимости теории упругости, следует иметь в виду, что они предусматривают постоянство или закономерность изменения свойств грунтов с глубиной. Но грунтовые напластования, образовавшиеся в результате длительных геологических процессов, неоднородны. Кроме того, в грунтовом массиве формируются напря­жения от собственного веса грунта. В результате взаимодействия его с напряжениями, вызванными внешними нагрузками, в массиве созда­ется сложное напряженное состояние, описываемое тензором второго ранга, называемым тензором напряжений .

Тензор напряжений записывают в виде матрицы его компонентов:

, (33)

где — нормальные, 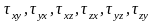— касательные напряжения.

Тензоры напряжений являются симметричными, т.е = , 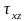= , = . Поэтому в общем случае тензор напряжений может быть полностью охарактеризован шестью его компонентами. Иначе говоря, чтобы вычислить значения напряжений на площадках, любым произвольным образом ориентированных в пространстве, дос­таточно знать составляющие нормальные и касательные напряжения, действующие на трех любых взаимно перпендикулярных площадках.

Каким бы ни было поле напряжений грунтового массива в целом и напряженное состояние в любой точке рассматриваемого массива, в каждой из точек существуют три такие взаимно ортогональные на­правления (притом единственные), при которых все касательные ком­поненты тензора напряжений равны нулю. Отличными от нуля оста­ются только три нормальных напряжения

и , называемые главными нормальными напряжениями. Матрица тензора напряжений, выраженная главными его значениями, примет вид

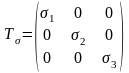(33')

Индексы 1, 2 и 3 в матрице тензора обычно присваивают главным напряжениям таким образом, чтобы было алгебраически макси­мальным, промежуточным значением, - алгебраически мини­мальным.

1. Определение напряжений от действия сосредоточенной силы

От действия силы N, приложенной в т. О перпендикулярно к горизонтальной плоско­сти, ограничивающей линейно деформируе­мое полупространство (рис.11), во всех точ­ках полупространства, удаленных от т. О, возникает сложное напряженное состояние, характеризующееся напряжениями и перемещениями S_x, S_y, S_z.

Рис. 11. Схема к оп­ределению напряжений

от действия сосредото­ченной силы

В строительной практике наибольший ин­терес представляет закономерность распре­деления нормальных вертикальных напряже­ний σ_Z.

В грунтовом массиве возьмем т. М, по­ложение которой определяется полярными координатами R и β, в системе координат с началом в точке О приложения силы N.

Для упрощения вывода примем как по­стулат, что напряжение σ_R пропорционально Сosβ и обратно пропор­ционально квадрату расстояния R² от точки приложения сосредото­ченной силы до т. М:

(34)

где А - коэффициент пропорциональности, определяемый из условия равновесия:

(35)

Подставив значение А из формулы (35) в формулу (34), получим

(36)

Отнесем величину радиальных напряжений не к площадке, пер­пендикулярной к радиусу, а к площадке, параллельной ограничиваю­щей плоскости и составляющей с ней угол . Получим

(37)

Положение точки М определяется двумя координатами z и r, тогда

(38)

где z - глубина рассматриваемой точки от ограничивающей полупро­странство плоскости;

r - расстояние по горизонтали от т. М до оси Z, проходящей через точку О приложения сосредоточенной силы (рис. 11).

Подставив значение R из формулы (38) в формулу (37), получим

Введя обозначение

Окончательно получим

(39)

где коэффициент К табулирован в зависимости от соотношения r/z (табл. 6).