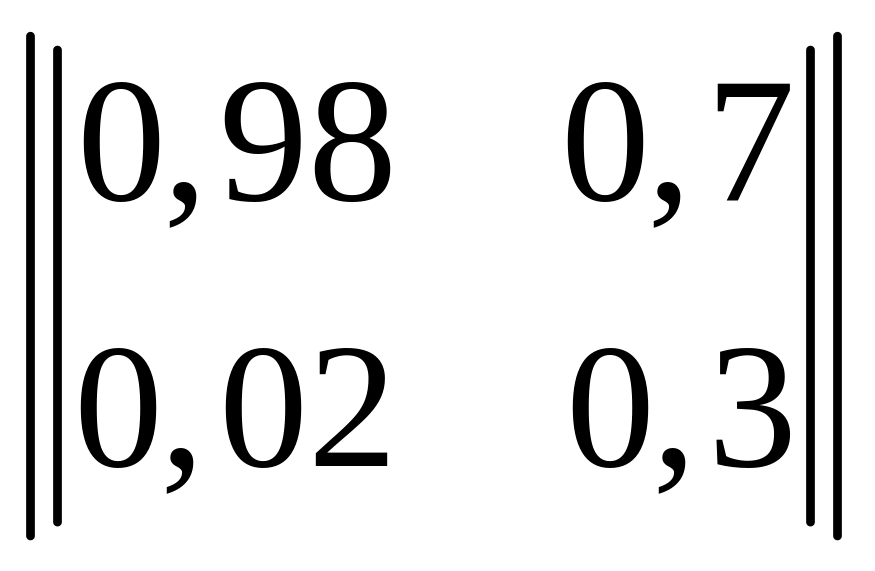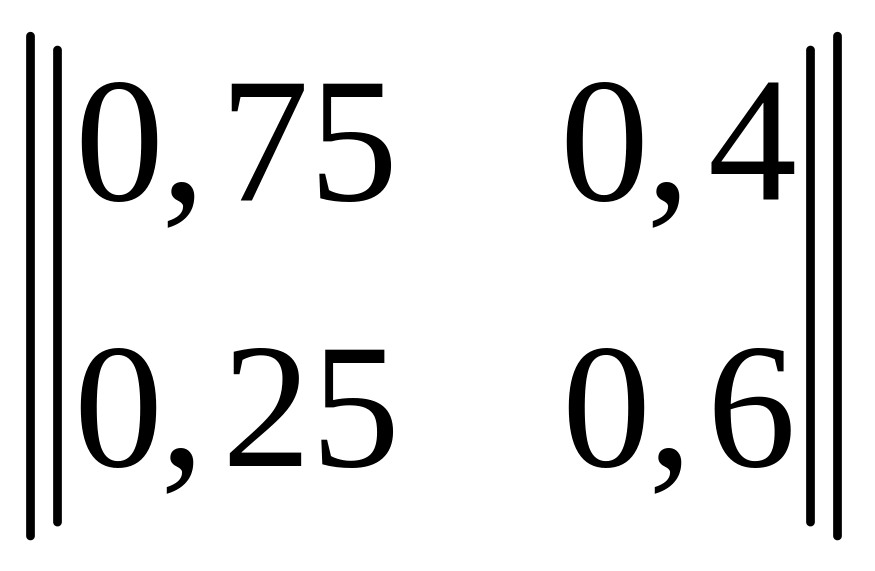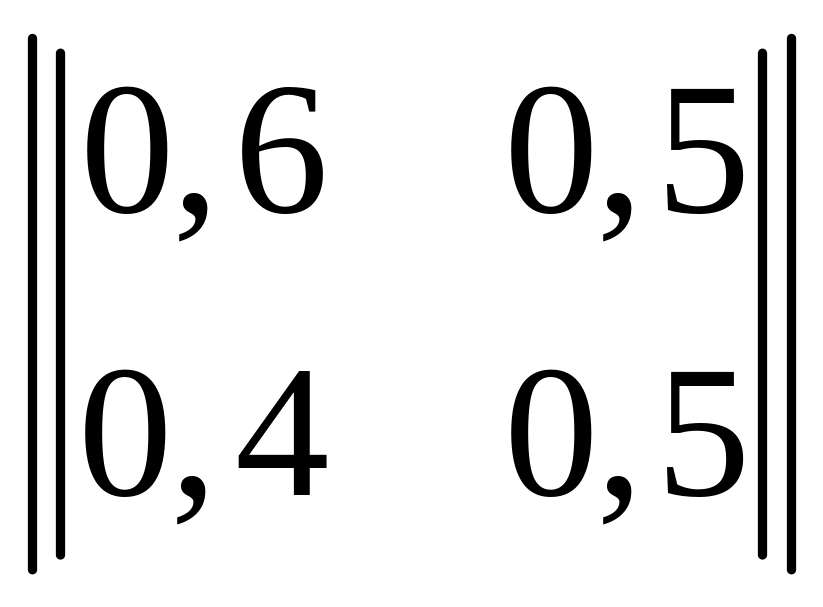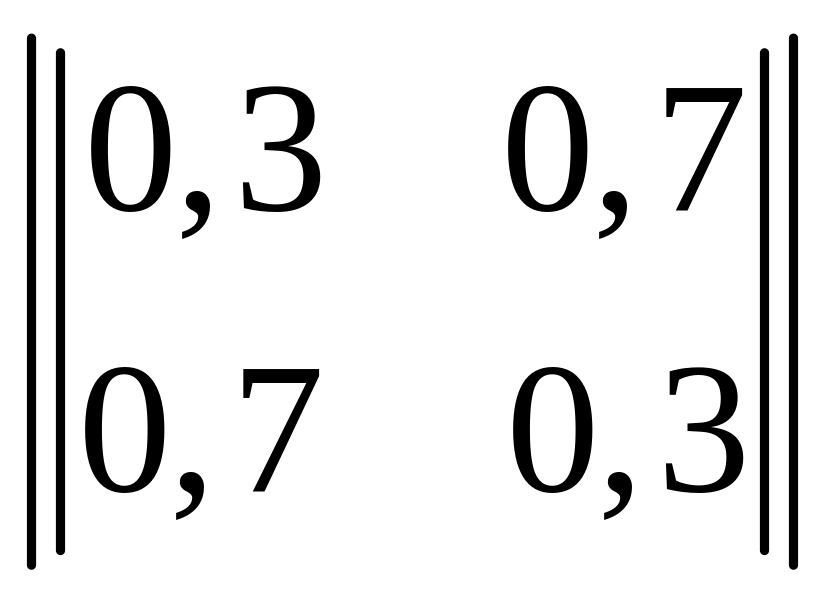1. Информационные характеристики источника сообщений и канала связи
1.1. Основные информационные характеристики
Пусть
- ансамбль сообщений,
- вероятность
-го
сообщения.
Количество
собственной информации
в сообщении
определяется выражением
|
(1.1) |
.
Условная
информация сообщения
при известном
:
|
(1.2) |
.Взаимная информация двух сообщений и :
|
(1.3) |
,где
.
Безусловная энтропия сообщения:
|
(1.4) |
.
Условная
энтропия
сообщения ансамбля
относительно
:
|
(1.5) |
.Совместная энтропия двух ансамблей и :
|
(1.6) |
.Избыточность источника без памяти:
|
(1.7) |
.Избыточность источника с памятью:
|
(1.8) |
.Производительность дискретного источника сообщений:
|
(1.9) |
,где
- время передачи одного символа.
Скорость передачи информации по дискретному каналу (информационная скорость) для неравновероятных взаимно независимых символов, имеющих одинаковую длительность:
|
(1.10) |
,где
-
скорость передачи символов (техническая
скорость).
Скорость передачи информации для равновероятных взаимно независимых символов, имеющих одинаковую длительность:
|
(1.11) |
.Скорость передачи информации для взаимно независимых символов, имеющих разную длительность:
|
(1.12) |
.Скорость передачи информации для взаимно зависимых символов, имеющих разную длительность:
|
(1.13) |
.
Пропускная
способность канала связи
,
бит/симв:
|
(1.14) |
.
Пропускная
способность канала связи
,
бит/сек:
|
(1.15) |
.Пропускная способность как зависимость от физических характеристик канала связи:
|
(1.16) |
,где 
- полоса частот и время передачи по
каналу связи;
-
энергия сигнала;
-
плотность мощности шума.
1.2. Задачи к разделу 1
Источник сообщений выдает символы из ансамбля
.
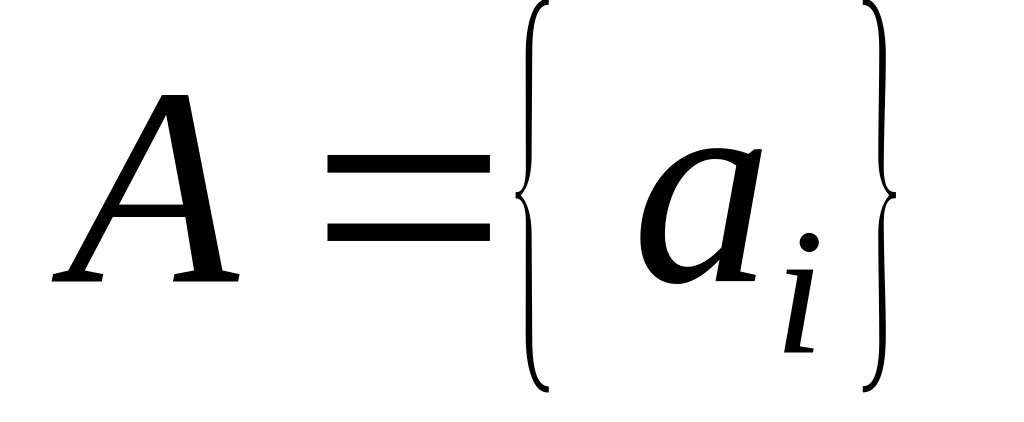Распределения вероятностей приведены
в табл. 1.1. Найти количество информации,
содержащееся в каждом из символов
источника при их независимом выборе
(источник без памяти). Вычислить энтропию
и избыточность заданного источника.
Таблица 1.1
Вариант |
а) |
б) |
в) |
г) |
д) |
е) |
ж) |
з) |
и) |
к) |
|
0,1 |
0,1 |
0,03 |
0,4 |
0,5 |
0,06 |
0,4 |
0,24 |
0,24 |
0,1 |
|
0,25 |
0,05 |
0,26 |
0,25 |
0,04 |
0,15 |
0,18 |
0,18 |
0,28 |
0,1 |
|
0,15 |
0,04 |
0,09 |
0,05 |
0,03 |
0,15 |
0,1 |
0,38 |
0,05 |
0,1 |
|
0,15 |
0,01 |
0,05 |
0,3 |
0,15 |
0,07 |
0,1 |
0,1 |
0,22 |
0,2 |
|
0,3 |
0,2 |
0,16 |
- |
0,04 |
0,05 |
0,06 |
0,06 |
0,15 |
0,35 |
|
0,05 |
0,03 |
0,1 |
- |
0,12 |
0,29 |
0,07 |
0,02 |
0,06 |
0,15 |
|
- |
0,07 |
0,09 |
- |
0,1 |
0,19 |
0,05 |
0,02 |
- |
- |
|
- |
0,5 |
0,22 |
- |
0,02 |
0,04 |
0,04 |
- |
- |
- |
Дискретная последовательность символов, выдаваемых источником, описывается простой цепью Маркова с матрицей переходных вероятностей:
.
Определить энтропию и избыточность двоичного источника без памяти и с памятью, если дискретный стационарный источник задан с помощью матриц переходных вероятностей (табл.1.2).
Таблица 1.2
Вариант |
а) |
б) |
в) |
г) |
д) |
|
|
|
|
|
|
Имеется выборка 100 000 пар совместных событий от дискретных источников
и
.
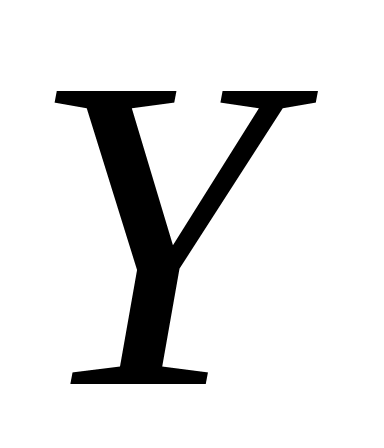Алфавит каждого из дискретных источников
содержит четыре события. Оценки пар
событий получены подсчетами их
относительной частоты и сведены в
табл. 1.3. Определить: энтропии источников
и
;
совместную энтропию источников;
условные вероятности
;
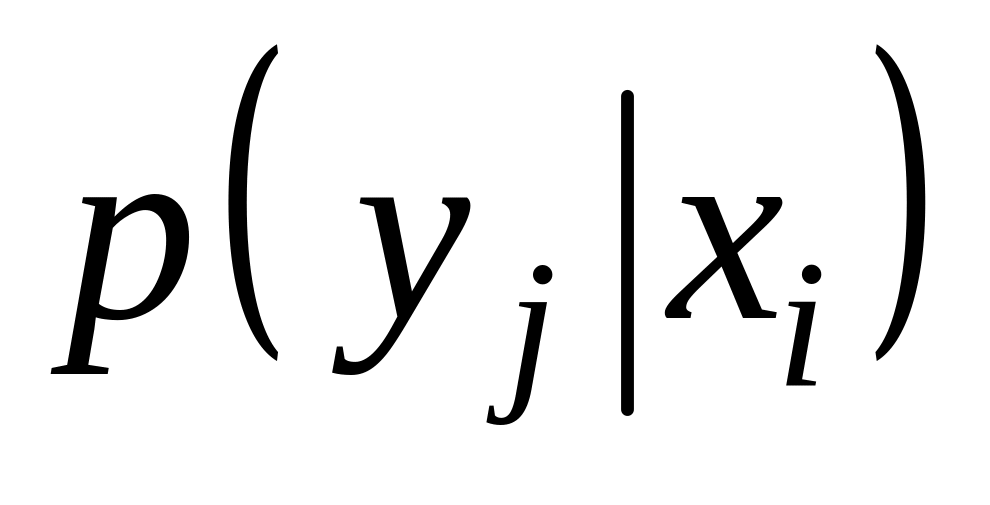условную энтропию
,
.
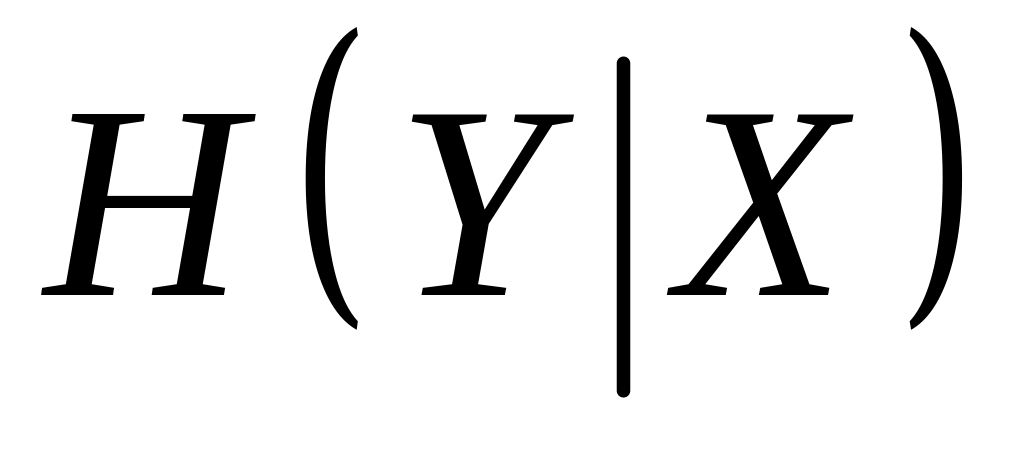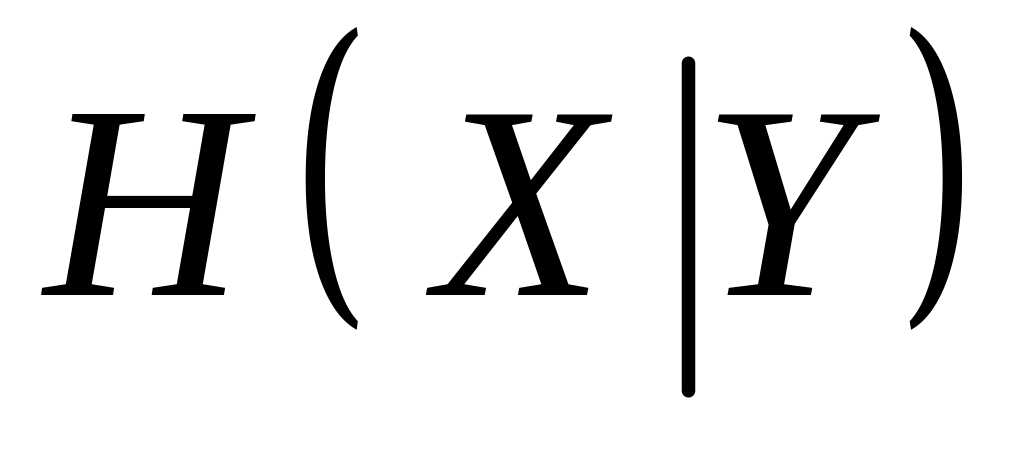Таблица 1.3
В-нт |
|
|
|
|
|
а) |
|
0,10 |
0,05 |
0,05 |
0 |
|
0,05 |
0,15 |
0,15 |
0 |
|
|
0 |
0,10 |
0,10 |
0,10 |
|
|
0 |
0,05 |
0,05 |
0,05 |
|
|
|||||
б) |
|
|
|
|
|
|
0,15 |
0,05 |
0,05 |
0 |
|
|
0,05 |
0,15 |
0,1 |
0 |
|
|
0 |
0,05 |
0,1 |
0,1 |
|
|
0 |
0,1 |
0,05 |
0,05 |
|
|
|||||
в) |
|
|
|
|
|
|
0,15 |
0,05 |
0,05 |
0 |
|
|
0,05 |
0,1 |
0,1 |
0 |
|
|
0 |
0,05 |
0,1 |
0,1 |
|
|
0 |
0,05 |
0,05 |
0,15 |
|
|
|||||
г) |
|
|
|
|
|
|
0,1 |
0,05 |
0,05 |
0 |
|
|
0,05 |
0,1 |
0,1 |
0 |
|
|
0 |
0,1 |
0,2 |
0,1 |
|
|
0 |
0,05 |
0,05 |
0,05 |
|
|
|||||
д) |
|
|
|
|
|
|
0,1 |
0,05 |
0,05 |
0 |
|
|
0,05 |
0 |
0,1 |
0 |
|
|
0,1 |
0 |
0,2 |
0,1 |
|
|
0,1 |
0,05 |
0,05 |
0,05 |
|
Алфавит, из которого строятся передаваемые сообщения, содержит четыре символа
.
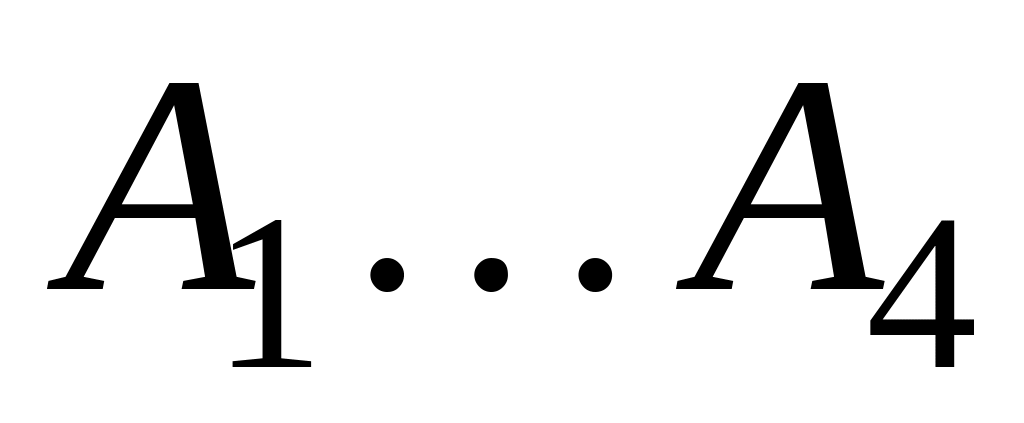Время передачи каждого из символов
соответственно равно:
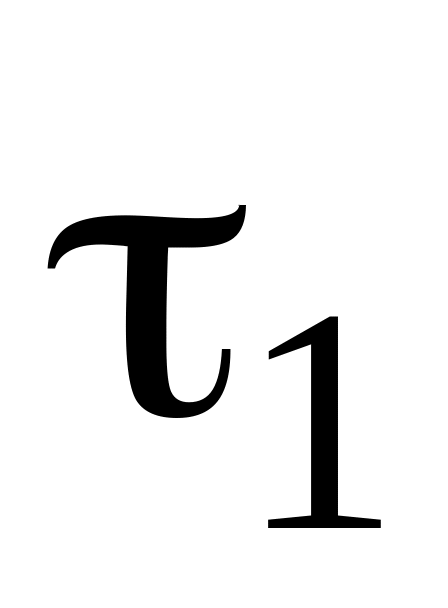=1
мсек;
=2
мсек;
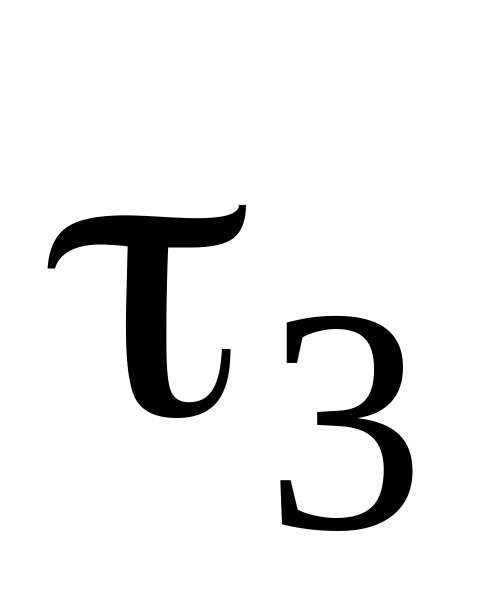=3
мсек;
=5
мсек. Определить скорость передачи
информации:
а) для случая равновероятных символов;
б)
для передачи сообщений со следующими
вероятностями появления символов:
=1/8;
=1/8;
=1/4;
=1/2.
Сообщения составлены из алфавитов А и В. Вероятность появления символов алфавита
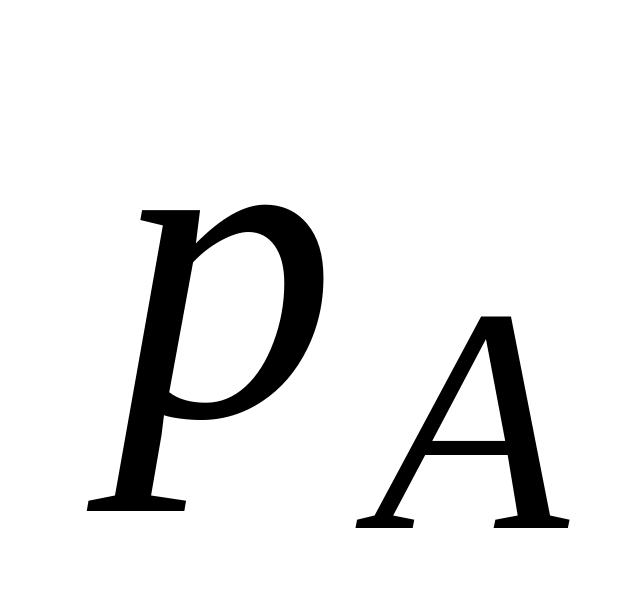=0,6;
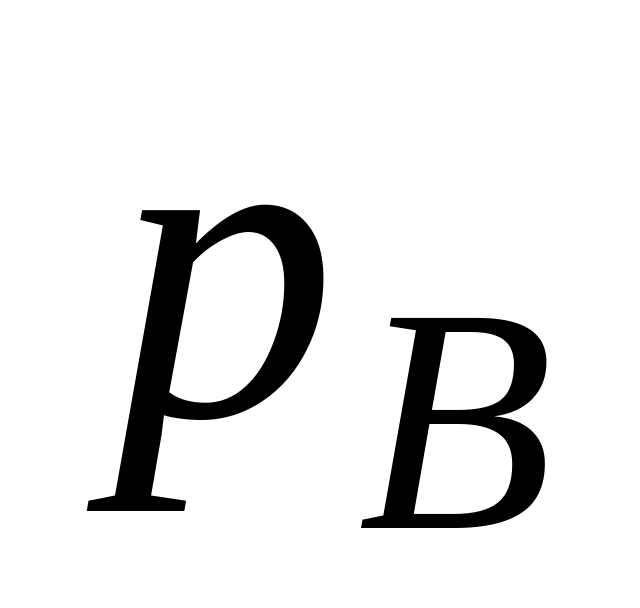=0,4.
Помехи в канале связи заданы канальной
матрицей:
.
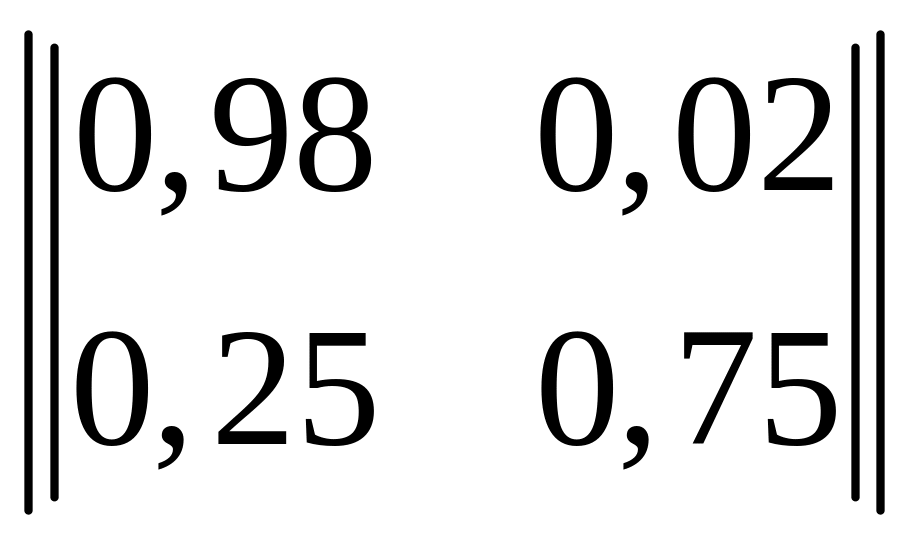Определить скорость передачи информации,
если время передачи одного символа
=2
мсек.Сообщения, составленные из букв русского алфавита, передаются в коде МТК-2 при помощи стартстопного телеграфного аппарата. В начале передачи идёт стартовая посылка, а в конце – стоповая. Буква передаётся пятью элементарными посылками длительностью 1 = 20 мсек. Длина стартовой посылки 2 = 20 мсек, стоповой - 3 = 30 мсек. Определить:
а) скорость передачи информации;
б) скорость передачи информационных символов;
в) время передачи сообщения, состоящего из 450 букв.
Сообщения передаются в двоичном коде. Время передачи «0» 0 = 1 мсек, длительность импульса, соответствующего «1», 1 = 5 мсек. Определить скорость передачи информации для случаев:
а) когда символы равновероятны и независимы;
б) вероятность появления символа «0» р0 = 0,37, вероятность появления символа «1» р1 = 0,63;
в) р0 = 0,2, р1 = 0,8;
г) р0 = 0,02, р1 = 0,98.
Число символов алфавита m = 4. Вероятности появления символов равны соответственно р1 = 0,15, р2 = 0,4, р3 = 0,25, р4 = 0,2. Длительность символов 1 = 3 мсек, 2 = 2 мсек, 3 = 5 мсек, 4 = 6 мсек. Определить скорость передачи сообщений, составленных из данных символов.
Сообщения составлены из пяти качественных признаков (
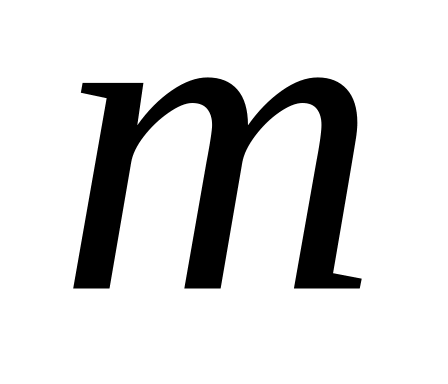=5).
Длительность элементарной посылки
=20
мсек. Определить, чему равна скорость
передачи сигналов и информации.По двоичному каналу связи передается информация со скоростью 14 400 бит/сек. Сколько времени понадобится для передачи 1000 страниц русского текста (энтропия
=
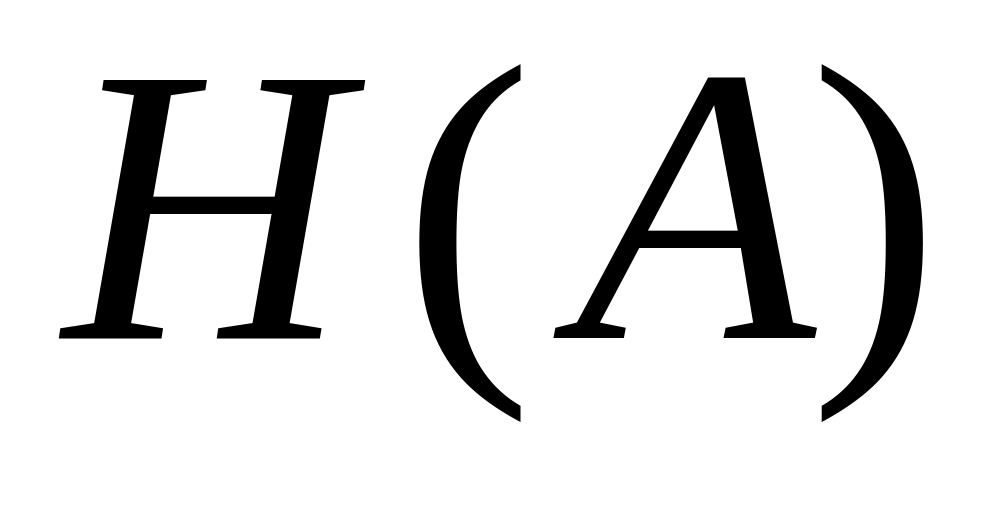5 бит/букву)
с использованием двоичного кода без
избыточности (одна страница - 800 букв
)?По каналу связи без шума могут передаваться четыре сигнала длительностью 1 мсек каждый. Определить емкость такого канала.
Определить пропускную способность дискретного бинарного канала, способного передавать 100 символов «0» или «1» в единицу времени, в котором в результате действия помех 5% сообщений не соответствуют переданным.
Определить пропускную способность симметричного бинарного канала, если вероятность ложного приёма рл = 0,02, 0 = 1 = 1 мсек.
Чему равна пропускная способность симметричного канала, если источник вырабатывает со скоростью 2 знака в секунду сообщения, закодированные кодом с основанием m = 10, а вероятность ложного приёма рл = 0,03?
Канал связи описан следующей канальной матрицей:
.
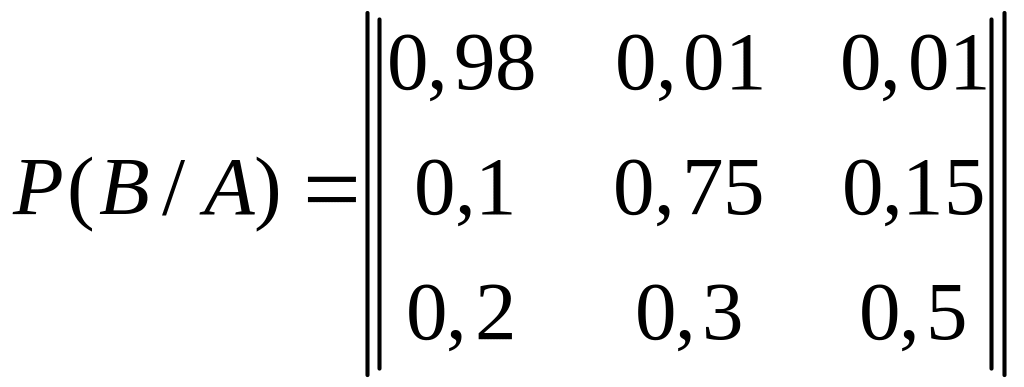Вычислите
среднее количество информации, которое
переносится одним символом сообщения,
если вероятности появления символов
источника сообщений равны
=0,7;
=0,2;
=0,1.
Чему равны информационные потери при
передаче сообщения из 1000 символов
алфавита
,
,
?
Чему равно количество принятой информации?
Источник информации выдает сообщения со скоростью
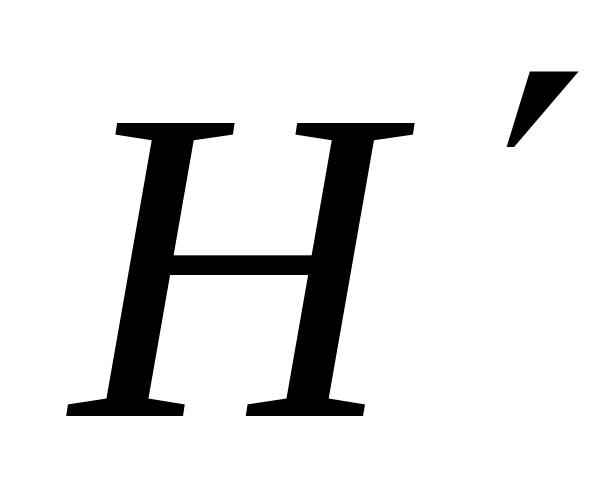= 1000 симв/сек. Алфавит состоит из трех
символов (букв) X,
Y,
Z,
статистика появления которых равна
0,7; 0,2; 0,1. Закодировать символы источника
информации таким образом, чтобы
обеспечить прохождение сообщений
через канал связи с пропускной
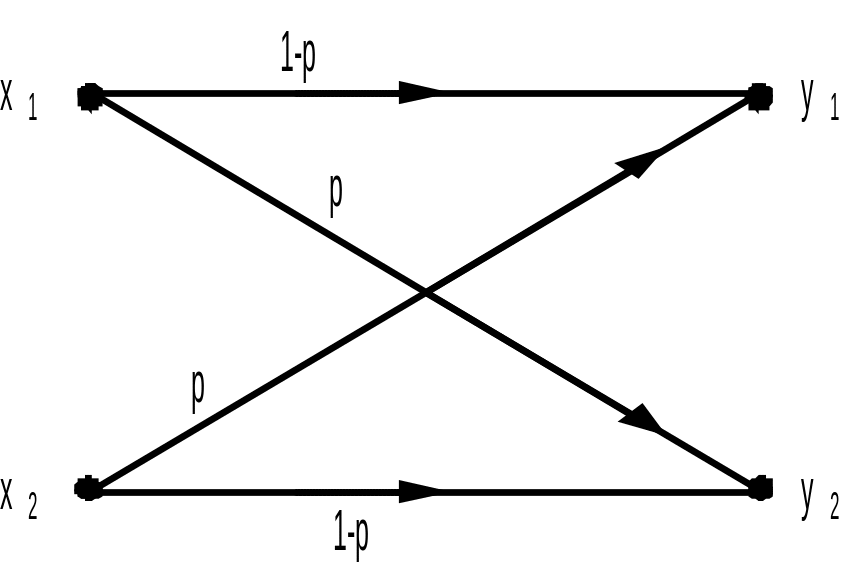
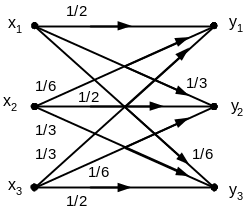
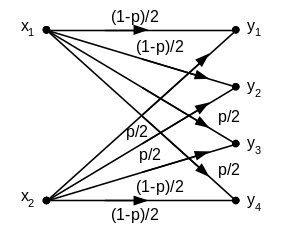
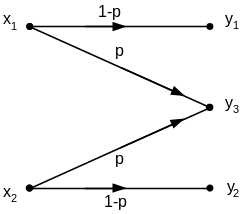
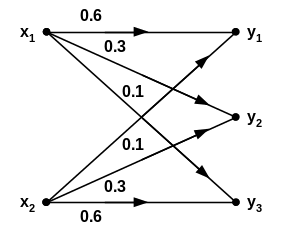
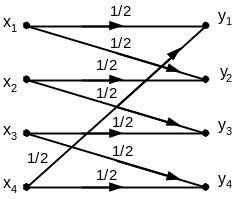
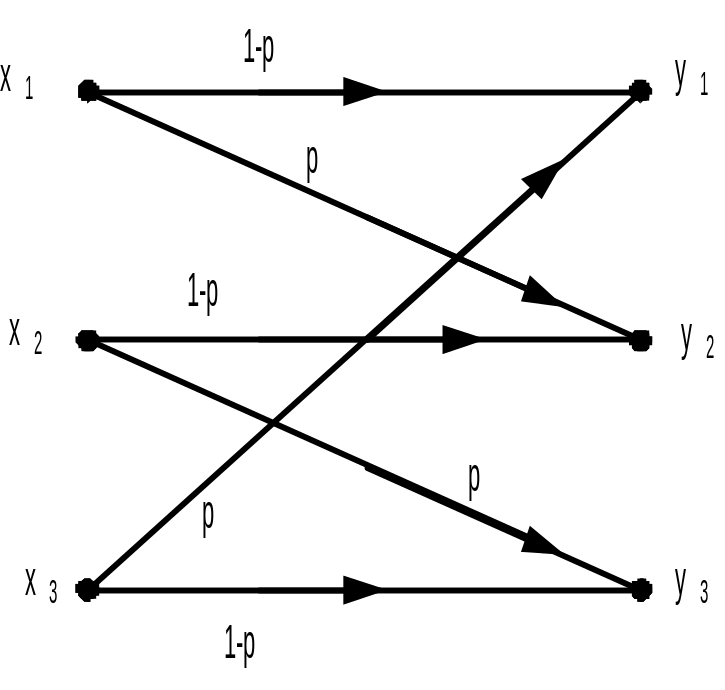
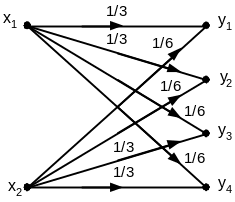
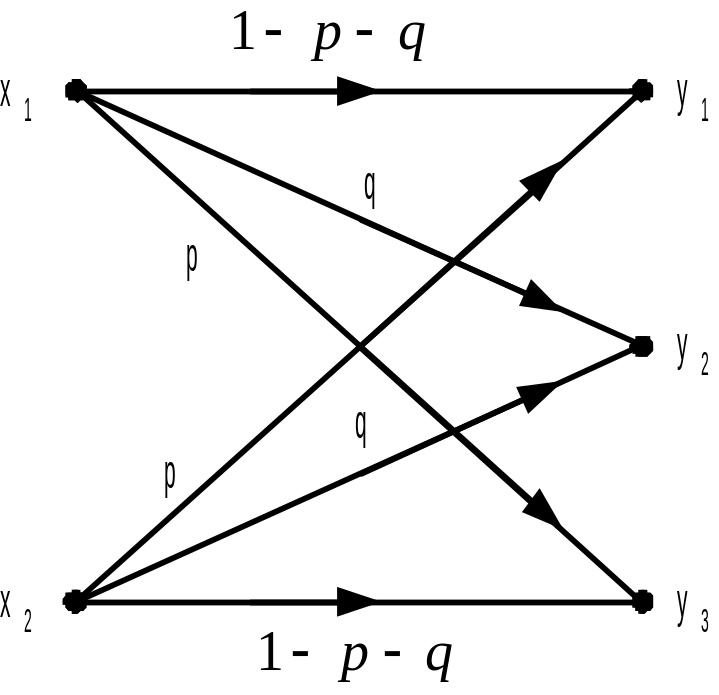
способностью С = 1250 бит/сек без задержек.Определите пропускную способность канала (рис.1.1). Символы на входе канала считать равновероятными.
а) |
|
е) |
|
б) |
|
ж) |
|
в) |
|
з) |
|
г) |
|
и) |
|
д) |
|
к) |
|
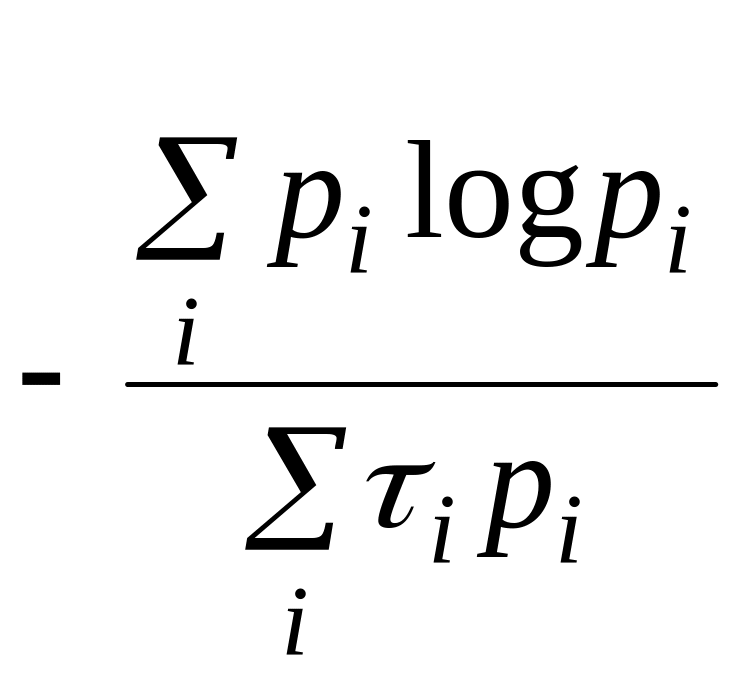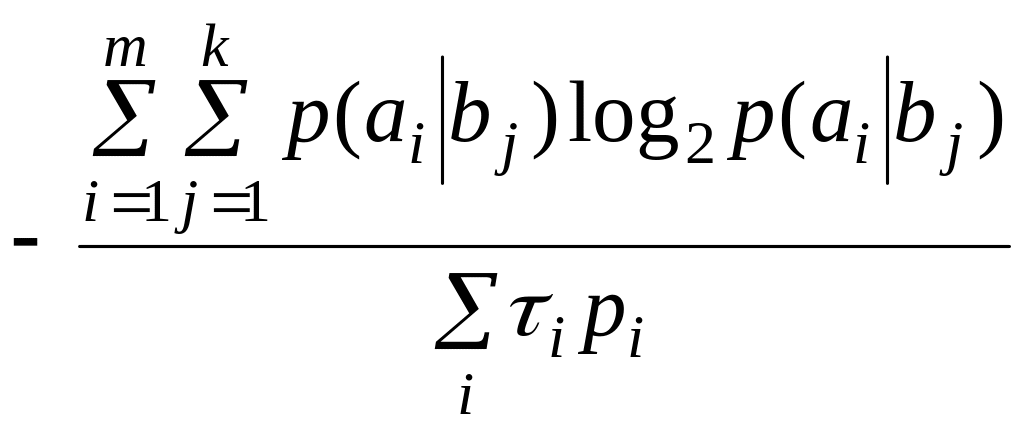