ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С. П. КОРОЛЕВА»

Кафедра эксплуатации авиационной техники

Расчетно-пояснительная записка к домашнему заданию по дисциплине

НАДЁЖНОСТЬ АВИАЦИОННОЙ ТЕХНИКИ И ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК

Расчет характеристик надежности авиационной техники

Вариант 2.34

Выполнил:

Проверил:

Оценка:

Дата:

Самара

СОДЕРЖАНИЕ

1.	Группировка данных	4
2.	Расчет эмпирических характеристик надежности	4
3.	Выбор теоретического закона распределения	4
4.	Определение параметров закона распределения	5
5.	Проверка правильности принятой гипотезы	5
6.	Определение точности оценок параметров распределения	6
7.	Построение графиков теоретического распределения	6
8.	Оценка уровня надежности	7

ЗАДАНИЕ

Наработка до отказа гидроцилиндрового (негерметичность) агрегата АУ-10 управления поворотом лопаток РНА двигателя НК-12:

2800,3600,4900,6230,7780,9000,9340,13000,14250,14870,16200,17500,19280,19800,20100, 23170,25000,26000,27500,29800.

Число наблюдаемых изделий N=350;

Число отказавших изделий r=20;

P(t)=0,8; [t]=20000 ч.

Определить закон распределения наработок до отказа.

1. Группировка данных.

Интервал наработки 0…30000 часов разбиваем на разряды по правилу Старджена:

Число разрядов принимаем равным 5 с величиной

2. Расчет эмпирических характеристик надежности.

По формулам

вычисляем в каждом разряде значения . Результаты расчетов представляются в табличном виде (табл. 1).

Таблица 1. Результаты расчетов эмпирических характеристик

№ инт.	, час	, час	, час			1/час
1	0	6000	6000	3	0,0000014285	0,0000014285	1
2	6000	12000	6000	4	0,0000019048	0,0000019212	0,9914
3	12000	18000	6000	5	0,0000023809	0,0000024295	0,98
4	18000	24000	6000	4	0,0000019047	0,0000019724	0,9657
5	24000	30000	6000	4	0,0000019047	0,000001996	0,9543

3. Выбор теоретического закона распределения.

По данным таблицы 1 строятся гистограммы эмпирического распределения (рис. 2).

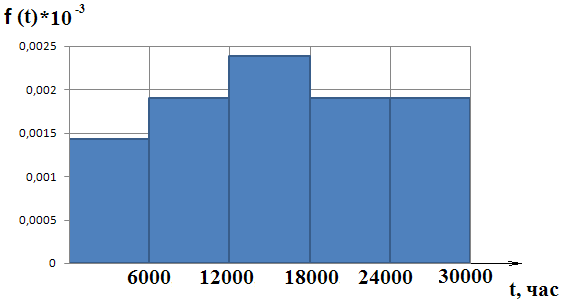
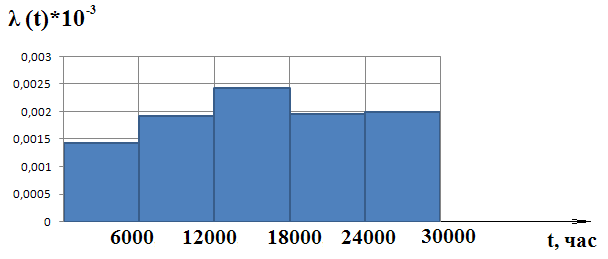
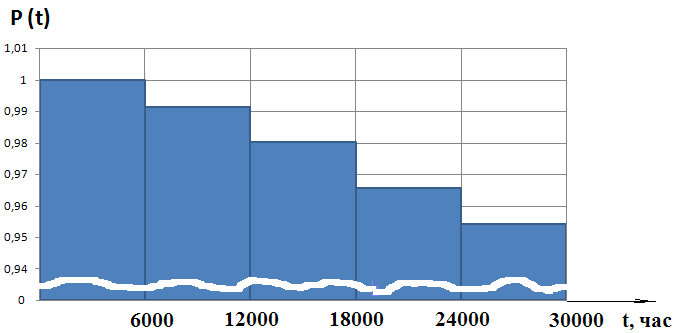
По внешнему виду гистограмм можно выдвинуть гипотезу, что отказ гидроцилиндрового агрегата управления поворотом лопаток РНА распределены по экспоненциальному закону.

4. Определение параметров закона распределения

Экспоненциальный закон распределения является однопараметрическим, т.е. для его полного определения необходимо найти один параметр – интенсивность отказов . В настоящем примере осуществлен план наблюдений [NUr], следовательно, параметр можно вычислить с использованием метода максимума правдоподобия по выражению:

Отсюда среднее время наработки до отказа

5. Проверка правильности принятой гипотезы

Осуществляется с помощью критерия Пирсона , рассчитанного по выражению

где – теоретическая вероятность отказа в интервале .

Число разрядов при расчете критерия на единицу больше числа разрядов разбиения вариационного ряда k, так как добавляется интервал от . Результаты расчетов представлены в табл. 2.

Таблица 2

Расчет критерия Пирсона

№ инт.	, час	, час	, час
1	0	6000	6000	3	0,011708	4,09781	-1,09781	0,5401115
2	6000	12000	6000	4	0,011571	4,049832	-0,04983	0,54651
3	12000	18000	6000	5	0,011435	4,002417	0,997583	0,5529844
4	18000	24000	6000	4	0,011302	3,955557	0,044443	0,5595354
5	24000	30000	6000	4	0,011169	3,909245	0,090755	0,5661641
6	30000				0,942815	329,9851	-329,985	0,0067072

Величина рассчитывается по выражению:

.

Число степеней свободы r в случаи шести разрядов таблицы и одного параметра закона распределения в соответствии с , где s – число параметров закона распределения: r=6-1-1=4.

Задавшись уровнем значимости α=10%, по таблице в зависимости от P=1-α=90% и числа степеней свободы r=4 находим критическое значение . Подсчитанное значение не попадает в критическую область (7,78; +∞),следовательно, принятая гипотеза об экспоненциальном законе распределения не противоречит статистическим данным.

6. Определение точности оценок параметров распределения.

Верхнюю и нижнюю границы доверительного интервала для параметра вычисляем по формулам:

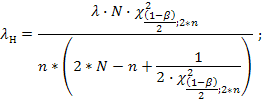
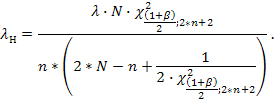
Для доверительной вероятности β=90% и n=24 найдем значения и , т.е. значения , соответствующие доверительной вероятности и соответственно и числу степеней свободы 2n=40 и 2n+2=42:

;

Подставив найденные значения, получим:

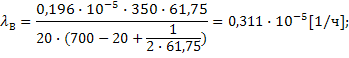
Таким образом, интервал с доверительной вероятностью 90% покрывает истинное значение параметра .

7. Построение графиков теоретического распределения.

Построение графиков распределения производим для диапазона 0 < t < 30000 часов. Вычиления производим по формулам :

Расчетные данные сведены в таблицу 3.

Таблица 3

Расчет теоретических характеристик

t, час	6000	12000	18000	24000	30000
1/час
	1,937	1,914	1,892	1,869	1,848
	0,992	0,984	0,976	0,968	0,961
	0,988	0,977	0,965	0,954	0,943
	0,981	0,963	0,945	0,928	0,910

Графики теоретического распределения показаны на рисунке 2.

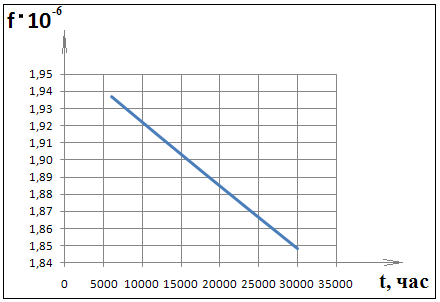
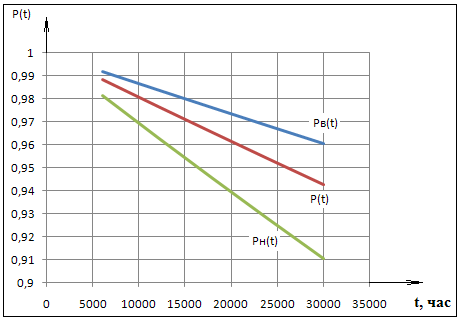
Рисунок 2 – Графики теоретического распределения

8. Оценка уровня надежности.

Конечным результатом является сравнение фактических значений характеристик надежности с нормативными величинами. В качестве нормативных величин можно выбрать либо гаммо-процентную наработку отказа, либо коэффициент .

Гамма-процентная наработка - это наработка, в течении которой изделие прорабатывает до первого отказа с вероятностью γ, выраженной в процентах.

Для анализа надежности можно принять допустимую вероятность отказа

Q(t=1)= , а вероятность безотказной работы P(t=1)=0.9999 и, соответственно, γ=99,99%. В этом случае величина должна быть не менее 1 часа.

По условию: . Подставив численные значения, получим:

Таким образом гамма-процентная наработка гидроцилиндрового агрегата удовлетворяет требованиям надежности и безопасности полетов.

Коэффициент равен числу отказов, приходящихся на 1000 часов наработки изделия. Он определяется выражением: , где - среднее время наработки до отказа элемента, агрегата или системы.

Существуют нормативные значения для каждого типа самолета для основных деталей, узлов и агрегатов всех функциональных систем. За контрольный уровень коэффициента принимается значение, равное 0,2. Оценка уровня надежности сводится к сравнению фактического и нормативного значений этого коэффициента.

При сравнении с контрольным значением видим, что изделие удовлетворяет требованиям надежности.

Как видно из графика зависимости P(t) (рис.2) точка с координатами P(t)=0,8; [t]=20000 ч не попадает в зону между , значит, расчеты не удовлетворяют нормативным требованиям.

8