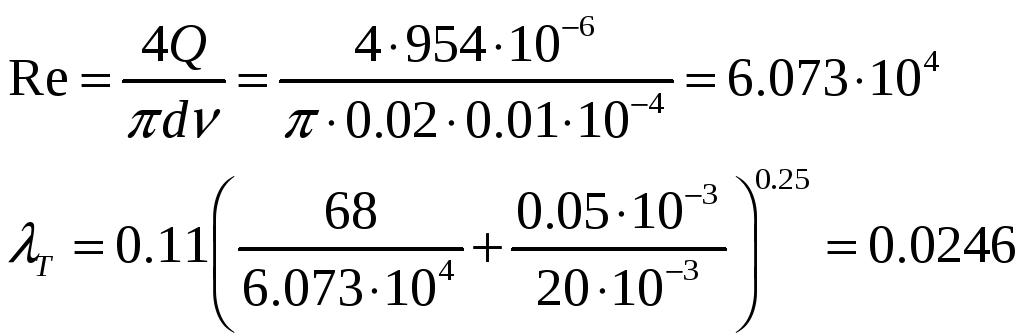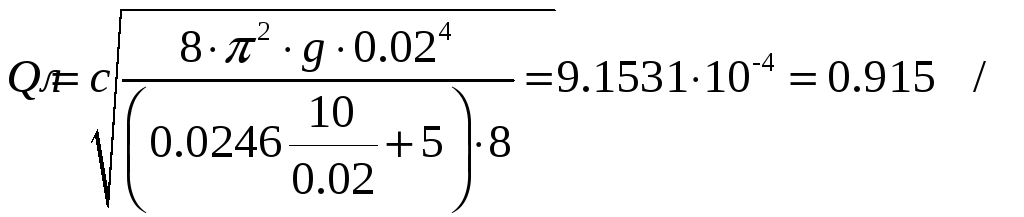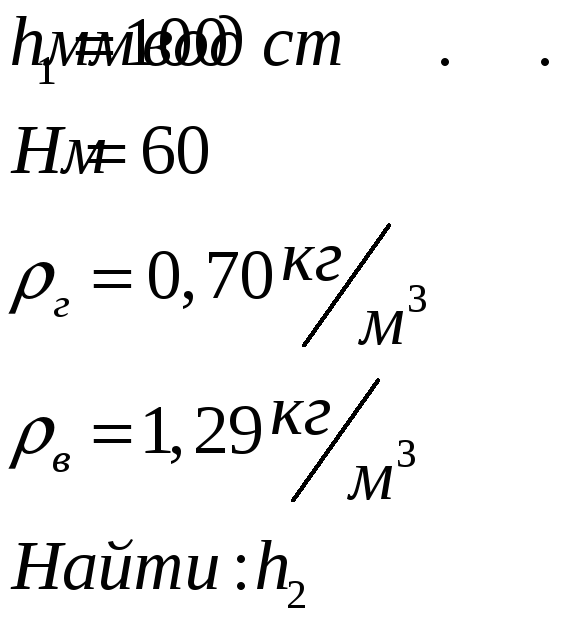Самарский Государственный Аэрокосмический Университет имени академика С.П. Королёва

Кафедра Аэрогидродинамики

Домашнее задание

Вариант №17

Выполнил:

студент группы 331

Проверил преподаватель:

Васильев В.В.

Самара 2009

З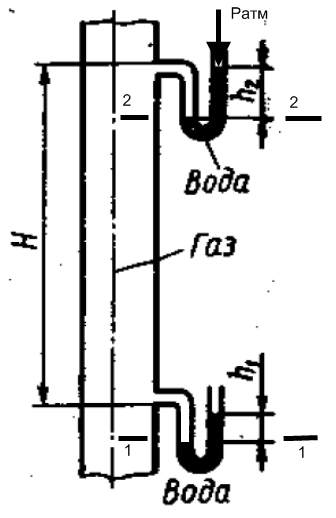адача 1.22

Дано:

Решение: 

Запишем основное уравнение гидростатики для газа для сечений 1 и 2

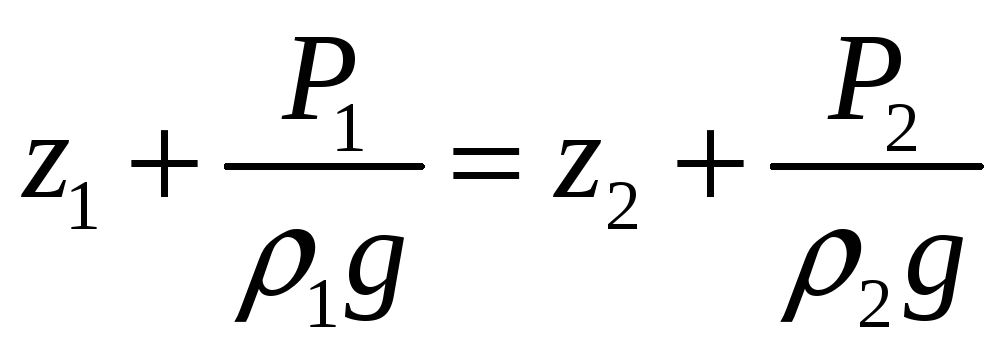
Для газа в нашем случае

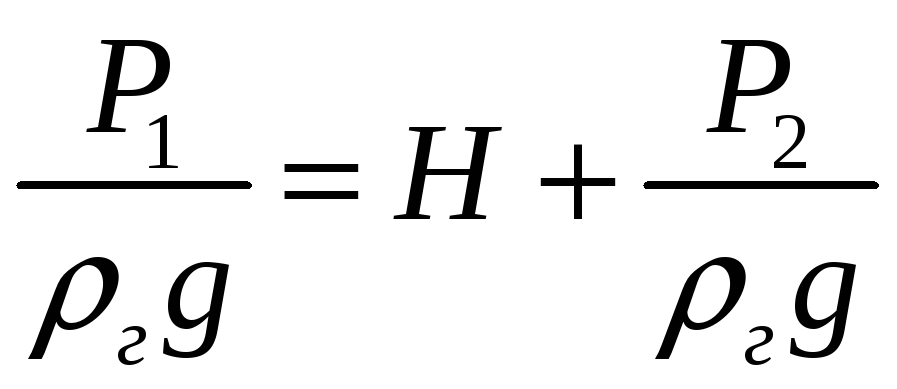
Подставим и через пьезометрические высоты воздуха и воды в трубке.

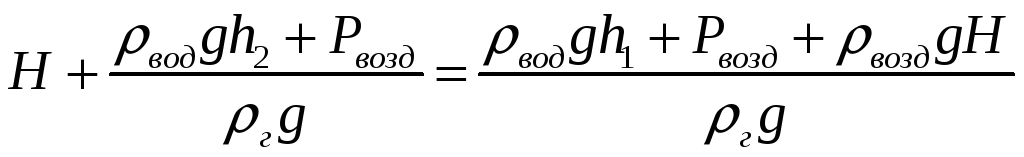
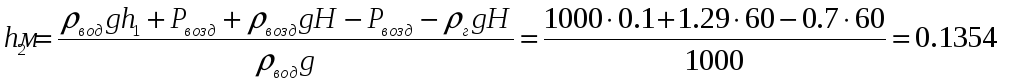
Задача 1.13

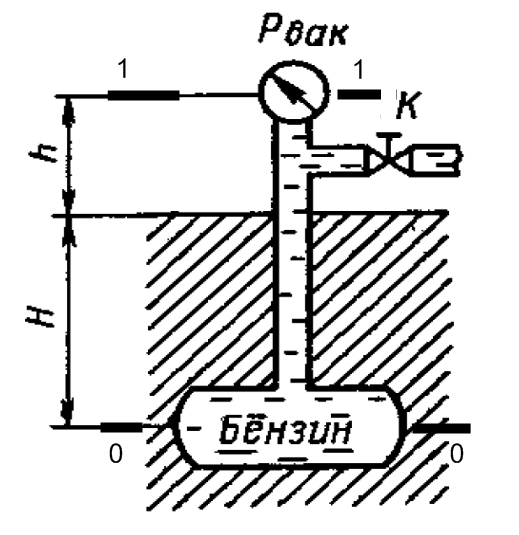
Дано:

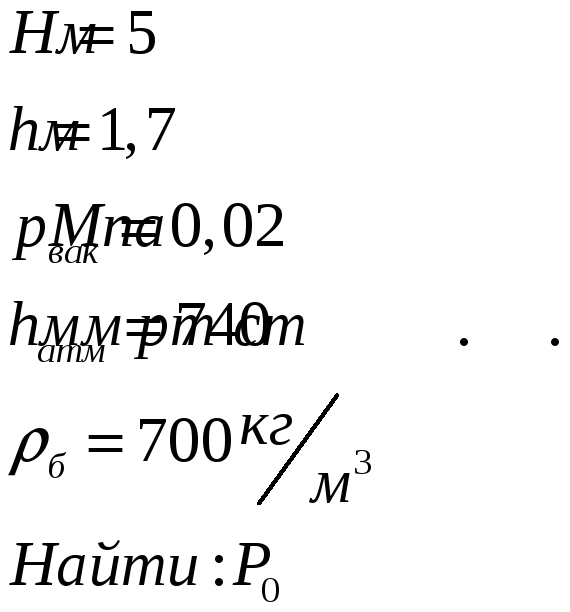
Решение:

Запишем основное уравнение гидростатики:

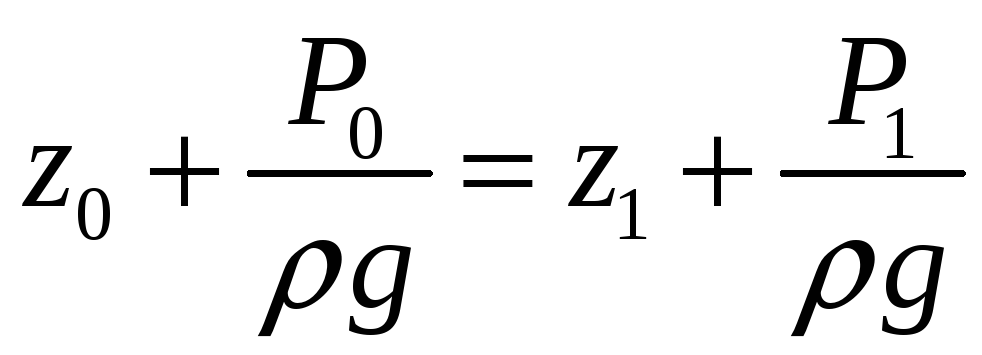
В нашем случае:

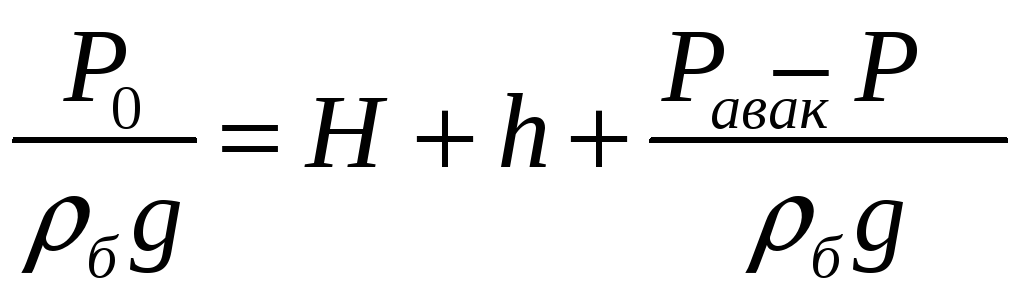
З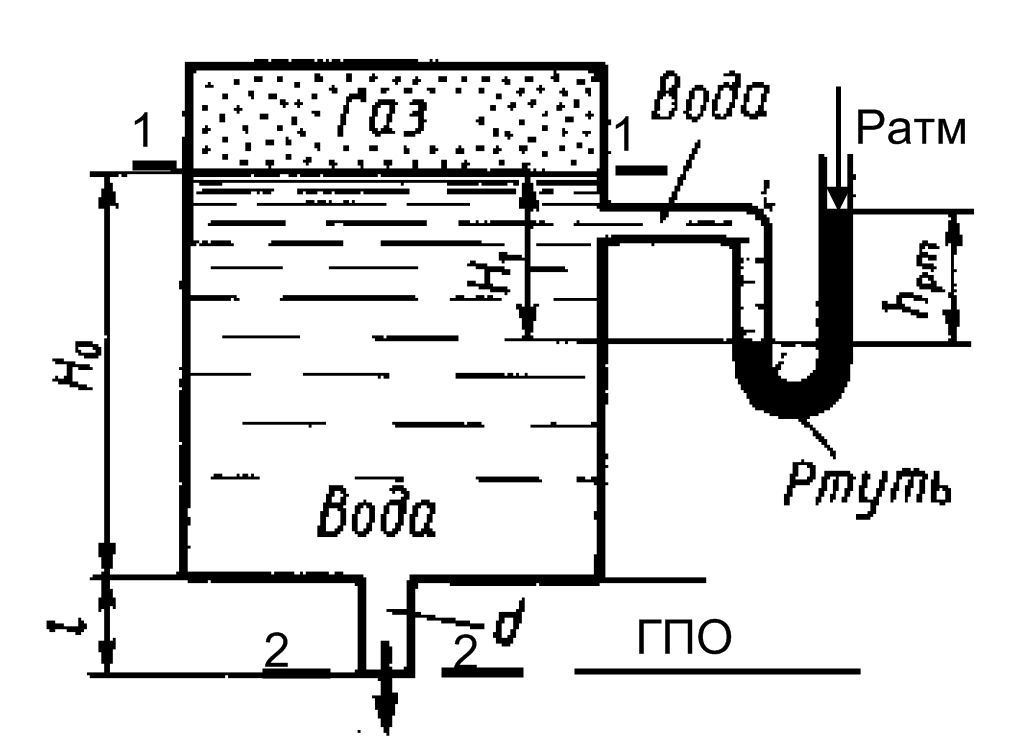адача 2.13

Дано

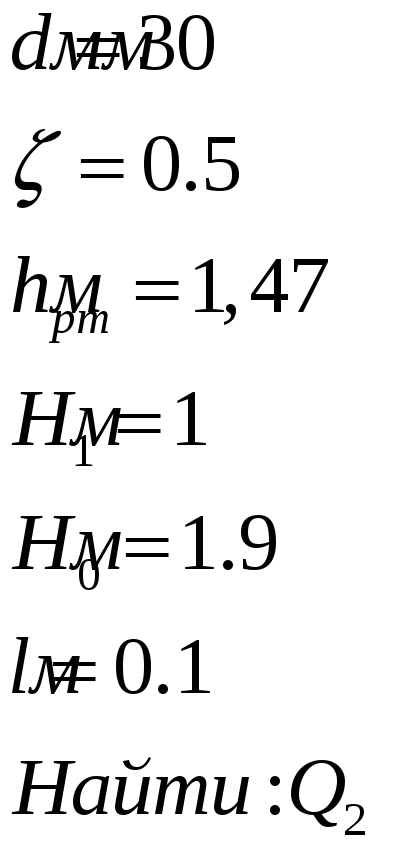
Решение:

Запишем уравнение Бернулли для сечений 1 и 2:

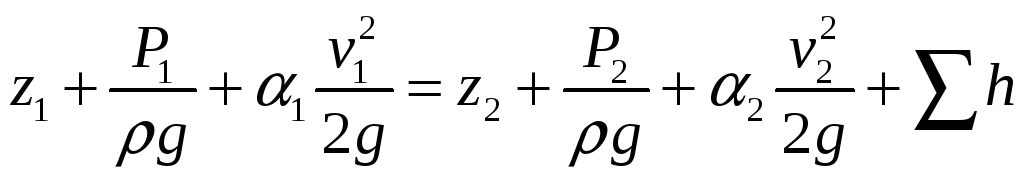
По условию задачи:

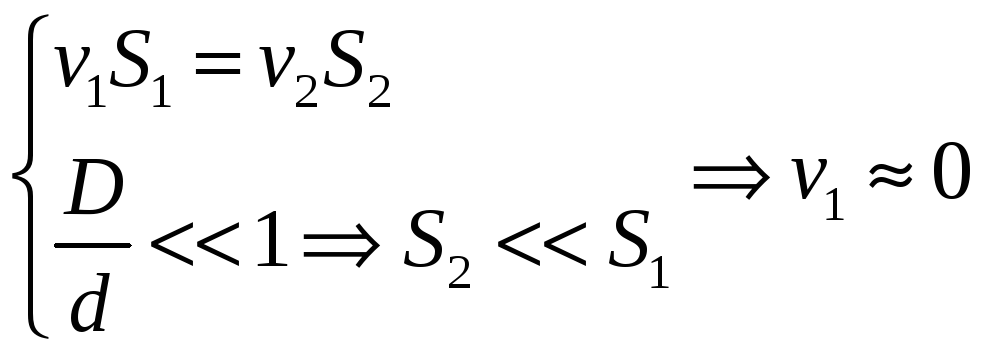
Найдем давление газа в баке с покоящейся жидкостью из уравнения

гидростатики для трубки с покоящейся жидкостью:

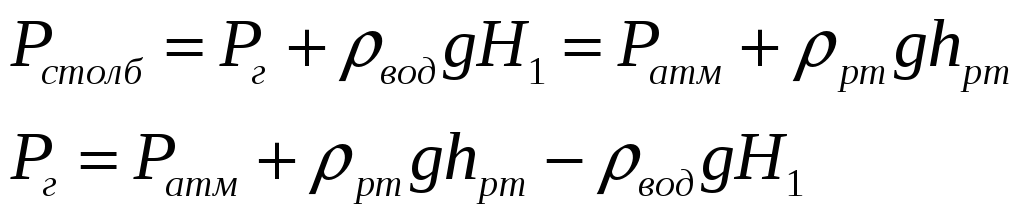
Запишем уравнение Бернулли для сечений 1 и 2 в нашем случае, принимая поток в насадке турбулентным, коэф-т Кориолиса равным 1.

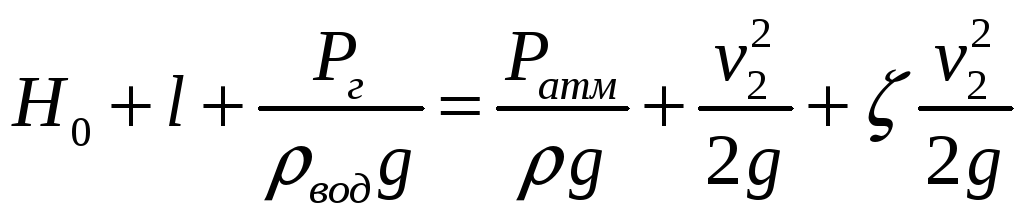
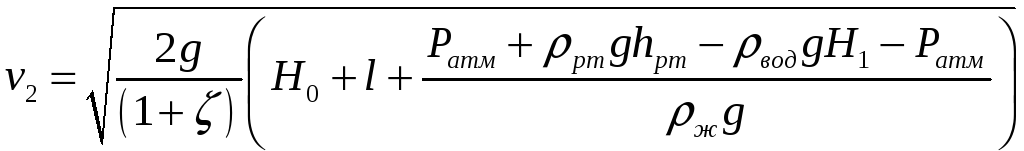
Расход через насадок:

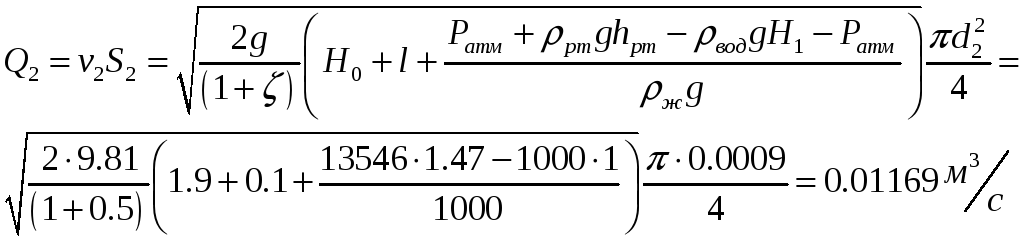
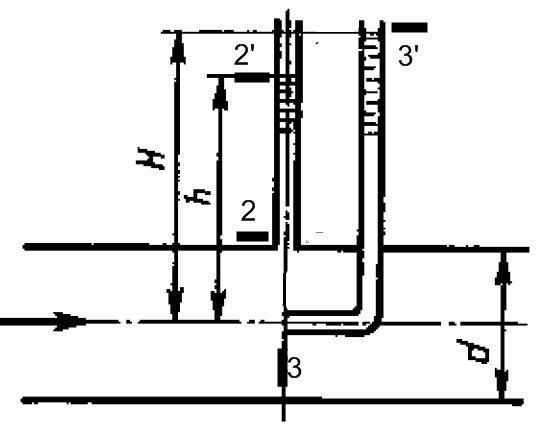
Задача 2.22

Дано

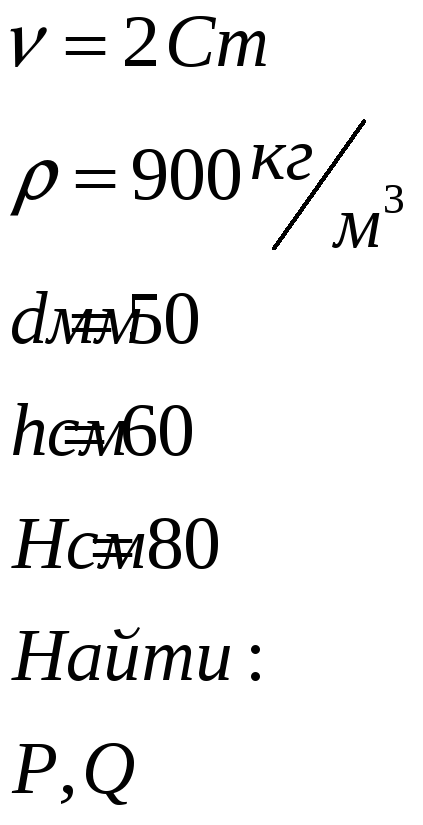
Решение:

Этой задаче трубка Пито позволяет измерить пьезометрическую высоту и скоростной напор (по скорости V_max), а пьезометр - только пьезометрическую высоту, т.к скорость перпендикулярная сечению отсутствует.

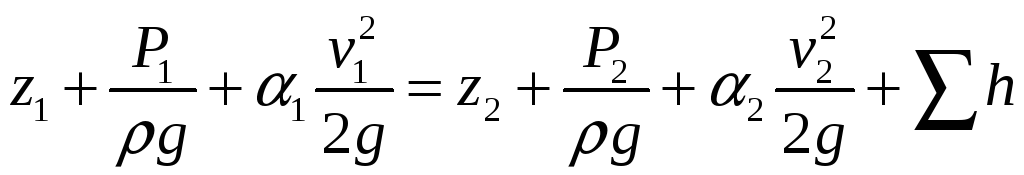
Для пьезометра:

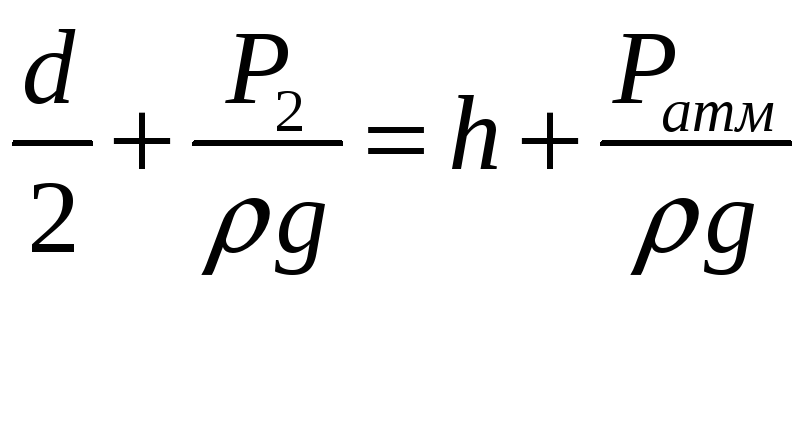, отсюда 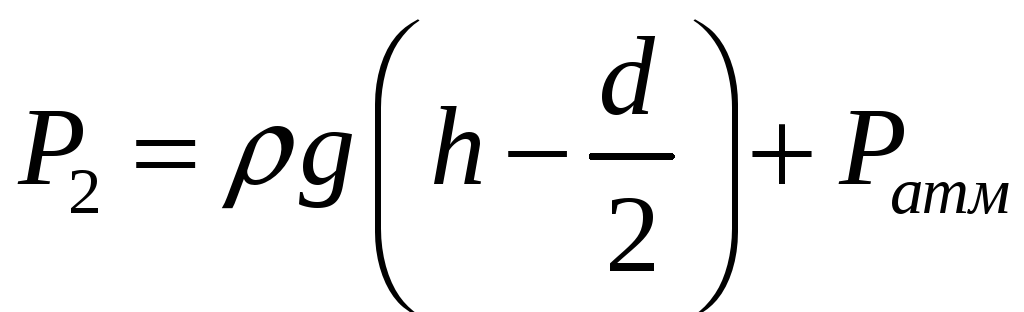, избыточное давление в трубе

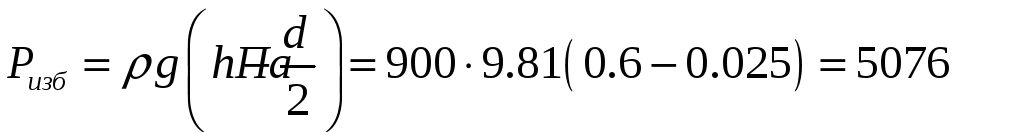
Для трубки Пито:

Пренебрегая давлением столба жидкости между сечением 2 и насадком трубки Пито, получаем уравнение Бернулли:

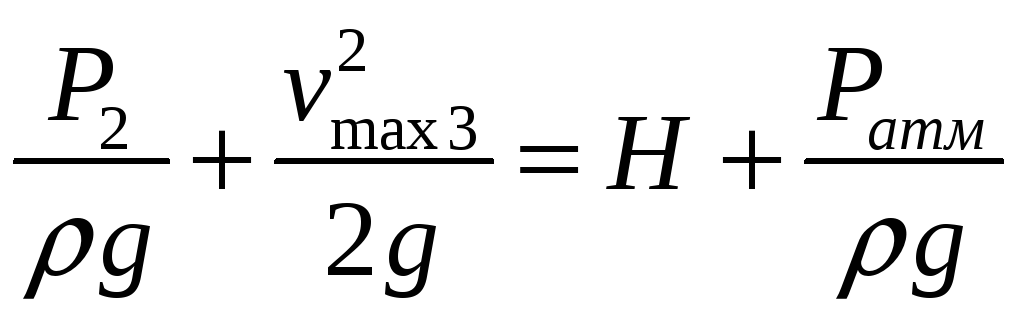
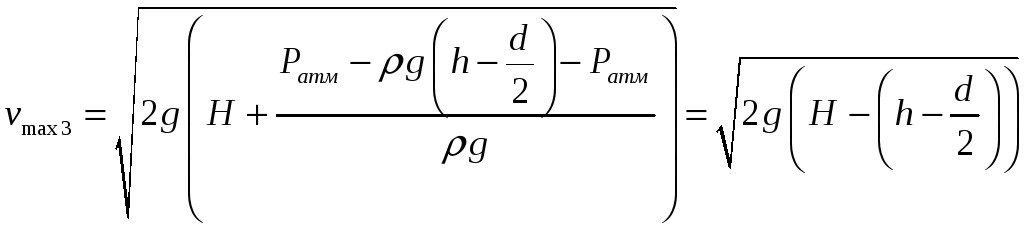
В нашем случае, мы имеем вязкую жидкость и ламинарный поток в трубе (), 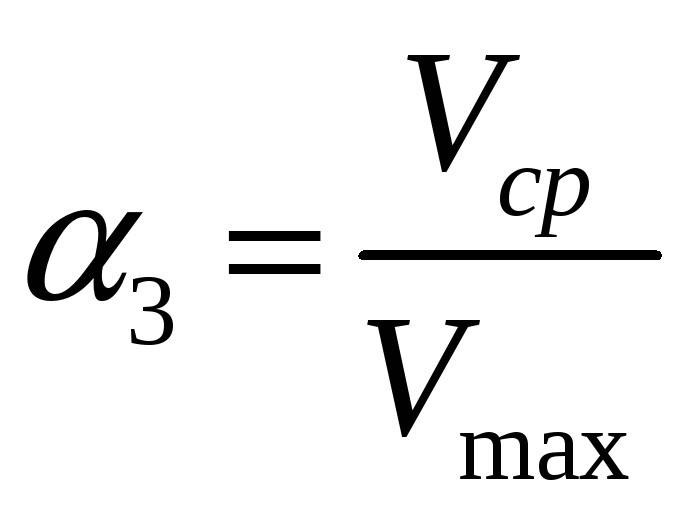=0,5

Расход жидкости в сечении с трубкой Пито равен:

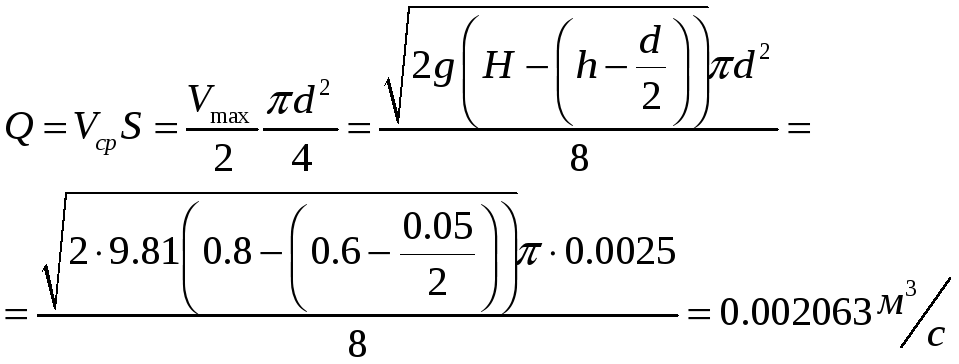
Задача 3.13

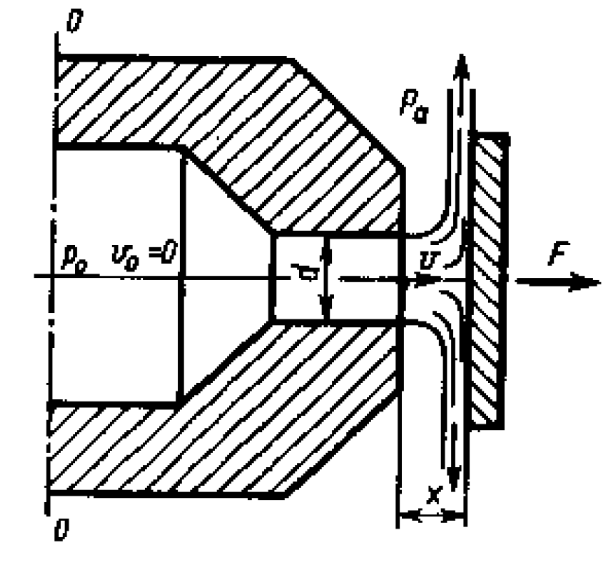
Дано

Решение

1. При прислоненной заслонке на нее действует статическое давление (V=0)

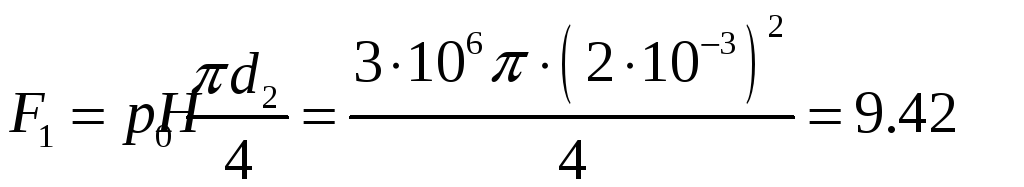
2. Для случая x>0 применим II закон Ньютона:

Выразим силу F:

Найдем скорость v:

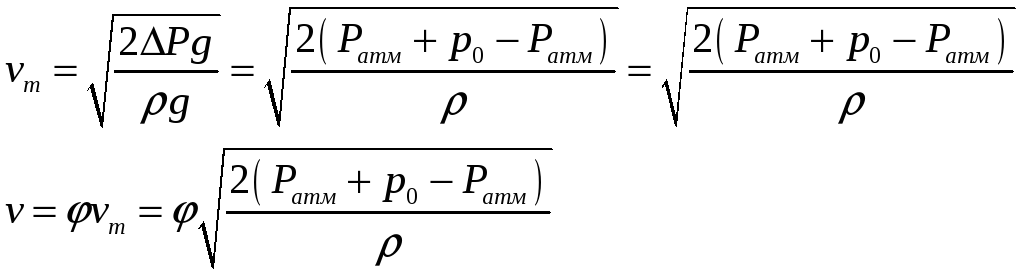
Найдем расход G:

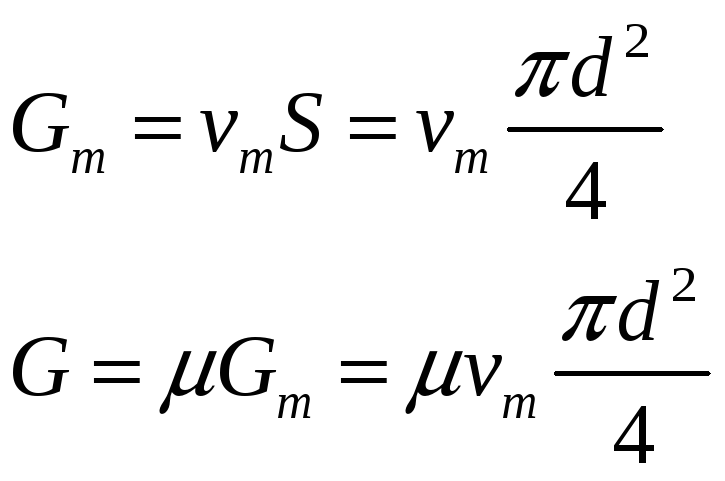
Сила F₂:

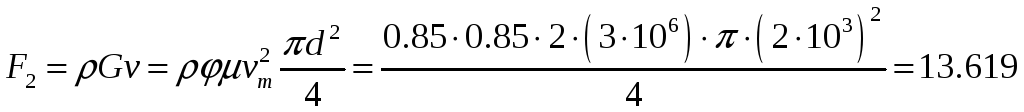
При

Отношение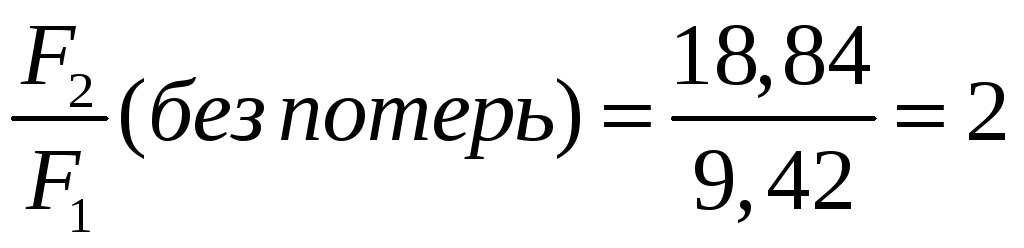

З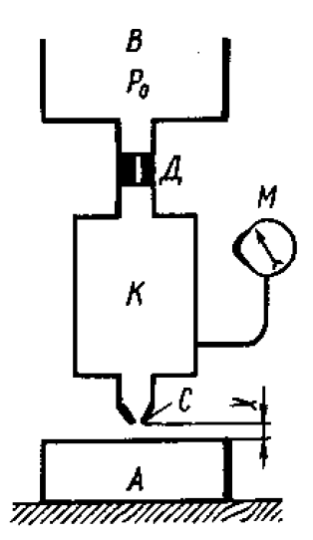адача 3.22

Дано

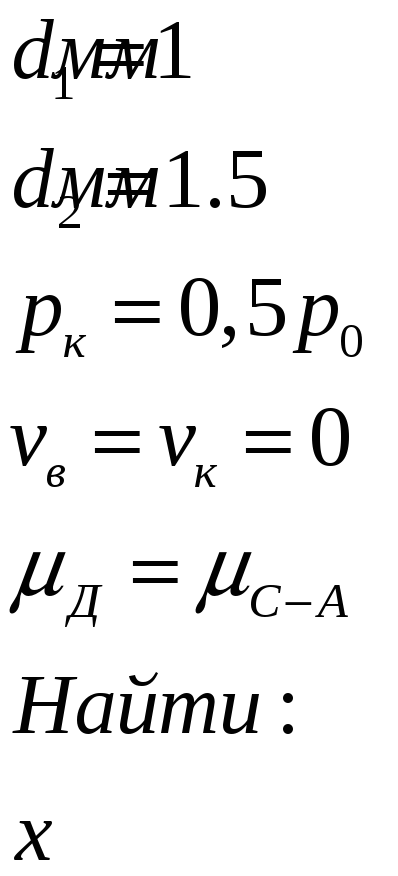
Решение:

Зададимся равенством расходов в жиклере Д и сопле С-А:

Найдем скорость на выходе из жиклера Д, используя уравнение Бернулли:

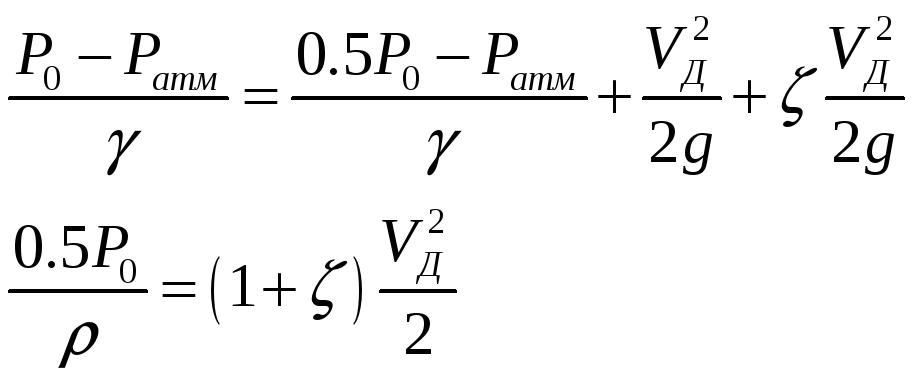
Отсюда V_д:

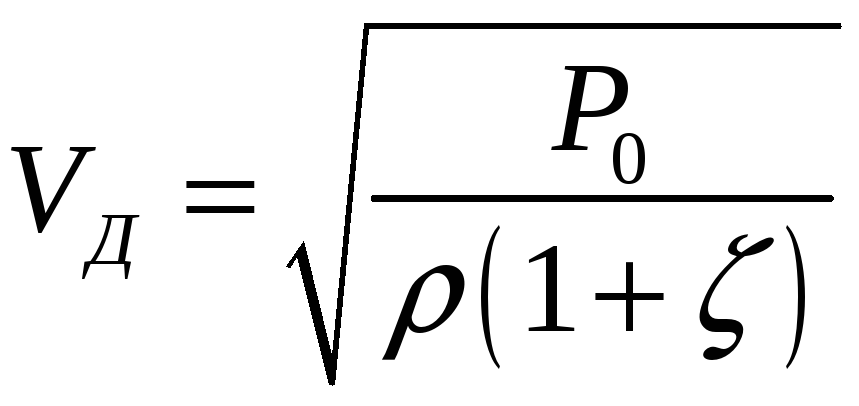
Найдем скорость на выходе из сопла С-А, приняв равенство коэффициентов на основании равенства коэф-тов расхода:

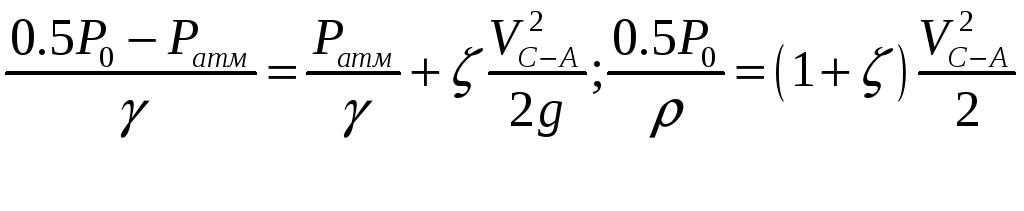
Отсюда V_С-А:

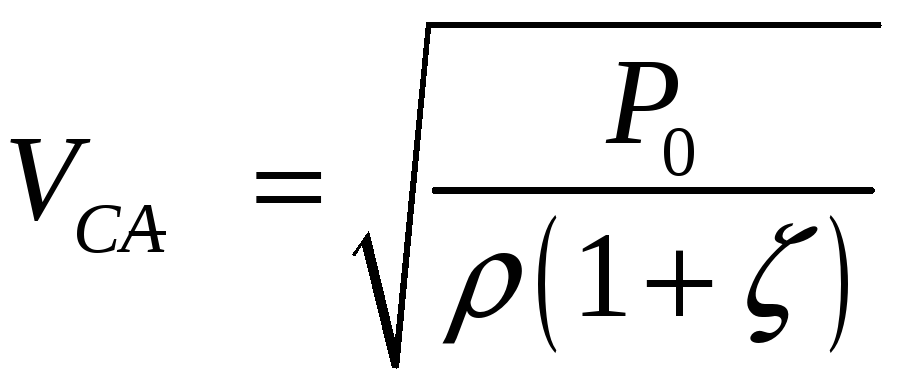
Запишем уравнение постоянства расхода в соответствии с найденными величинами, записывая площадь выходного сечения как площадь цилиндрической поверхности:

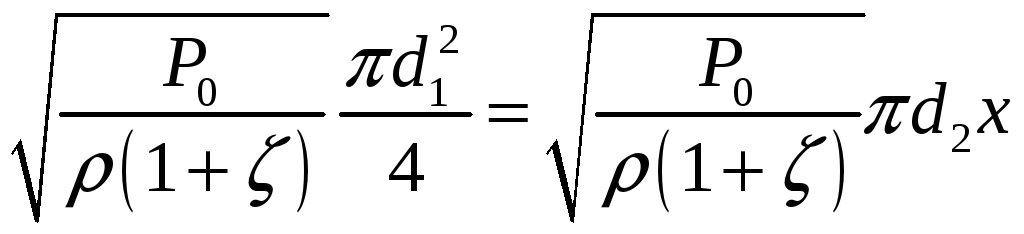
Отсюда

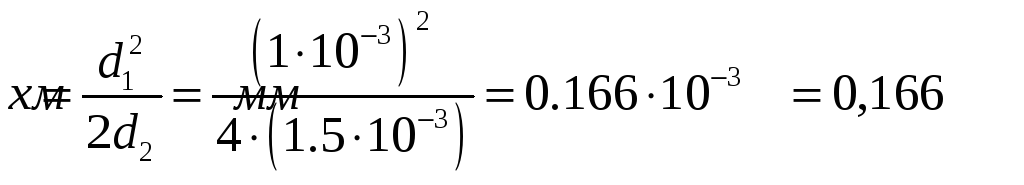
Задача 4.13

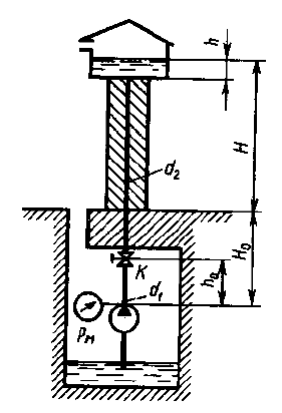
Дано

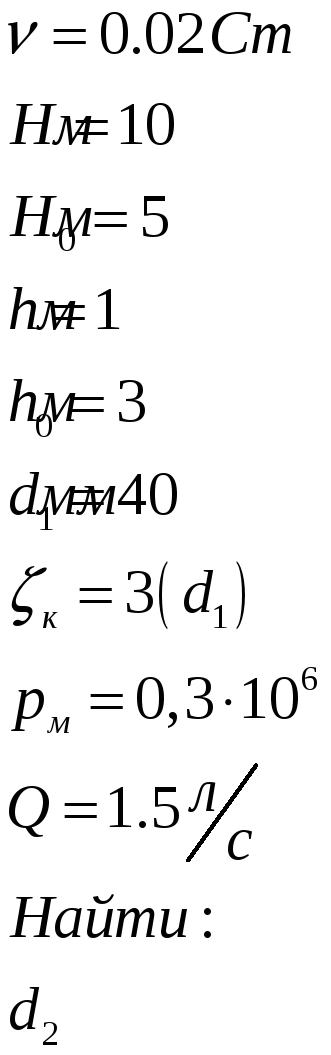
Решение:

Найдем число Re для диаметра d₁:

, имеем турбулентный режим течения, зададимся турбулентным режимом также во второй трубе (d₂)

Необходимо обеспечить условие:

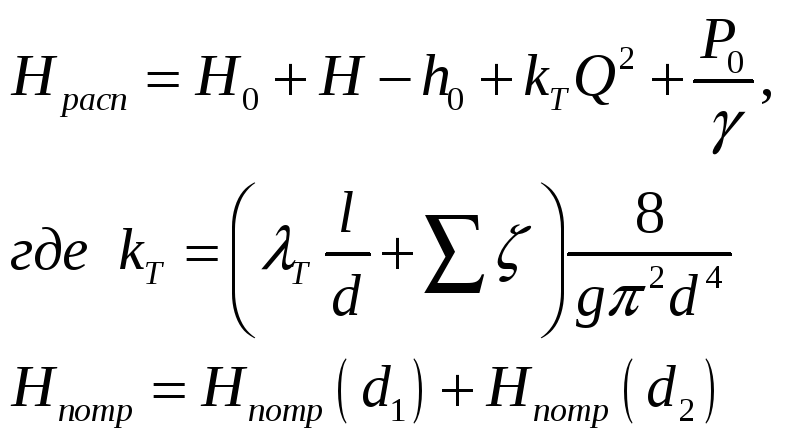
Выразим потребный папор во втором трубопроводе:

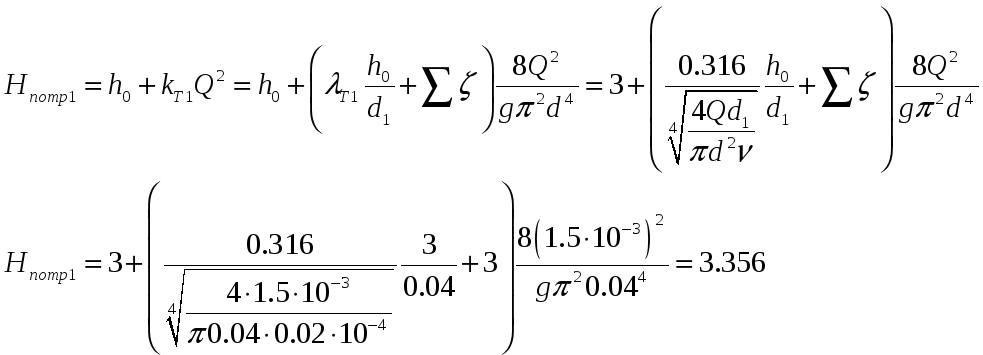
Потребный напор во втором трубопроводе:

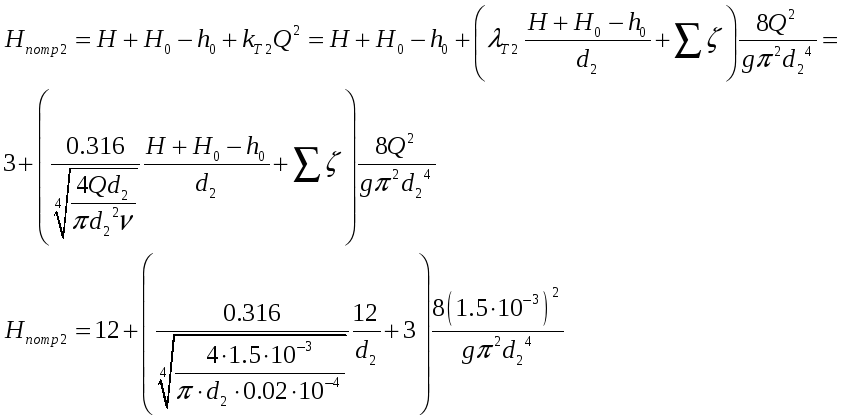
Таким образом, имеем условие:

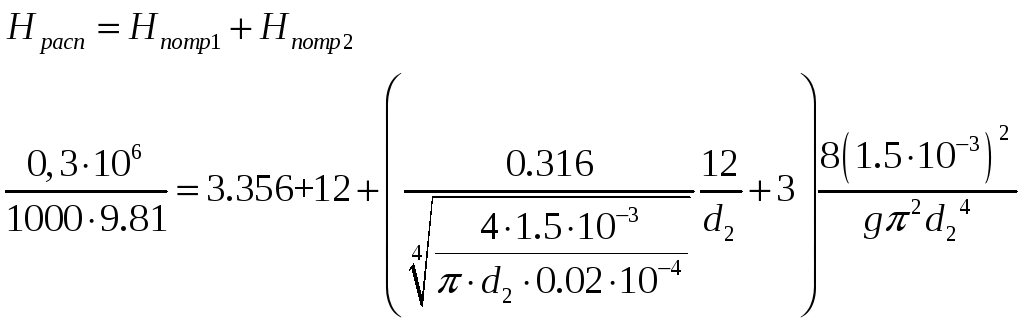
Решение находим численно, с помощью метода итераций. Для этого задаемся рядом значений , по которым приближенно строим функцию . Затем на этой кривой отмечаем точку и находим значение , соответствующее располагаемому напору от насоса (наш случай). Для точности построим график с помощью пакета Mathcad.

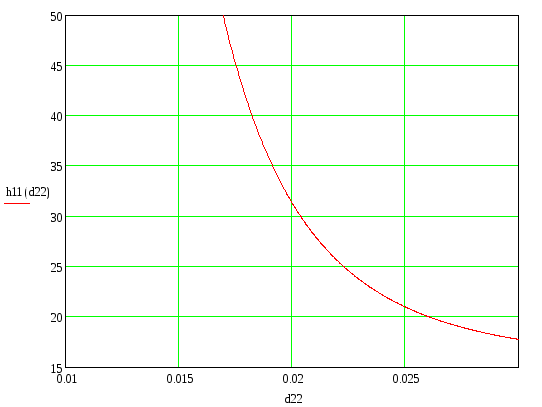
Отсюда =0,02 м

Задача 4.22

Дано

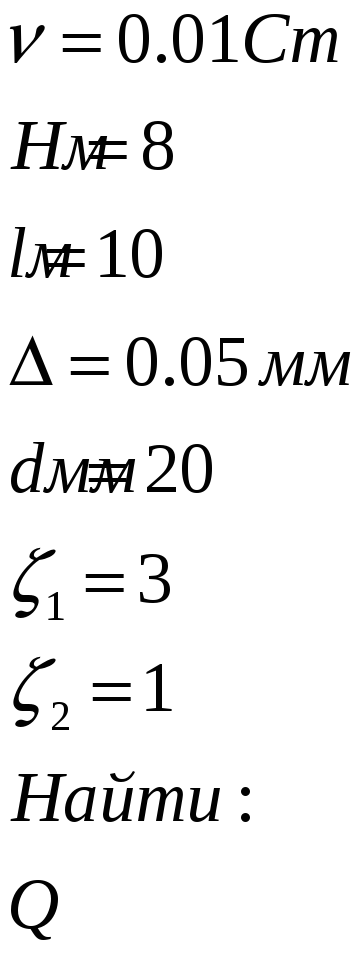
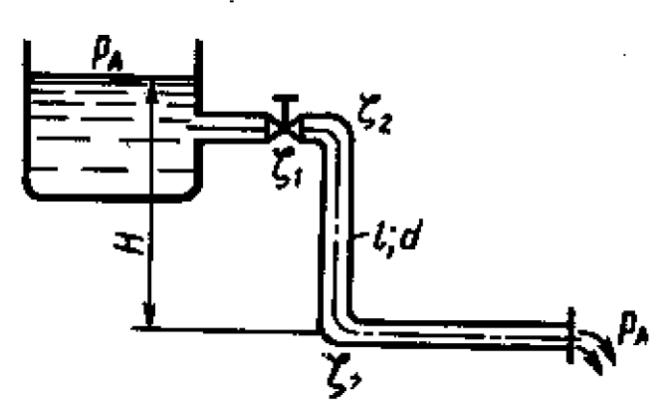
Решение:

Уточним режим течения жидкости в трубе, для этого зададимся критическим значение числа Рейнольдса, найдя тем самым скорость потока в трубе:

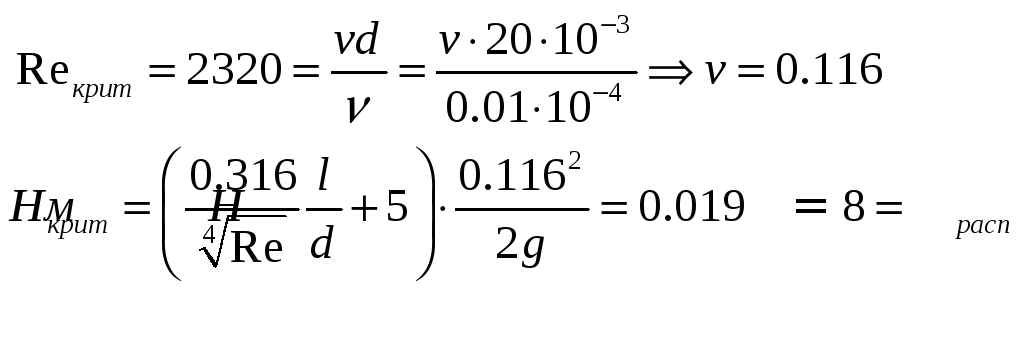
Таким образом, имеем турбулентный режим.

Для нахождения в первом приближении примем

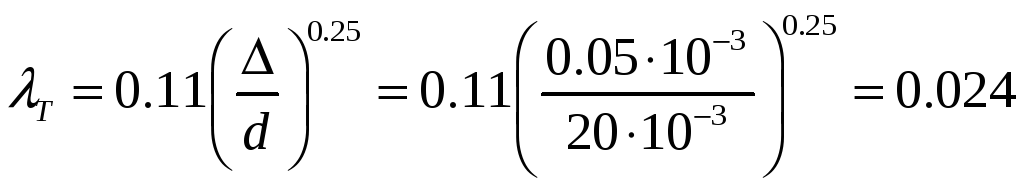
Найдем расход при этом

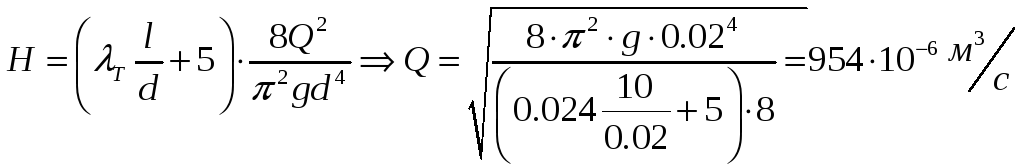
Найдем уточненное значение , учтя число Рейнольдса: