1.3 Диаграммы Эйлера-Венна

Диаграммы Эйлера-Венна — геометрические представления множеств.

Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него – кругов (или каких–либо других замкнутых фигур), представляющих множества. Круги могут пересекаться в случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Приведенные на рис. 2.2 – 2.6 иллюстрации операций объединения, пересечения, дополнения, обычной и симметрической разности двух множеств являются диаграммами Эйлера-Венна.

Попробуем представить множество диаграммой Эйлера-Венна.

Построим общую диаграмму, показанную на рис. 2.8,а. Прямоугольник – универсальное множество U. Круги – множества A, B, C.

Р исунок 2.8 – Диаграммы к Примеру 1

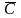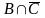Заштрихуем В диагональными линиями в одном направлении, а – в другом (рис. 2.8,б). Площадь с двойной штриховкой представляет собой их пересечение, т.е. множество . Выделим это множество цветом. На новой копии диаграммы заштрихуем эту область линиями одного направления, a A — другого. Вся заштрихованная на рис. 2.8,в область представляет объединение множеств А и , т.е. множество . Выделим эту область цветом.

1.4 Основные законы и тождества алгебры множеств

Основные законы алгебры множеств (булевой алгебры множеств) представляются в виде тождеств, в которых участвуют символы обозначений множеств, включая символы универсального и пустого множеств, и символы операций объединения, пересечения и дополнения.

Ассоциативный закон:

(X Y) Z = X (Y Z) = X Y Z

(X Y) Z = X (Y Z) = X Y Z

Коммутативный закон:

X Y = Y X

X Y = Y X

Закон идемпотентности (повторения):

X X = X

X X = X

Дистрибутивный закон:

(X Y) Z = (X Z) (Y Z)

(X Y) Z = (X Z) (Y Z)

Законы универсального U и пустого множеств (законы нуля и единицы 0, U 1):

X = X

X =

X U = U

X U = X

= U

= .

Законы исключенного третьего и противоречия:

X 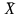= U

X =

Законы де Моргана:

Закон двойного отрицания:

= X.

При работе с множествами могут оказаться полезными тождества, приведенные ниже. Однако они требуют доказательства. Доказать их можно, используя основные законы.

Дистрибутивный закон пересечения относительно разности:

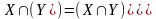
Дистрибутивный закон пересечения относительно симметрической разности:

Дистрибутивный закон разности относительно пересечения:

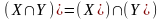
Дистрибутивный закон разности относительно объединения:

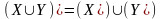
Дистрибутивные законы объединения и пересечения относительно разности:

X\(Y Z) = (X\Y) (X\Z)

X\(Y Z) = (X\Y) (X\Z)

Представление пересечения и объединения через разность:

X Z = X\(X\Z)

X Y= (X\Y) (Y\X) (X Y) = (X\Y) (Y\X) X\(X\Y)

Законы нуля и единицы для разности:

(X \Y) (X Y) =

X \ = X \U =

\X =

U\X =

X \X = U

Законы поглощения:

Закон склеивания:

Свойства симметрической разности:

,

,

,

,

,

.