МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ––––––––––––––––––––– ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ “МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ” ––––––––––––––––––––– Кафедра “Персональные компьютеры и сети” Смирнов А.М. Дискретная математика Учебное пособие Москва 2014

УДК: 519.1(075.8)

Рекомендовано в качестве учебно-методического пособия редакционно-издательским советом МГУПИ

Рецензенты:

д.т.н., профессор Михайлов Б.М.

Смирнов А.М. Дискретная математика: Учебное пособие. - М.: МГУПИ, 2014. – 69 с.

В данном пособии излагаются подробно такие разделы дискретной математики, как основы теории множеств и основы теории графов. Может быть использовано при выполнении лабораторных и домашних работ, курсовых и дипломных проектов.

Учебное пособие предназначено для подготовки студентов всех форм обучения по направлению 230100 «Информатика и вычислительная техника» профиль 230100.01 «Вычислительные машины, комплексы, системы и сети» по дисциплине «Дискретная математика». Пособие может быть полезно для начинающих пользователей, студентов, преподавателей.

Библиограф.: 8 названий.

 Смирнов А.М.

Содержание

Введение …………………………………………………………………………………………………4

1 Множества …………………………………………………………………………………………..5

1.1 Способы определения множеств……………………………………………………5

1.2 Операции надо множествами………………………………………………………...7

1.3 Диаграммы Эйлера-Венна……………………………………………………………..10

1.4 Основные законы и тождества алгебры множеств……………………….11

1.5 Доказательства тождественности формул…………………………………….12

1.6 Соответствия и их свойства…………………………………………………………..13

1.7 Функция, функционал, оператор…………………………………………………..15

1.8 Отображения, преобразования и перестановки……………………………19

1.9 Отношения……………………………………………………………………………………..20

Введение

Дискретная математика изучает математические модели объектов, процессов и зависимостей, с которыми имеют дело в технике, биологии, социологии и других областях деятельности человека. Их особенность – дискретный и как правило, конечный характер. Это ограничивает возможность использования моделей и методов классической непрерывной математики. Поэтому дискретная математика – самостоятельное направление современной математики.

Дискретная и непрерывная математика взаимно дополняют друг друга. Понятия и методы одной часто используются в другой. Например, системы линейных уравнений как модели непрерывной математики характеризуются конечным множеством линейно независимых уравнений и при определенных условиях конечным множеством решений.

Один и тот же объект может рассматриваться с двух точек зрения и в зависимости от этого выбирается непрерывная или дискретная модель. Так электрическая схема как дискретный объект может быть представлена графом – моделью ее структуры, а как непрерывный объект – вектором значений параметров элементов, соответствующих ребрам графа. На основе этих моделей получают систему линейных или нелинейных уравнений для расчетов токов и напряжений в схеме.

Классическая непрерывная математика развивалась в условиях, когда возникли и требовали решения задачи механики и физики. Дискретная математика сложилась и интенсивно развивается в связи с необходимостью решения задач управления и создания сложных технических систем. Многие задачи, возникшие в прошлом как головоломки, сегодня нашли интерпретацию как задачи управления.

Особенность большинства задач дискретной математики – возможность их решения полным перебором допустимых решений в силу конечного множества их вариантов. Однако с ростом размерности задачи простой перебор достаточно быстро становится бессильным. Для многих важных задач до настоящего времени не найдено эффективных алгоритмов решения. Поэтому ищут «хитрые» алгоритмы для упрощения перебора и определения пусть не точного, а хотя бы приближенного, но хорошего решения.

На сегодняшний день наиболее значимым направлением развития дискретной математики являются информационные технологии. Это объясняется прежде всего необходимостью создания и эксплуатации персональных компьютеров, компьютерных сетей, систем управления, а также автоматизированных средств обработки информации.

1 Множества

Множество – основное понятие в теории множеств, которое вводится без определения. О множестве известно как минимум то, что оно состоит из элементов. Принадлежность элемента множеству оценивается по наличию у него признаков, характеризующих множество.

1.1 Способы определения множеств

Множество – состоит из элементов. Принадлежность элемента а множеству М обозначается ("а принадлежит М"), не принадлежность – .

Множество А называется подмножеством множества В (обозначается 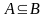), если всякий элемент из А является элементом В (рис 1.1). Если множество A является подмножеством множества B и , то А называется строгим подмножеством (обозначается , читается A включено (содержится) в B).

Рисунок 1.1 – Множество С с подмножествами В и А

Содержательные примеры множеств и их возможные обозначения:

N – множество натуральных чисел 1, 2, 3,...;

N₁ – множество натуральных чисел, не превосходящих 100;

R – множество действительных чисел.

Из рис. 2.1 видно, что если и , то . такое свойство включения называется транзитивностью.

По поводу равенства множеств можно сказать:

Множества А и В равны, если их элементы совпадают (Определение I), или множества А и В равны, если и (Определение II).

Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным (например, множества N, R – бесконечные множества).

Число элементов в конечном множестве А называется его мощностью и обозначается |А|.

Если , то |А| < |B|.

Множество мощности 0, т.е. не содержащее элементов, называется пустым (обозначается ): | | = 0. Принято считать, что пустое множество является подмножеством любого множества.

Множеством подмножеств некоторого произвольного множества U или его булеаном (обозначается (U)), называется множество, элементами которого являются все подмножества множества U. Оно включает в качестве элементов также пустое множество и само множество U.

Мощность булеана равна

| (U)| = 2ⁿ, где n = |U|.

Таким образом, если множество U состоит из n элементов, то его булеан состоит из 2ⁿ элементов.

В конечном множестве можно задать нижнюю и верхнюю границы, обозначаемые

inf A = m и sup A = M,

соответственно. Здесь A – множество, а m и M некоторые элементы множества (не обязательно числа).

Если , то inf A inf B, а sup A sup B.

Приведем способы задания множеств.

Множества можно задавать перечислением, т.е. списком своих элементов. Списком можно задать лишь конечные множества. Обозначение списка – в фигурных скобках. Например, множество А устройств домашнего компьютера, состоящего из процессорного блока a, а также периферийных устройств В (монитора b, клавиатуры с и принтера d), может быть представлено списком:

А = {а, В} или А = {а, b, с, d}.

Необходим внести следующие уточнения:

1) в списке, задающем множество, одинаковые элементы представляются одним элементом (поэтому в множествах нижняя и верхняя границы единственны).

2) перестановка элементов в списке не изменяет множество.

3) задание типа N = 1, 2, 3, ... – не список, но лишь допустимое условное обозначение.

Следующий метод задания множества – задание с помощью порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры. Например, множество всех целых чисел, являющихся степенями двойки 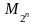, , где N – множество натуральных чисел, (допустимое обозначение = 1, 2, 4, 8, 16,...) может быть представлено порождающей процедурой, заданной двумя правилами, называемыми рекурсивными:

1) ;

2) если , то .

Последний способ задания множества, это задание описанием характеристических свойств, которыми должны обладать элементы множества. Обозначается:

М = {х|Р(х)} или М = {х:Р(х)}.

Читается так "Множество М состоит из элементов х таких, что х обладает свойством Р". Например, множество B периферийных устройств персонального компьютера может быть определено, как B = {х: х – периферийное устройство персонального компьютера}.

Надежным способом точно описать свойство элементов данного множества является задание распознающей процедуры. Она должна устанавливать для любого объекта x, обладает ли он данным свойством Р (и, следовательно, принадлежит множеству) или нет. Например, распознающей процедурой для множества А всех студентов МГУПИ, имеющих студенческие билеты университета, является проверка его наличия. Тогда множество А может быть представлено более точно: "А – множество всех студентов, имеющих студенческие билеты МГУПИ".

Другой пример: для описания характеристического свойства элементов множества всех целых чисел, являющихся степенями двойки ("быть степенью двойки"), разрешающей процедурой может служить любой метод разложения целых чисел на простые множители.

Тогда 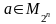, если а = 1 или если а = 2 х 2 х ... х 2 = 2ⁿ, .