Метод потенциалов для транспортной задачи с планом построенным методом минимального элемента.

Пример.

Рассмотрим план построенный методом минимального элемента из задачи предыдущей лекции. Оценим его на оптимальность методом потенциалов.

Значение целевой функции для этого плана :

План вырожден, т.к. в нем - 8, а = 4+6-1=9.Поэтому в план не обходимо будет ввести еще один базисный элемент.

Составим систему уравнений для и вычислим все потенциалы Ui и Vj . Систему выпишем из невырожденного плана

Для возможности решения системы введем уравнение для элемента .

Вычислим значение для небазисных компонент.( )

Получили, что все , значит наш план - оптимален.

Проанализируем полученное решение.

1. Распишем полученные перевозки.

Первый пункт потребления получает 100 единиц товара от четвертого производителя.

Второй пункт потребления получает 120 единиц товара от первого производителя.

Третий пункт потребления получает 80 единиц товара от третьего производителя.

Четвертый пункт потребления получает 270 единиц товара от второго производителя и 30 единиц от четвертого производителя.

Пятый пункт потребления получает 150 единиц товара от первого производителя.

2. Определим необходимые объёмы производства.( фактические)

3. Оптимальное значение целевой функции ( минимальная стоимость перевозок) равна 1760 ден.ед.

ЛЕКЦИЯ 10.

Целочисленное линейное программирование.

Постановка задачи ЦЛП. Задача Линейного программирования в постановке

Где , называется задачей целочисленного линейного программирования. Причем, если , то задача частично целочисленная, а если ,то полностью.

Отдельным случаем задач ЦЛП являются задачи ЛП с булевыми переменными. К этом случае дополнительные условия записываются так : , при этом остаются целыми. Это означает, что неизвестные принимают только значения 0 или 1.

Задачи ЦЛП составляют большой класс так называемых нерегулярных задач. Область определения этих задач конечна, но не связанная, не все точки многогранника, который задается системой ограничений, являются допустимым решением. Поэтому для решения этих задач необходимы новые методы решения, отличные от методов ЛП.

Некоторые модели задач цлп.

Задачи с неделимостью. Класс задач с неделимостями представляется двумя типами моделей. Первый тип моделей это обычные целочисленные модели ЛП. Т.е.

К такой модели сводится задача определения оптимальной производственной программы предприятия с индивидуальным или мелкосерийным типом производства. В этом случае означает объем производства объектов, которые обязательно должны быть неделимы.(т.е.измеряться в штуках).

Приведем примеры задач такого типа.

1)Пусть есть m видов транспортных единиц для перевозки груза .Грузоподъемность i-ой транспортной единицы составляет p_i тонн. Груз должен быть доставлен по n направлениям , по b_i тонн каждому. Фонд полезного времени i- ой транспортной единицы - T_i часов. Продолжительность доставки i-ой транспортной в j-ом направлении - t_ij часов, а стоимость этой доставки - c_ij грн. Необходимо определить количество транспортных единиц каждого вида, которые идут вовсе направления. Распределение будем считать оптимальным, если суммарная стоимость доставки всех грузов будет минимальной.

Построим модель. Обозначим через x_ij - количество транспортных средств i– ого вида идущих в j-ом направлении. Тогда

ограничения на фонд времени

ограничения на доставку грузов

ограничения на неизвестные

Условие целочисленности неизвестных обязательна, так как это количество транспортных средств.

2) Задача про ранец. Есть n предметов , заданы величины: a_j-вес предмета j ; c_j - ценность предмета j.Необходимо загрузить ранец, грузоподъемность которого равна А, набором предметов с максимальной суммарной ценностью.

Введем переменные x_j , которые принимают значения

тогда задача про ранец запишется так

В других вариантах этой модели может быть несколько типов ограничений, например, ограничения не только на суммарную массу предметов, но и на суммарный объем и т.д.Такие задачи называются багатомерными задачами про ранец. А если, предположить , что каждый предмет может загружаться не в одном экземпляре, а в нескольких, то ограничения заменятся условием неотрицательности и целочисленности всех неизвестных.

Экстремальные комбинаторные задачи. Комбинаторные экстремальные задачи могут быть решены методом проб и ошибок, т.е. имеют чисто переборный характер, так как варианты решений задач или известны, или легко комбинируются.

1)Пример задачи: задача про назначения. Пусть есть работ n и n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами c_ij . Необходимо найти назначения кандидатов на все работы, которые дают минимальные суммарные затраты; причем каждого кандидата можно назначить только на одну работу и каждая работа может быть занята только одним кандидатом.

Иначе говоря, решение этой задачи представляет собой перестановку (p₁,p₂,…,p_n) , каждое из чисел описывается соответствием .При этом единственность выбора варианта выполняется автоматически и наша цель сводится к минимизации суммы по всем перестановкам .

Это типовая экстремально комбинированная задача. Ее решение путем прямого перебора, т.е. вычисление значении целевой функции при всех перестановках и сравнения их, практически невозможно при больших n, так как число перестановок будет .Известно, что каждая такая перестановка может быть описана точкой в двухмерном евклидовом пространстве. Эту точку удобно представить в виде матрицы . Элементы x_ij этой матрицы можно описать так:

Элементы матрицы Х должны удовлетворять следующим условиям

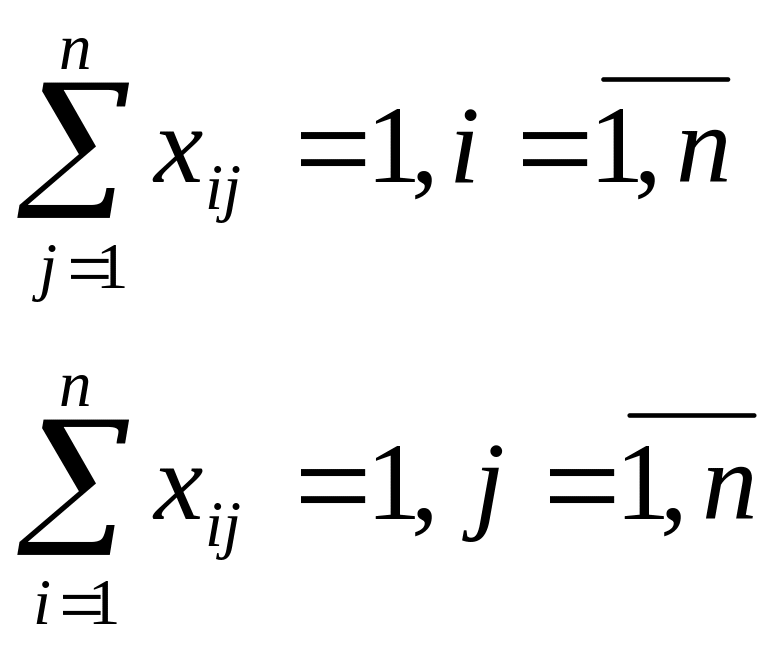
Эти условия говорят, что в каждой строке и в каждом столбце матрицы Х есть только по одной единице. Иначе говоря, каждый кандидат имеет работу и каждая работа имеет своего кандидата. Эти назначения должны быть такими , чтобы минимизировать суммарные затраты, получаем целевую функцию

Условие, что x_ij это булевая переменная можно записать так .

2) Задача про коммивояжера. Пусть n есть городов. Известна матрица расстояний между любой парой городов .Выезжая из начального города, коммивояжер должен побывать во всех городах ровно один раз и вернуться в начальный город. Необходимо узнать в каком порядке нужно объезжать города, чтобы пройденный путь был минимальным.

Введем неизвестные

Тогда получаем задачу

Первая группа ограничений говорит о том , что коммивояжер выезжает из каждого города один раз, а вторые о том, что он один раз въезжает в каждый город.

ЛЕКЦИЯ 11.