Транспортная задача линейного программирования.

Это отдельный вид задачи ЛП. Экономически эта задача формулируется так: Есть пунктов производства, на которых изготавливается однородный продукт в объеме на каждом. Есть также пунктов потребления, которые потребляют эту продукцию. Обьем потребления в каждом пункте единиц. Известна стоимость перевозки единицы продукции из любого пункта производства в любой пункт потребления - Необходимо определить объемы перевозок так, чтобы минимизировать транспортные расходы.

Обозначим через - объём перевозки из -го пункта производства в -ый пункт потребления. Тогда целевая функция будет иметь вид:

(10)

Система ограничений состоит в том ,что вывоз продукции ограничен объемом производства, а доставка объемами потребления. Система ограничений зависит от соотношения суммарного объема производства к суммарному объему потребления. Возможны три случая:

В первом случае вся продукция из пунктов производства вывозится и доставляется потребителям в необходимом объеме. Ограничения записываются в виде равенств, т.е.

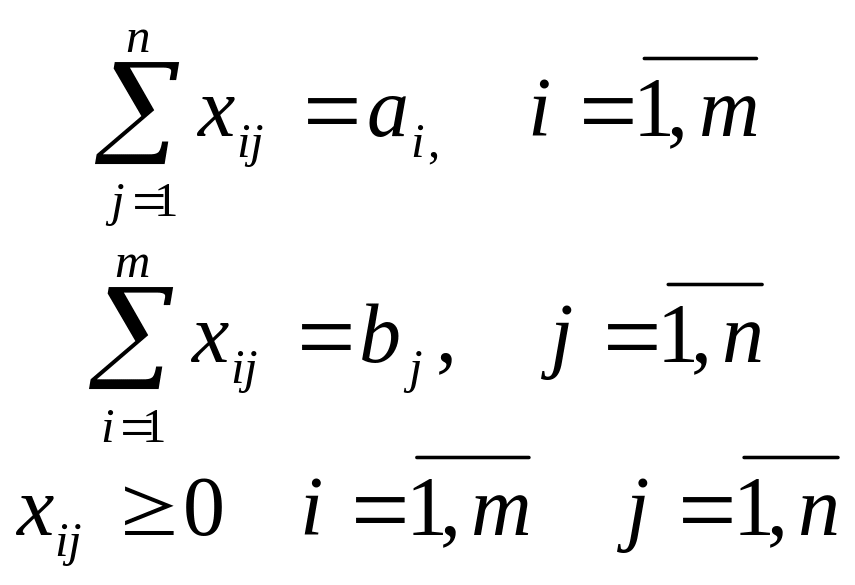(11)

Транспортная задача в постановке 10 – 11 называется сбалансированной задачей, а вид записи – каноническим.

Во втором случае изготавливается продукции больше, чем потребляется. Т.е. ,часть продукции остается не потребленной. Ограничения задачи записываются так:

(12)

ТЗ в постановке 10, 12 называется несбалансированной, случай перепроизводства.

В третьем случае продукции, которая производится недостаточно для удовлетворения спроса. Т.е. не все потребители получат достаточное количество продукции. Ограничения задачи запишутся так:

(13)

ТЗ в постановке 10, 13 называется несбалансированной, случай недопотребления.

Любая несбалансированная задача может быть приведена к сбалансированной. Для случая перепроизводства вводится фиктивный потребитель, который заберет весь остаток не потребленной продукции. А практически это означает, что продукция останется на складах предприятий производителей.

Для случая недопроизводства вводится фиктивный производитель, который условно дает всю не достающую продукцию. А практически это означает, что потребители не дополучили продукцию. Ввод фиктивного потребителя или фиктивного производителя это абсолютно математический прием, который нужен для возможности решения задачи.

Таким образом, если

1) , то вводим фиктивного потребителя

2) , то вводим фиктивного производителя

И так чтобы начать решение транспортной задачи мы должны представить ее в сбалансированном виде ( каноническом виде).

Планом ТЗ будет матрица, в которой соблюдается баланс строк и столбцов.

Начальный опорный план может быть определен разными способами. Наиболее распространенными из них являются метод северо – западного угла и метод наименьшего элемента. Рассмотрим на примере эти два метода.

При использовании метода северо-западного угла заполнения матрицы положительными элементами начинают из компоненты и «перемещаются» по диагонали, направляясь к юго-восточному углу, а именно . Если то ; если то .

Следующим ненулевым элементом будет , или в зависимости от того или стали нулевыми. На к -ом шаге определяем ( при этом a_i  0 и b_j  0); если , то ; если , то . При определении следующего элемента возможен случай, что . Тогда получаем, что и Если это не последний положительный , то получили вырожденный опорный план. Нужно ввести базисный нулевой элемент, иначе условие опорности не выполнится.

При определении опорного плана методом наименьших элементов принимает участие матрица стоимостей, элементы которой направляют. В матрице , выбирается минимальный элемент. Пусть тогда Дальше процедура аналогична предыдущему методу. После образования элемента и пересчета , переходим к выбору следующего минимального элемента, который не должен находится в строке (столбцы), которая удерживает нулевой ai (нулевой bj). Процедура продолжается, пока все ai и bj не станут нулевыми. Если при определении опорного плана был случай вырожденности, то вводим нулевые базисные элементы.

Рассмотрим пример.

Пример:

Задача не сбалансирована. Случай перепроизводства. Вводим фиктивного потребителя. . Получаем сбалансированную задачу.

Построим начальный опорный план методом северо-западного угла:

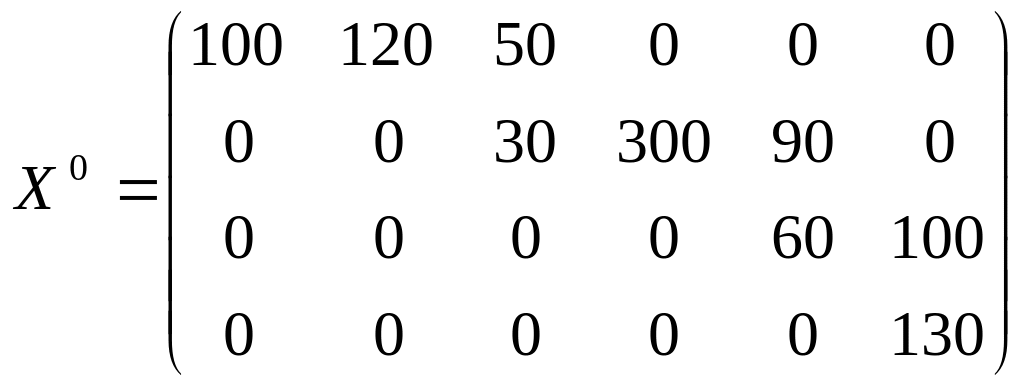
Построим начальный опорный план методом минимального элемента:

Решить транспортную задачу можно используя метод потенциалов .

Вопрос для самоподготовки

1. От чего зависит структура системы ограничений транспортной задачи?

2. Экономическое значение фиктивного потребителя. Как это использовать при определении количеству нужного продукта?

3. Чем отличаются и что общее для методов северо-западного угла и метода наименьших элементов?

ЛЕКЦИЯ 8.