Решение задачи лп с любым видом ограничений. Метод искусственного базиса.

(М-метод).

Если система ограничений представлена неравенствами вида или равенствами, то начальный опорный план не может быть найден так же просто, как в предыдущем методе. В таких случаях начальный опорный план отыскивается с помощью искусственных переменных.

Пример:

Приведем задачу к каноническому виду:

Данная система не решена относительно положительного единичного базиса, введем в нее искусственные переменные х₇ и х₈ , не имеющих никакого отношения к содержательной постановке задачи, но позволяющие получить начальный допустимый базис.

Для исключения из базиса этих переменных, их вводят в целевую функцию с большим отрицательным коэффициентами М . Таким образом из исходной получается новая М – задача.

Выбрав в качестве начального базиса векторы А₅,А₇,А₈, решаем полученную М – задачу с помощью табличного симплекс-метода. Для этого рассчитаем оценки (строку ).

Выразим х₇ и х₈ из ограничений:

Подставим эти выражения в целевую функцию и приведем подобные:

Заполним первую симплекс таблицу:

Баз.перемен.	Решение	А1	А2	А3	А4	А5	А6	А7	А8
Х5	4	2	1	3	-1	1	0	0	0
Х7	3	1	3	1	1	0	0	1	0
Х8	2	1	2	4	2	0	-1	0	1
	-5М	-1-2М	-2-5М	-3-5М	-5-3М	0	М	0	0

Дальнейший расчет как в предыдущем методе. Постепенно из решения задачи уйдут все искусственные переменные.

Двойственность в лп.

Каждой задаче ЛП с любым типом ограничений можно поставить в соответствие другую задачу, которая называется двойственной по отношению к первой. Совместное рассмотрение таких пар задач позволяет исследовать влияние изменения переменных системы на значение целевой функции, проводить экономический анализ результатов расчета.

Правила построения двойственной задачи:

1. Если прямая задача была задачей максимума, то двойственная будет задачей минимума, и на оборот;

2. Число переменных двойственной задачи равно числу ограничений прямой, и наоборот;

3. Коэффициенты целевой функции прямой задачи становятся свободными членами ограничений двойственной задачи;

4. Свободные члены ограничений прямой задачи становятся коэффициентами целевой функции двойственной задачи;

5. Матрица ограничений двойственной задачи получается транспонированием матрицы ограничений прямой, и наоборот;

6. Взаимно однозначное соответствие между переменными исходной задачи и ограничениями двойственной удовлетворяет следующему положению:

А) если J-ая переменная неотрицательна в прямой задаче, то J-ое ограничение в двойственной задаче это неравенство типа ; переменным не имеющих ограничений в знаке соответствует ограничение равенство;

Б) если I-ое ограничение прямой задачи неравенство типа , то

I-ая переменная двойственной задачи неотрицательна; ограничениям равенствам отвечает переменная без ограничений в знаке.

Пример: Построить задачу, двойственную к данной:

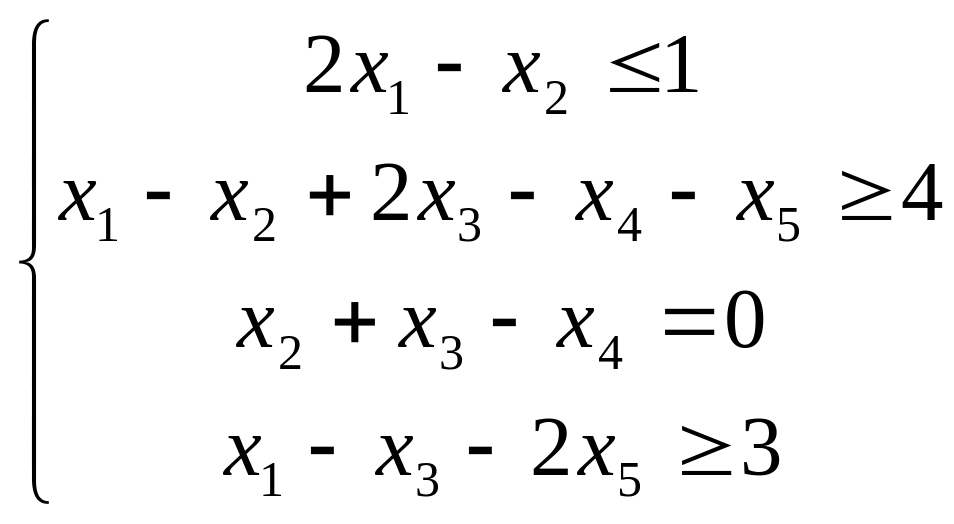
Перепишем задачу изменяя ограничения типа на ограничения типа . Получим задачу:

Двойственная задача имеет вид:

Вопрос для самоподготовки

1. Когда используется метод искусственного базиса при определении опорного плана?

2. Как организуется симплекс-таблица при решении задачи ЛП методом искусственного базиса?

3. Как определяется, что задача не имеет опорных планов?

4. Двойственная задача - это модель прикладной задачи или ее превращения?

5. Как определить количество переменных у двойной задачи, если известна прямая задача?

6. Как определить знаки двойных переменных?

ЛЕКЦИЯ 6.