Міністерство освіти та науки України

ОДЕСЬКІЙ НАЦІОНАЛЬНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ

Кафедра прикладної математики та інформаційних технологій

КОНСПЕКТ ЛЕКЦІЙ

По курсу

«Оптимізаційні моделі та методи їх розв’язку»

для студентів за напрямом навчання 6.030504 –

«Економіка підприємства»

Затверджено на засіданні

кафедри ПМІТ

Протокол № 6 від 16.01.2015 р.

Одеса 2015

Конспект лекцій по курсу „Оптимізаційні моделі та методи їх розв’язку ” для студентів за напрямом 6.030504 -„Економіка підприємства ”/ Укладач: Н.А.Гуляєва. Одеса,ОНПУ,2015.-32 с.

Укладач: Гуляєва Н.А., ст..викладач

Пропонований конспект призначені для студентів економічних спеціальностей. Його мета в доступній та стислій формі ознайомити студентів з основами теорії оптимізаційних моделей та методами розв’язку оптимізаційних задач. Викладений матеріал ілюструється прикладами розв’язання задач. Наведен список рекомендованої літератури.

Призначається для студентів денної форми навчання.

ЗМІСТ

Вступ …………………………………………………………………………………………4

Лекція 1.

1.Поняття оптимізаційної задачі …………………………………………………5

2.Задача математичного програмування. Класи задач МП…………………….. 6

Лекція 2.

1. Задача визначення оптимальної програми підприємства…………………….7

2. Задача розподілу виробничої програми по видам взаємозамінного

Обладнання………………………………………………………………………….8

Лекція 3.

1. Задача лінійного програмування. Канонічний вигляд задачі ЛП …………..9

2. Графічний метод розв’язку задач лінійного програмування……………….11

Лекція 4.

1. Табличний симплекс-метод……………………………………………………..12

2. Приклад розв’язку задачі ЛП симплекс методом……………………………...14

Лекція 5.

1. Розв’язок задач ЛП з любим виглядом обмежень……………………………….15

2. Подвійність в задачах ЛП. Правила побудови подвійних моделей…………….16

Лекція 6.

Економічний аналіз розв’язку задач лінійного програмування…………………….17

Лекція 7.

1. Транспортна задача ЛП. Моделі транспортної задачі………………………………19

2. Методи побудови опорних планів транспортної задачі……………………………..21

Лекція 8.

1. Розв’язок транспортної задачі методом потенціалів………………………………...23

2. Метод потенціалів для задачі з планом побудованим методом південно

західного кута …………………………………………………………………………..24

Лекція 9 .

Метод потенціалів для задачі з планом побудованим методом мінімального

елементу. ………………………………………………………………………………...25

Лекція 10.

Цілочісельне лінійне програмування. Моделі задач ЦЛП. …………………………...27

Лекція 11.

Методи розв’язку задач ЦЛП………………………………………………………….…30

Лекція 12.

Розв’язок задачі комівояжера методом гілок та меж……………………………….….31

Список літератури………………………………………………………………………………...36

Вступ

Курс «Оптимізаційні моделі та методи їх розв’язку» викладається студентам напряму 030504 – «Економіка підприємства», спеціальності 6.030504 – «Економіка підприємства» у четвертому навчальному семестрі. Він узагальнює, закріплює та поглиблює отримані студентами знання після вивчення дисциплін «Економічна теорія», «Вища математика». Робоча навчальна програма з дисципліни передбачає наприкінці семестру складання іспиту.

Даний конспект призначен для підготовки студентів до іспиту з дисципліни «Оптимізаційні моделі та методи їх розв’язку», поглиблення теоретичних та практичних навичок.

ЛЕКЦИЯ 1.

В нашем курсе мы будем рассматривать задачи оптимизации.

Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.

Предметом математического программирования (МП) является класс задач организационного управления с ограничениями в виде равенств и не равенств. Такие задачи вызывают интерес, как у экономистов, так и у математиков и инженеров. Моделирование экономических, технических и технологических процессов, выбор оптимального варианта перевозок, распределение ресурсов, определение производственных и непроизводственных проблем формулируются как задачи математического программирования.

Постановка задачи математического программирования.

МП является основным математическим аппаратом для формализации решения оптимизационных задач. Рассмотрим из чего состоит оптимизационная задача. Есть множество альтернативных решений, возможность количественно оценить каждое решение, сравнить их между собой и выбрать из них лучшее по некоторому критерию. Для того чтобы математически описать такую задачу необходимо ввести понятие варианта, математически описать множество вариантов и оценку варианта.

Пусть вариант представляется в виде вектора Х= (х₁,х₂,…х_n). Множество вариантов получаем путем комбинирования значений х_j ,j=1,n. Но при этом выбор вариантов ограничен некоторыми условиями. Таким образом описать множество вариантов – это ограничить множество значений переменных х_j. Математический язык – это язык функций. Значит, множество возможных значений переменных х_j описывают с помощью функций, например g_i(), значение которых ограничено. Оценка вариантов также будет значением некоторой функции f(x₁,x₂,…,x_n).

Варианты сравниваются между собой на основе оценок. Варианты оценок могут быть различными. Наилучший вариант будет лучшим по отношению к некоторому критерию. Наилучших вариантов в множестве вариантов будет столько сколько стоит критериев сравнения.

Формально задача МП состоит в необходимости определения экстремума некоторой аналитически заданной функции, т.е.

(1)

на некотором подпространстве евклидового пространства, определяемом совокупностью функций

(2)

причем

(3)

Принято называть функцию (1)- целевой функцией, систему функций (2)- системой ограничений, а (3) – дополнительными условиями на неизвестные величины.

Сформулировать задачу МП значит:

• Определить цель

• Задать множество искомых величин

• Записать целевую функцию как функции от искомых величин

• Записать систему ограничений как функции от искомых величин

Решение задачи МП представляется двумя алгебраическими объектами:

• Величиной Z, количественным значением цели

• Совокупностью 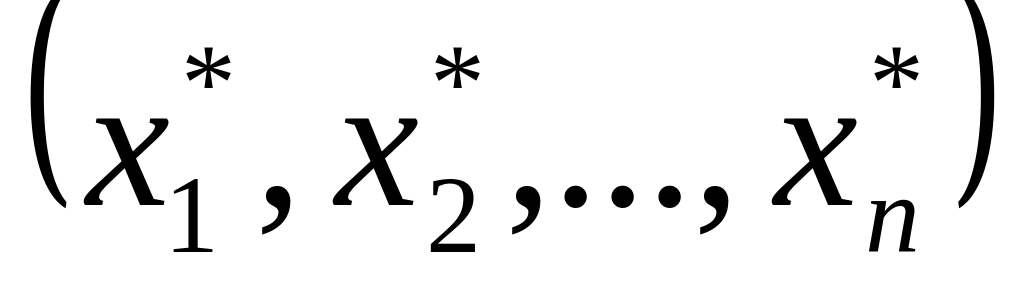- оптимальный вариант

Классы задач мп.

Методы решения задач МП зависят от того, какой вид имеют функции и функции , а также какие условия накладываются на неизвестные. Кроме того когда записываются функции f и g кроме неизвестных в них могут входить и некоторые числовые величины, которые называются составными. Составные могут быть постоянными (детерминированными величинами) или принимать значения из заданного интервала, или принимать случайные значения. Таким образом, выделяют следующие параметры классификации задач МП:

• Вид функций

• Вид множества D

Если функция f и все функции g линейные функции, то задача МП называется задачей линейного программирования (ЛП). Задача называется задачей нелинейного программирования , если функция f или хотя бы одна из функции g будут нелинейными.

Если множество D - это объединение нескольких множеств, то задача МП называется дискретной задачей МП. Если множество D - это множество натуральных чисел, то задача МП называется задачей целочисленного программирования. Задача МП называется задачей непрерывного программирования, если все компоненты неизвестных положительны.

По составляющим задачи МП делятся на два противоположных класса. Если все составляющие заранее заданные величины, то такая задача МП называется детерминированной задачей или задачей детерминированного программирования. Второй класс задач – это задачи стохастического программирования (СХП). В этих задачах в постановке есть случайные величины. Задачи СХП и методы их решения представляют методику принятия решений в условиях неопределенности.

Вопросы для самоподготовки

1. Чем характерна линейная задача?

2. Что является решение задачи ЛП?

3. Что определяет класс линейной задачи?

ЛЕКЦИЯ 2.

Задачи математического программирования.

Задача определения оптимальной производственной программы предприятия. Пусть предприятие выпускает найменований изделий ( ). Для их изготовления используется найменований ресурсов в количестве каждого. Известна норма расхода го ресурса на единицу го изделия - . Задана прибыль от продажи единицы го изделия- . Необходимо составить план производства так, чтобы используя только имеющиеся ресурсы получить максимальную прибыль.

Обозначим через - объем выпуска го изделия. Тогда математическая модель запишется следующим образом:

_{Приведем пример: Изделия N1 и N2 изготовляются на фрезерных станках. Для их изготовления есть 100 кг металла. Затрата металла на изготовление одного изделия N1 составляет 2 кг, а на N2-4кг. Трудоемкость изготовления 100 и 120 станкогодин соответственно для изделий N1 и N2. Мощность фрезерных станков 2000 станкогодин на период, который рассматривается. Составить план производства, которое обеспечивает получение наибольшей выручки от продажи изделий, если отпускная цена одного изделия N1 установлена 3 грн, а изделию N2-2 грн, причем , причем изделий N1 нужно изготовить не больше 40 штук, а изделий N2-не больше 20 штук.}

_{Построим модель данной задачи: Обозначим через х1- объем выпуска изделия №1, а через х2 –объем выпуска изделия №2. Тогда модель имеет вид:}

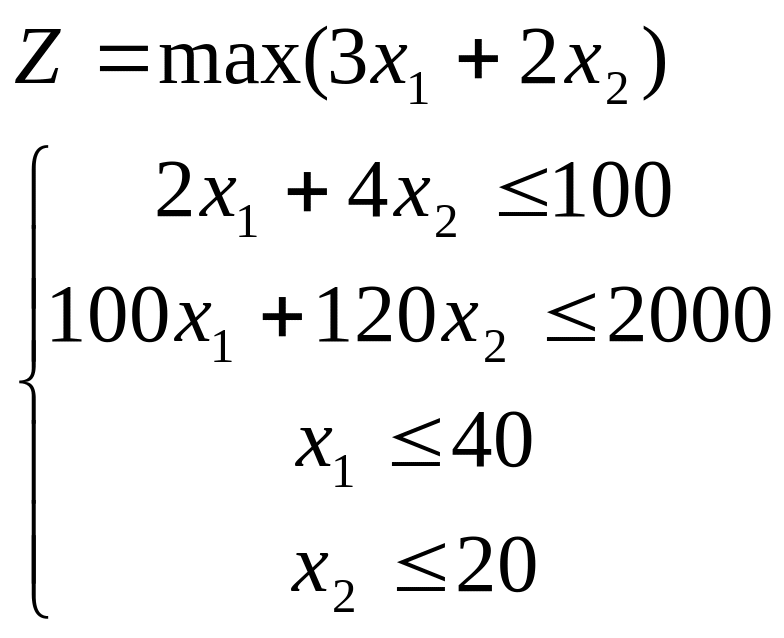
Задача распределения изделий по видам взаимозаменяемого оборудования:

Пусть предприятие выпускает найменований изделий . В объеме ( ) каждого. Для их изготовления используется видов взаимозаменяемого оборудования. Известен фонд полезного времени для каждого типа оборудования . Трудоемкость и себестоимость изготовления изделия зависит от типа оборудования . не обходимо выполнить план предприятия с минимальной суммарной себестоимостью.

Обозначим через - объем выпуска -го изделия на ом оборудовании.

Тогда модель задачи имеет вид:

_{Приведем пример:}

	/
	1	2	3	4	5	6
1	25/8	12/4	16/5	23/8	14/7	23/8	2100
2	15/7	17/6	-	16/6	19/8	17/6	1400
3	13/4	14/5	24/8	14/5	-	15/5	1800
4	10/3	13/6	12/4	25/8	16/7	10/4	2000
5	24/8	12/6	-	19/6	16/8	13/5	2040
bj	240	180	260	170	160	200

Обозначим через - объем выпуска -го изделия на -ом типе оборудования. Тогда модель имеет вид:

( ; )

Решив эту задачу получим следующее решение.

остальные

Проанализируем решение:

1. Распределение изделий по видам оборудования:

На 1-ом типе оборудования изготавливаются изделия 2- го типа в объеме 180 ед и изделия 5 типа в объеме 160 ед.( )

На 2 –ом типе оборудования изделия не изготавливаются.

На 3-ем типе оборудования изготавливаются изделия 4- го типа в объеме 170 ед ( )

На 4-ом типе оборудования изготавливаются изделия 1- го типа в объеме 240 ед, изделия 3 типа в объеме 260 ед., изделия 6-го типа в объеме 60 ед.( ).

На 5-ом типе оборудования изготавливаются изделия 6- го типа в объеме 140 ед ( ).

2. Коэффициент загрузки оборудования, вычисляется по формуле:

3. Оптимальный парк оборудования, вычисляется по формуле:

; ; ; ;

4) Оптимальная себестоимость. Вычисляется как значение целевой функции.

Вопросы для самоподготовки

1. Что определяется в задаче определение оптимальной производственной программы?

2. Что определяет целевая функция в задаче определения оптимальной производственной программы?

3. Что определяет ограничение в задаче определения оптимальной производственной программы?

4. Запишите математическую модель задачи определения оптимальной производственной программы?

5. Что определяется в задаче распределения производственной программы по видам оборудования ?

6. Как определить оптимальный парк оборудования для выполнения производственной программы?

7. Запишите математическую модель распределения производственной программы по видам оборудования ?

ЛЕКЦИЯ 3.

Линейное программирование.

Формально задача ЛП записывается так:

(4)

при ограничениях

(5)

(6)

где

Задача, в которой нужно найти максимум функции (4) при условиях (5), приведенных к равенствам, и условиях (6), называется задачей ЛП в канонической форме.

Канонический вид записи:

(7)

при ограничениях

(8)

(9)

Для задач в канонической форме созданы методы решения. Любая форма записи ЛП задач может быть приведена к каноническому виду путем алгебраических преобразований.

Если целевая функция есть функцией минимизации, то привести ее к виду (7) можно заменой знаков составляющих . Т.е.

Если ограничения имеют знак , то привести к равенству можно путем введения дополнительных переменных со знаком «+». Т.е.

Если ограничения имеют знак , то привести к равенству можно путем введения дополнительных переменных со знаком «-». Т.е.

В системе ограничений могут быть неравенства с разными знаками, а так же равенства. Алгебраические преобразования проводят только для неравенств.

Пример:

Приведем задачу к каноническому виду:

Вектор , удовлетворяющий ограничениям задачи ЛП (5), называется ее решением либо планом. Если переменные удовлетворяют еще и условиям неотрицательности (6), то Х называется допустимым планом или допустимым решением. Множество R(X) допустимых планов, представляет собой область допустимых решений (ОДР) задачи ЛП, является выпуклым многогранным множеством.

Допустимый план, соответствующий крайней точке множества, является опорным планом или допустимым базисным решением задачи ЛП. Опорный план, обращающий в максимум или минимум целевую функцию, называется оптимальным планом задачи ЛП.