4.2 Расчет элементов конструкций на сдвиг

При чистом сдвиге в поперечном сечении стержня действует только перерезывающая сила Q и соответственно только каса­тельные напряжения.

В сплошном материале деформацию сдвига можно осущест­вить, например, если подвергнуть кручению тонкостенную трубу. Прямоугольные до деформации элементы материала стенок трубы превращаются в параллелограммы за счет изменения первоначаль­ного прямого угла на малый угол g , называемый углом сдвига.

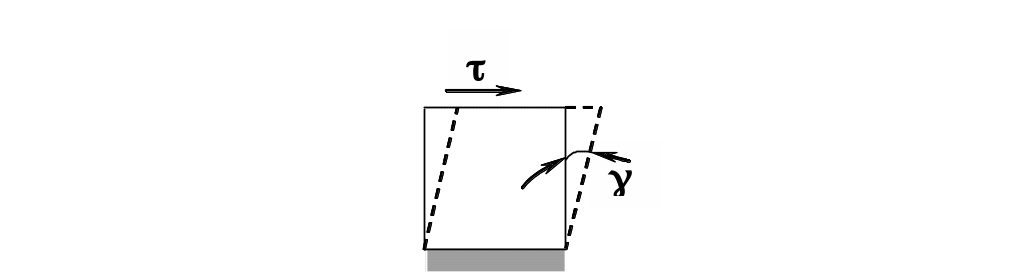
Рисунок 4.4

При сдвиге, на взаимно перпендикулярных площадках каса­тельные напряжения численно равны и направлены так, что стре­мятся вращать элемент в противоположные стороны (закон парно­сти касательных напряжений).

Площадка сдвига образует с главной площадкой угол равный 45 градусов. По площадке сдвига не действуют нормальные напря­жения, поэтому она называется площадкой чистого сдвига.

Экспериментальные зависимости чистого сдвига обычно проводят путем кручения трубчатых образцов, получая зависи­мость между напряжением ( t ) и углом сдвига ( g).

Рисунок 4.5

До предела пропорциональности t_пц справедлив закон Гука:

t = G g

где, G – модуль сдвига; g - угол сдвига.

Смещение γ называют абсолютным сдвигом или углом сдвига. Деформации сдвига могут определяться по формуле:

g = t / G не только при чистом сдвиге, но и в общем случае плос­кого напряженного состояния – когда по боковым граням паралле­лепипеда действуют не только касательные, но и нормальные на­пряжения, которые вызывают лишь поступательные перемещения боковых граней параллелепипеда и не вызывают изменения его прямых углов.

Из уравнения потенциальной энергии при сдвиге устанавли­вается связь между тремя константами изотропного материала:

G = ,

где, Е – модуль упругости при растяжении (1-го рода);

m - коэффициент Пуассона;

G – модуль сдвига (2-го рода).

В некоторых конструкциях по отдельным сечениям дейст­вуют значительные касательные напряжения, а нормальные отно­сительно малы. Поэтому в приближенных расчетах учитываются лишь касательные напряжения, а указанные сечения рассматрива­ются как площадки чистого сдвига. Такие расчеты называются рас­четами на сдвиг, или на срез, или на скалывание. Например, закле­почные, болтовые и сварные соединения.

Разрушение заклепочного соединения может произойти в ре­зультате среза заклепок по плоскости ab, среза (выкалывания) лис­тов за крайними заклепками (по плоскости cd) или между заклеп­ками. Также смятия по диаметральной плоскости заклепки (abcf) и разрыва листа.

Рисунок 4.6

Расчет может быть проектировочный, проверочный и нагру­зочный. Для расчета используют условия прочности на срез:

t_cp = [t];

на смятие:

s_cм = [s_cм];

на разрыв листов:

s_p = [s_p], A_p = bt - n¢dt,

где, Q – поперечная сила; А – площадь среза, смятия закле­пок и разрыва листов; Р – усилие; d – диаметр заклепки; t – тол­щина листов; n – общее число заклепок; b – ширина листов, n′ - число заклепок в опасном сечении.

Расчет болтового соединения, с установкой болтов в отвер­стие без зазора, аналогичен заклепочному. Дополнением будет рас­чет болтов на растяжение вдоль их продольной оси:

s_p = [s_p].

Для того чтобы не производить расчет на срез (выкалывание) листов за крайними заклепками или болтами или между ними, рас­пределяют заклепки (болты) в плане соединения так, чтобы мини­мальное расстояние от центра крайнего отверстия до края прикреп­ляемого элемента (листа) по направлению действия силы равнялось 2d. Минимальное расстояние между осями отверстий – 3,5 d.

Допускаемые напряжения на срез при статической нагрузке принимают:

- для пластичных материалов [t_cp] = (0,6 0,8)[s_p];

- для хрупких материалов [t_cp] = (0,8 1,1)[s_p].

Допускаемое напряжение на смятие принимают равным:

[s_см] = (2,0 2,5)[s_p].

Расчет стыковых сварных швов ведут на растяжение (сжа­тие) по условию прочности:

s_св = [s_св].

Расчетную ширину шва берут на 2k меньше ширины де­тали, где k = 5 мм – не провар в начале и конце шва. Высоту шва принимают обычно равной толщине d детали.

При соединении листов внахлест, расчет фланговых и лобо­вых швов ведут на срез по бессекторному сечению, пренебрегая из­гибом шва. Считая шов равнобедренным прямоугольным треуголь­ником, получим высоту шва

h = d cos 45^o 0,7 d.

Тогда условие прочности будет иметь вид:

t_св = [t_св],

где, - расчетная длина шва. Полная длина шва удлинится на 2k (k = 5 мм – не провар): = .

Допускаемые напряжения устанавливаются в зависимости от материала свариваемых деталей, вида нагрузки и условий работы, типа электродов и способа сварки. Например: для ст.3 – на растя­жение [s_св]_р 100 мПа, на сжатие [s_св]_сж 110 мПа и на срез [t_св]_cp 80 мПа.

Длину фланговых швов не рекомендуется принимать более 25 толщин свариваемого металла.