Самостоятельная работа №4
Вариант 1
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-5 |
-2 |
1 |
8 |
10 |
18 |
13 |
7 |
10 |
9 |
Для построения эмпирической функции распределения необходимо найти относительные частоты и накопленные относительные частоты.
Относительные
частоты могут быть найдены как
,
где N
– объем выборки,
.
Накопленные
частоты находятся из соотношения
xi |
-5 |
-2 |
1 |
8 |
10 |
ni |
18 |
13 |
7 |
10 |
9 |
wi |
18/57 |
13/57 |
7/57 |
10/57 |
9/57 |
Wi |
18/57 |
31/57 |
38/57 |
48/57 |
57/57 |
Теперь
можно построить эмпирическую функцию
распределения, которая представляет
собой частоту события X<x:
.
Выборочное
среднее может быть найдено по формуле
.
Выборочная
дисперсия определяется как
.
Однако, применение данной формулы
сопряжено с расчетами, как правило
содержащими дроби, появляющиеся после
вычисления среднего значения. Это
обстоятельство только усугубляется
возведением в квадрат. Поэтому, при
нахождении выборочной дисперсии, как
правило, пользуются не определением, а
расчетной формулой
.
Для ее применения найдем сперва среднее
значение x2:
.
Выборочное
среднеквадратическое отклонение может
быть найдено как корень из выборочной
дисперсии:
.
Известно,
что выборочная дисперсия является
смещенной оценкой дисперсии генеральной
совокупности. Для получения несмещенной
оценки пользуются исправленной дисперсией
.
Аналогично
вводится понятие «исправленного»
среднеквадратического отклонения
.
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
Построение
доверительного интервала сводится к
нахождению таких значений x1
и
x2
для
неизвестного параметра X,
что
,
где
– доверительная вероятность (надежность
доверительного интервала). Зачастую
доверительный интервал является
симметричным относительно точечной
оценки неизвестного параметра. В этом
случае границы интервала могут быть
определены как
,
а задача построения доверительного
интервала сводится к определению x*
и
.
Рассмотрим несколько наиболее часто встречающихся случаев построения доверительных интервалов.
а)
Построение доверительного интервала
для неизвестного математического
ожидания при известном среднеквадратическом
отклонении. В этом случае в качестве
точечной оценки выступает выборочное
среднее
,
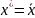а размах доверительного интервала
определяется из соотношения
.
t
– коэффициент, определяемый из соотношения
.
Ф(t)
– интегральная функция Лапласа, её
значения (а, соответственно и значения
обратной функции) могут быть найдены
из приложения 1.
Для
нашей задачи найдем сперва t:
,
1,96.
Теперь
используя данные задачи 1 можно найти
.
Учитывая, что точечная оценка
,
получаем
или
.
б)
Построение доверительного интервала
для неизвестного математического
ожидания при неизвестном среднеквадратическом
отклонении. Вид определяющего соотношения
принципиально не изменяется, однако,
во-первых, поскольку среднеквадратическое
отклонение неизвестно, по в его качестве
выступает точечная оценка – «исправленное»
среднеквадратическое отклонение,
во-вторых, коэффициент определяется не
из таблицы интегральной функции Лапласа,
а из таблицы коэффициентов Стьюдента
(приложение 2). Тогда определяющие
соотношения можно записать как
и
.
Для
нашей задачи
(точного значения в таблице нет, берем
промежуточное, воспользовавшись линейной
интерполяцией
).
Теперь
используя данные задачи 1 можно найти
.
Учитывая, что точечная оценка
,
получаем
или
.
Видим, что доверительный интервал шире,
чем при известном среднеквадратическом
отклонении, поскольку добавляется еще
и его неопределенность.
в)
Построение доверительного интервала
для неизвестного среднеквадратического
отклонения. В этом случае точечной
оценкой выступает «исправленное»
среднеквадратическое отклонение, размах
доверительного интервала может быть
найден из соотношения
,
где q
определяется на основе приложения 3
.
Для
нашей задачи
(точного значения в таблице нет, берем
промежуточное, воспользовавшись линейной
интерполяцией
).
Теперь
используя данные задачи 1 можно найти
.
Учитывая, что точечная оценка
,
получаем
или
.
В случае, если левая граница окажется
меньше 0 (а такое возможно, если q>1),
то оно принимается равной 0, поскольку
среднеквадратическое отклонение не
может быть отрицательным.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 21 раз.
Построение доверительного интервала для неизвестной вероятности наступления события на основе относительной частоты ведется по следующей формуле:
.
t – коэффициент, определяемый из соотношения . Ф(t) – интегральная функция Лапласа, её значения (а, соответственно и значения обратной функции) могут быть найдены из приложения 1.
Для
нашей задачи
,
2,57.
.
Откуда
.
4. Задана выборка.
892,39 |
892,45 |
892,48 |
892,51 |
892,54 |
10 |
18 |
17 |
12 |
13 |
Найти коэффициент асимметрии и эксцесс.
Теоретический
и выборочный коэффициент асимметрии и
эксцесс выражаются через соответствующие
центральные моменты третьего и четвертого
порядка через соотношения
и
.
Начальный
эмпирический момент k-го
порядка случайной величины X
определяется как
.
Центральный
эмпирический момент k-го
порядка случайной величины X
определяется как
.
При этом центральные моменты, как правило, по определению не считаются, а используются расчетные формулы, которые проще в применении. Вид этих формул совпадают для теоретических и эмпирических моментов, разница в том, что для расчета эмпирических центральных моментов в них подставляются эмпирические начальные моменты, а для расчета теоретических – соответственно, теоретические.
;
;
.
Кроме
того, на практике часто встречаются
случаи, когда получаемые в выборке
значение незначительно разбросаны
относительно большой величины (например,
измеряя атмосферное давление мы будем
получать разброс в несколько десятков
миллиметров ртутного столба относительно
сравнительно большой величины нормального
атмосферного давления в 760 миллиметров
ртутного столба. В таких случаях даже
применение расчетных формул не всегда
удобно, поскольку приходится считать
степени значительных величин, получая
значения более миллиарда, тогда как
результат может измеряться десятыми
долями. В таких случаях легко как
ошибиться при расчете, так и получить
ошибку при применении средств
вычислительной техники из-за недостаточного
количества разрядов. В таких случаях
на помощь приходит метод условных
вариант. Он заключается в переходе от
имеющихся в выборке вариант x
к условным x*
путем линейного преобразования
.
При этом коэффициенты a
и b
могут быть любыми, однако для удобства
расчета их выбирают из следующих
соображений: в качестве коэффициента
b
удобно взять одну из вариант, находящихся
посередине выборки. В этом случае
остальные значения будут симметрично
распределены относительно нее и суммарные
значения для нечетных степеней будут
не очень большими. Коэффициент a
берется как наибольший общий делитель
шагов между вариантами. Если шаги
дробные, то их сперва домножают на
знаменатель для приведения к целым, а
после нахождения наибольшего общего
делителя его снова делят на этот
знаменатель.
Поясним на примере нашей выборки. В качестве b возьмем среднюю варианту b=892,48. Шаги между вариантами равны 0,06 0,03 0,03 0,03. Видим, что значения дробные, знаменатель 100. Домножим и получим ряд 6 3 3 3. Наибольший общий делитель этих чисел равен 3. Делим 3 на знаменатель 100 и получаем a=0,03.
Теперь
можем найти условные варианты из
соотношения
и переписать выборку.
X* |
-3 |
-1 |
0 |
1 |
2 |
ni |
10 |
18 |
17 |
12 |
13 |
Очевидно, что после такого преобразования все значения моментов у нас изменятся и после нахождения моментов для условных вариант нужно буден переходить к начальным значениям. Сделать это можно через следующие соотношения:
;
;
;
.
Коэффициент асимметрии и эксцесс от линейного преобразования не изменяются, поскольку содержат домножающий коэффициент в числителе и знаменателе с одинаковой степенью (в числителе – от соответствующего центрального момента, в знаменателе от среднеквадратического отклонения в соответствующей степени, являющегося корнем из второго центрального момента).
Начальные моменты высших порядков сами по себе смысла не несут и используются для получения центральных моментов, поэтому для них в формулах для обратного преобразования необходимости нет.
Для расчета найдем произведения частот и условных вариант в степени до четвертой (поскольку нам нужен максимум четвертый момент для получения эксцесса).
x |
n |
x* |
nx* |
nx*2 |
nx*3 |
nx*4 |
892,39 |
10 |
-3 |
-30 |
90 |
-270 |
810 |
892,45 |
18 |
-1 |
-18 |
18 |
-18 |
18 |
892,48 |
17 |
0 |
0 |
0 |
0 |
0 |
892,51 |
12 |
1 |
12 |
12 |
12 |
12 |
892,54 |
13 |
2 |
26 |
52 |
104 |
208 |
∑ |
70 |
|
-10 |
172 |
-172 |
1048 |
Теперь можем найти начальные моменты для условных вариант:
;
;
;
.
Найдем соответствующие центральные моменты для условных вариант:
;
;
.
Найдем среднеквадратическое отклонение для условных вариант как корень из дисперсии или, по сути, второго центрального момента, который уже рассчитан:
.
Так как нам нужно найти коэффициент асимметрии и эксцесс, то для этих величин обратное преобразование делать не требуется, получим:
;
.
Вариант 2
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-6 |
0 |
4 |
10 |
9 |
8 |
6 |
12 |
9 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 22 раза.
4. Задана выборка.
374,75 |
374,85 |
374,9 |
374,95 |
375 |
13 |
9 |
9 |
2 |
16 |
Найти коэффициент асимметрии и эксцесс.
Вариант 3
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-8 |
-6 |
0 |
4 |
6 |
2 |
14 |
15 |
3 |
5 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 23 раза.
4. Задана выборка.
506,42 |
506,54 |
506,6 |
506,66 |
506,72 |
8 |
18 |
20 |
19 |
17 |
Найти коэффициент асимметрии и эксцесс.
Вариант 4
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-8 |
-3 |
-1 |
4 |
6 |
5 |
13 |
1 |
20 |
10 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 24 раза.
4. Задана выборка.
791,86 |
791,94 |
791,98 |
792,02 |
792,06 |
20 |
19 |
5 |
2 |
9 |
Найти коэффициент асимметрии и эксцесс.
Вариант 5
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-4 |
0 |
1 |
5 |
10 |
2 |
2 |
11 |
4 |
19 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 25 раз.
4. Задана выборка.
955,03 |
955,19 |
955,27 |
955,35 |
955,43 |
12 |
19 |
5 |
11 |
8 |
Найти коэффициент асимметрии и эксцесс.
Вариант 6
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-9 |
-2 |
1 |
4 |
6 |
19 |
14 |
8 |
19 |
5 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 26 раз.
4. Задана выборка.
2608,8 |
2609,2 |
2609,4 |
2609,6 |
2609,8 |
2 |
17 |
15 |
12 |
13 |
Найти коэффициент асимметрии и эксцесс.
Вариант 7
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-6 |
5 |
6 |
7 |
10 |
19 |
14 |
20 |
18 |
2 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 27 раз.
4. Задана выборка.
6594,9 |
6596,5 |
6597,3 |
6598,1 |
6598,9 |
13 |
8 |
13 |
5 |
13 |
Найти коэффициент асимметрии и эксцесс.
Вариант 8
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-1 |
1 |
4 |
5 |
8 |
7 |
6 |
15 |
9 |
20 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 28 раз.
4. Задана выборка.
9891,6 |
9892,4 |
9892,8 |
9893,2 |
9893,6 |
14 |
14 |
8 |
8 |
7 |
Найти коэффициент асимметрии и эксцесс.
Вариант 9
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-7 |
-3 |
7 |
10 |
6 |
7 |
20 |
20 |
16 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 29 раз.
4. Задана выборка.
800,84 |
800,98 |
801,05 |
801,12 |
801,19 |
16 |
7 |
3 |
20 |
1 |
Найти коэффициент асимметрии и эксцесс.
Вариант 10
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-7 |
-6 |
-3 |
-2 |
14 |
3 |
5 |
17 |
9 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 30 раз.
4. Задана выборка.
531,92 |
532,02 |
532,07 |
532,12 |
532,17 |
16 |
14 |
3 |
7 |
13 |
Найти коэффициент асимметрии и эксцесс.
Вариант 11
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-9 |
-3 |
0 |
1 |
9 |
6 |
19 |
19 |
16 |
1 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 31 раз.
4. Задана выборка.
663,22 |
663,38 |
663,46 |
663,54 |
663,62 |
14 |
19 |
10 |
11 |
19 |
Найти коэффициент асимметрии и эксцесс.
Вариант 12
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-9 |
2 |
8 |
10 |
20 |
2 |
5 |
1 |
18 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 32 раза.
4. Задана выборка.
6333,8 |
6335,6 |
6336,5 |
6337,4 |
6338,3 |
16 |
17 |
18 |
2 |
3 |
Найти коэффициент асимметрии и эксцесс.
Вариант 13
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-8 |
-3 |
6 |
8 |
11 |
15 |
3 |
15 |
4 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 33 раза.
4. Задана выборка.
305,57 |
305,65 |
305,69 |
305,73 |
305,77 |
3 |
14 |
15 |
2 |
20 |
Найти коэффициент асимметрии и эксцесс.
Вариант 14
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-8 |
-5 |
6 |
10 |
14 |
12 |
11 |
15 |
6 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 34 раза.
4. Задана выборка.
2186 |
2186,4 |
2186,6 |
2186,8 |
2187 |
11 |
4 |
14 |
15 |
4 |
Найти коэффициент асимметрии и эксцесс.
Вариант 15
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-9 |
-7 |
-5 |
-2 |
7 |
4 |
5 |
5 |
10 |
3 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 35 раз.
4. Задана выборка.
7481,3 |
7482,9 |
7483,7 |
7484,5 |
7485,3 |
12 |
11 |
10 |
5 |
5 |
Найти коэффициент асимметрии и эксцесс.
Вариант 16
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-8 |
-5 |
-4 |
0 |
3 |
10 |
13 |
11 |
4 |
19 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 36 раз.
4. Задана выборка.
4827,5 |
4829,3 |
4830,2 |
4831,1 |
4832 |
9 |
10 |
7 |
15 |
5 |
Найти коэффициент асимметрии и эксцесс.
Вариант 17
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-7 |
-6 |
-2 |
0 |
1 |
3 |
8 |
2 |
1 |
1 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 37 раз.
4. Задана выборка.
250 |
250,16 |
250,24 |
250,32 |
250,4 |
20 |
16 |
3 |
17 |
5 |
Найти коэффициент асимметрии и эксцесс.
Вариант 18
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-6 |
-5 |
2 |
4 |
7 |
16 |
8 |
2 |
10 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 38 раз.
4. Задана выборка.
341,95 |
342,05 |
342,1 |
342,15 |
342,2 |
2 |
12 |
18 |
5 |
9 |
Найти коэффициент асимметрии и эксцесс.
Вариант 19
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-4 |
-3 |
-2 |
0 |
4 |
14 |
9 |
18 |
11 |
10 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 39 раз.
4. Задана выборка.
835,86 |
835,92 |
835,95 |
835,98 |
836,01 |
9 |
10 |
7 |
14 |
10 |
Найти коэффициент асимметрии и эксцесс.
Вариант 20
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-5 |
-3 |
-2 |
8 |
10 |
19 |
14 |
10 |
5 |
5 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 40 раз.
4. Задана выборка.
1831,4 |
1831,8 |
1832 |
1832,2 |
1832,4 |
8 |
6 |
4 |
20 |
1 |
Найти коэффициент асимметрии и эксцесс.
Вариант 21
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-6 |
-2 |
0 |
4 |
9 |
3 |
7 |
6 |
10 |
5 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 41 раз.
4. Задана выборка.
4215,2 |
4216,4 |
4217 |
4217,6 |
4218,2 |
9 |
13 |
7 |
7 |
16 |
Найти коэффициент асимметрии и эксцесс.
Вариант 22
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-7 |
2 |
3 |
7 |
9 |
17 |
1 |
11 |
15 |
16 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 42 раза.
4. Задана выборка.
2114,4 |
2114,8 |
2115 |
2115,2 |
2115,4 |
10 |
10 |
13 |
16 |
16 |
Найти коэффициент асимметрии и эксцесс.
Вариант 23
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-1 |
0 |
1 |
6 |
8 |
16 |
9 |
9 |
15 |
8 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 43 раза.
4. Задана выборка.
2680,4 |
2680,8 |
2681 |
2681,2 |
2681,4 |
11 |
12 |
9 |
7 |
16 |
Найти коэффициент асимметрии и эксцесс.
Вариант 24
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-6 |
-3 |
3 |
8 |
10 |
16 |
9 |
13 |
15 |
20 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 44 раза.
4. Задана выборка.
249,11 |
249,17 |
249,2 |
249,23 |
249,26 |
20 |
5 |
6 |
15 |
15 |
Найти коэффициент асимметрии и эксцесс.
Вариант 25
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-10 |
-9 |
-4 |
-2 |
10 |
8 |
11 |
3 |
6 |
13 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 45 раз.
4. Задана выборка.
114,98 |
115,02 |
115,04 |
115,06 |
115,08 |
4 |
9 |
16 |
20 |
2 |
Найти коэффициент асимметрии и эксцесс.
Вариант 26
Самостоятельная работа 4 по теории вероятностей и математической статистике
1. По данному распределению выборки найти эмпирическую функцию распределения, выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, выборочное среднеквадратичное отклонение, исправленное" выборочное среднеквадратичное отклонение:
-6 |
-4 |
-1 |
6 |
10 |
10 |
20 |
10 |
7 |
3 |
2. На основе выборки из задания 1 построить доверительные интервалы для математического ожидания для случая а) среднеквадратическое отклонение генеральной совокупности известно и равно «исправленному» среднеквадратическому отклонению, б) среднеквадратическое отклонение генеральной совокупности неизвестно. в) Также построить доверительный интервал для среднеквадратичного отклонения. Доверительную вероятность во всех расчетах принять равной 0,95.
3. Построить доверительный интервал с надежностью 0,99 для оценки неизвестной вероятности наступления события, если в 100 наблюдениях событие наступило 46 раз.
4. Задана выборка.
472,01 |
472,09 |
472,13 |
472,17 |
472,21 |
9 |
18 |
2 |
12 |
4 |
Найти коэффициент асимметрии и эксцесс.