
Задания в5: вычисление площади плоской фигуры
 Площадь треугольника,
четырехугольника, B
Площадь треугольника,
четырехугольника, B
круга и его частей может быть найдена по формуле, Теорема
выражая длины сторон, высот целым числом делений c a Пифагора:
клетки или для их вычисления использовать теорему c² = a² + b².
Пифагора. A C




 b
b
a а в h h
в а а а а
S = ½ ав S = а² S = ав S = аh S = ½ аh

 в
в
 r
г α
r
г α
S = πr²
S =
![]() h
h
а
S = ½ ( а+ в) h Пример 1.
В5. Найдите площадь квадрата, изображенного на клетчатой
б метрах. Решение: А а Площадь квадрата S = а², где а – его сторона. Из прямоугольного треугольника, например, ВЕС со сторонами 4 см и 2 см С по теореме Пифагора получим: а² = 4² + 2²; а² = 16+4; а² = 20. Тогда S = а² = 20см². D В бланк ответов: В5
2
0
|
Пример 2.
В Размер каждой клетки 1см х 1см .Ответ дайте в квадратных сантиметрах. С Решение: Из прямоугольного треугольника ABE со сторонами 1см и 2см и прямоугольного треугольника AFD со сторонами В D 2см и 4см по теореме Пифагора найдем стороны прямоугольника. Тогда S =АВ·АD,
1
0
|
вычисление площади, примеры 1-4
Содержание
В предложенной задаче данный треугольник является частью квадрата.
В5. Найдите площадь треугольника АВС. Размер каждой
к
К
П лощадь данного треугольника ABC равна разности площади квадрата AKLM и площадей
т
B LC. Используя формулы площади квадрата и А M п рямоугольного треугольника, получим:
S
7
,
5
|
Пример 3.
В задачах на вычисление площади
треугольника или четырехугольника
искомая фигура Ф![]() является частью другой фигуры Ф, которая
разбивается на несколько фигур Ф
является частью другой фигуры Ф, которая
разбивается на несколько фигур Ф![]() .
Для нахождения площади искомой фигуры
Ф
нужно
из площади фигуры Ф вычесть площади
фигур Ф
.
.
Для нахождения площади искомой фигуры
Ф
нужно
из площади фигуры Ф вычесть площади
фигур Ф
.
Это более простой способ решения таких задач, применяя только формулы площади прямоугольника и прямоугольного треугольника.

 умаге
со стороной 1 см. Ответ дайте в
квадратных санти- В E
умаге
со стороной 1 см. Ответ дайте в
квадратных санти- В E
 5.
Найдите площадь прямоугольника АВС
D.
5.
Найдите площадь прямоугольника АВС
D.


 летки
1см х 1 см. Ответ дайте в квадратных
сантиметрах.
летки
1см х 1 см. Ответ дайте в квадратных
сантиметрах. Решение:
Решение: 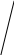
 вадрат
AKLM со стороной 4
см разбит на К В L
вадрат
AKLM со стороной 4
см разбит на К В L
 4
треугольника, один из
которых данный.
4
треугольника, один из
которых данный.

 рех
прямоугольных треугольников
AKB, AMC,
С
рех
прямоугольных треугольников
AKB, AMC,
С