
- •П.В. Столбов Математика
- •Часть II
- •§ 1. Функция двух переменных
- •1. Основные понятия
- •2. Предел и непрерывность функции двух переменных
- •3. Частные производные и дифференцируемость функции двух переменных
- •4. Дифференцирование сложных функций
- •5. Дифференцирование неявных функций
- •6. Касательная плоскость и нормаль к поверхности
- •7. Полный дифференциал функции двух переменных и его геометрический смысл
- •8. Производная по направлению. Градиент
- •Свойства градиента
- •§ 2. Экстремумы функции двух переменных
- •1. Частные производные высших порядков. Экстремумы функции двух переменных
- •2. Наибольшее и наименьшее значение функции в замкнутой области
- •Алгоритм нахождения наибольшего и наименьшего значений дифференцируемой в области функции :
- •§ 3. Первообразная и неопределенный интеграл. Основные приемы интегрирования
- •1. Основные понятия
- •Интегрирование подстановкой.
- •Интегрирование по частям.
- •§ 4. Определенный интеграл
- •1. Задачи, приводящие к понятию определенного интеграла
- •2. Площадь криволинейной трапеции
- •3. Масса линейного неоднородного стержня
- •4. Работа переменной силы на прямолинейном участке пути
- •5. Свойства определенного интеграла
- •6. Вычисление определенного интеграла. Формула Ньютона-Лейбница
- •7. Вычисление определенного интеграла подстановкой
- •8. Вычисление определенного интеграла интегрированием по частям
- •9. Вычисление площади плоской фигуры
- •Контрольные задания
- •Задание 8.
- •Литература
- •Содержание
- •§ 1. Функция двух переменных 3
- •§ 2. Экстремумы функции двух переменных 18
- •§ 3. Первообразная и неопределенный интеграл. Основные приемы интегрирования 29
- •§ 4. Определенный интеграл 36
- •Математика
- •Часть II
- •603950, Н.Новгород, Ильинская, 65
§ 3. Первообразная и неопределенный интеграл. Основные приемы интегрирования
1. Основные понятия
Одной из основных задач дифференциального исчисления является нахождение производной функции или дифференциала заданной функции.
Первой основной задачей интегрального исчисления является обратная задача – отыскание функции по ее производной или заданному ее дифференциалу. Второй основной задачей интегрального исчисления является определение площади плоской области и объема тела вращения.
Функция
![]() называется первообразной
для функции
называется первообразной
для функции
![]() ,
если функции
и
связаны следующим соотношением:
,
если функции
и
связаны следующим соотношением:
![]() .
.
Пример. Функция
![]() вяляется первообразной для функции
вяляется первообразной для функции
![]() ,
так как
,
так как
![]() .
.
Если для данной функции существует первообразная, то она не является единственной. Так, в предыдущем примере в качестве первообразных можно взять следующие функции:
![]() ,
,
![]()
или в общем виде
![]() ,
,
где
![]() –
произвольная постоянная, так как при
любом значении
–
произвольная постоянная, так как при
любом значении
![]() .
.
В связи с этим
возникает вопрос, исчерпывает ли функция
вида
![]() все возможные первообразные для
все возможные первообразные для
![]() или существуют еще функции другого
вида, которые также будут первообразными
для
.
или существуют еще функции другого
вида, которые также будут первообразными
для
.
Ответ на него дает следующая теорема.
Теорема. Если есть какая-либо из первообразных для данной функции , то самое общее выражение для первообразной имеет вид:
![]() ,
,
где – есть первообразная постоянная.
Доказательство.
Пусть
![]() есть любая функция, имеющая своей
производной
есть любая функция, имеющая своей
производной
![]() .
.
С другой стороны, рассматриваемая функция также имеет своей производной, то есть .
Вычитая это равенство из предыдущего, имеем:
![]()
и, следовательно,
![]() ,
,
где есть постоянная, что и требовалось доказать.
Действительно,
если производная некоторой дифференцируемой
функции
![]() ,
то сама функция
,
то сама функция
![]() может быть только постоянной.
может быть только постоянной.
Полученный результат можно сформулировать и так: если производная (или дифференциалы) двух функций тождественно равны, то сами функции отличаются лишь постоянным слагаемым.
Если функция
является первообразной для
,
то семейство всех ее первообразных
функций
называется неопределенным
интегралом
от функции
и обозначается как
![]() .
.
Таким образом, по определению
![]() ,
,
если
![]() .
.
При этом функцию
называют подынтегральной
функцией,
![]() – подынтегральным
выражением,
переменную
– переменной
интегрирования,
а знак
– подынтегральным
выражением,
переменную
– переменной
интегрирования,
а знак
![]() –
знаком
интеграла.
Действие, с помощью которого по данной
функции
находим ее первообразную
,
называется интегрированием функции
.
–
знаком
интеграла.
Действие, с помощью которого по данной
функции
находим ее первообразную
,
называется интегрированием функции
.
Пример.
Найти неопределенный интеграл от функции
![]() .
.
Решение.
Первообразной от
будет функция
![]() ,
так как
,
так как
![]() .
В таком случае
.
В таком случае
![]() ,
где
– произвольная постоянная.
,
где
– произвольная постоянная.
2. Таблица основных интегралов
Степенные функции:
![]() ;
;
![]() .
.
Показательные функции:
![]() ;
;
![]() .
.
Тригонометрические функции:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Дробные рациональные функции:
![]() ;
;
![]() ;
;
![]() .
.
Иррациональные функции:
![]() ;
;
![]() ;
;
![]() .
.
3. Основные свойства неопределенного интеграла
Если
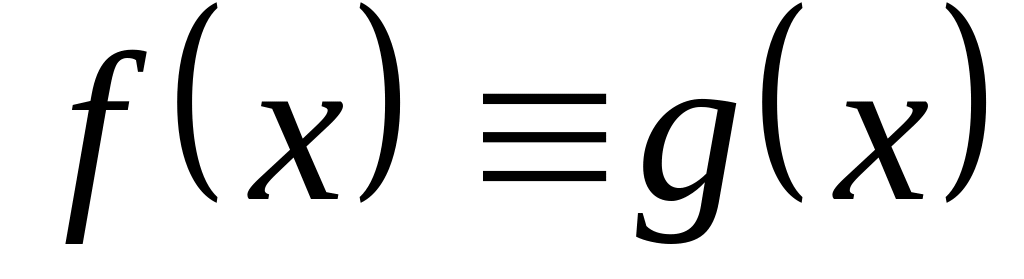 ,
то
,
то
 ,
где
– произвольная постоянная.
,
где
– произвольная постоянная.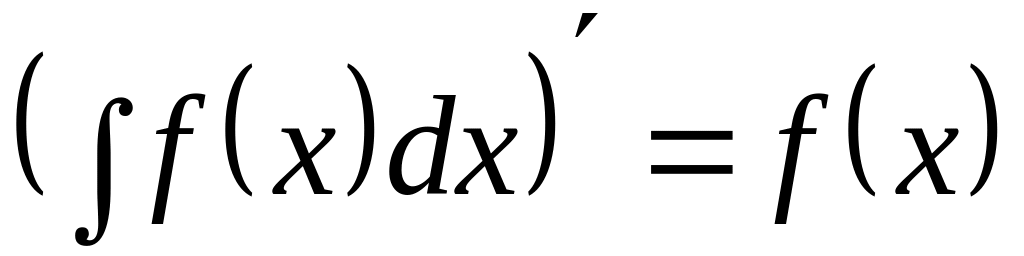 .
(1)
.
(1)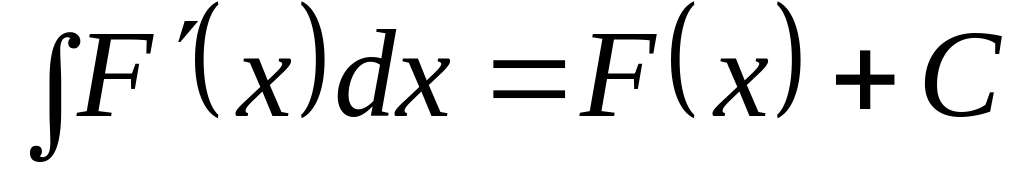 ,
где
– произвольная постоянная.
,
где
– произвольная постоянная.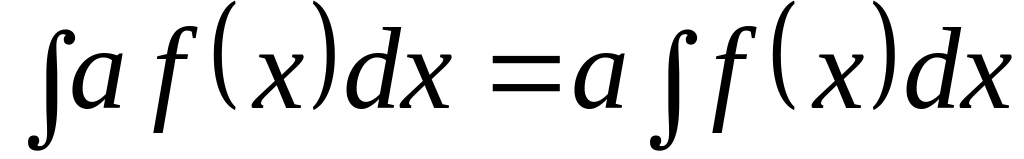 ,
,
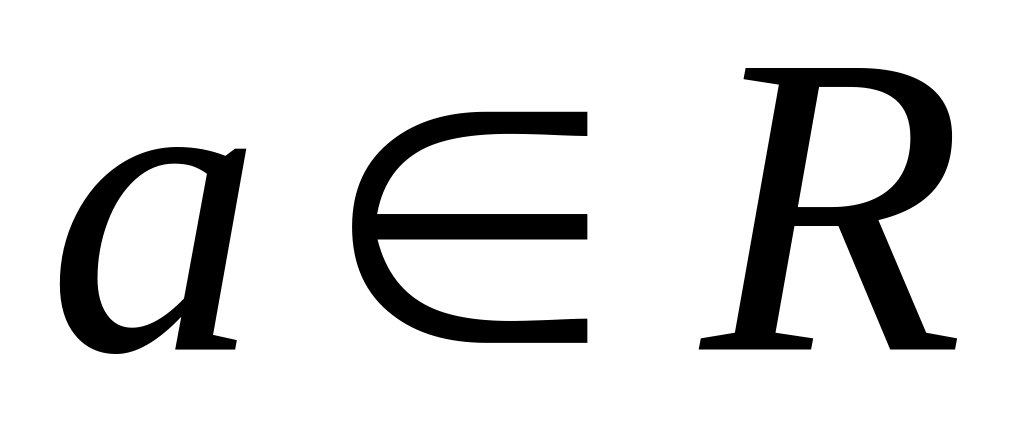 ,
,
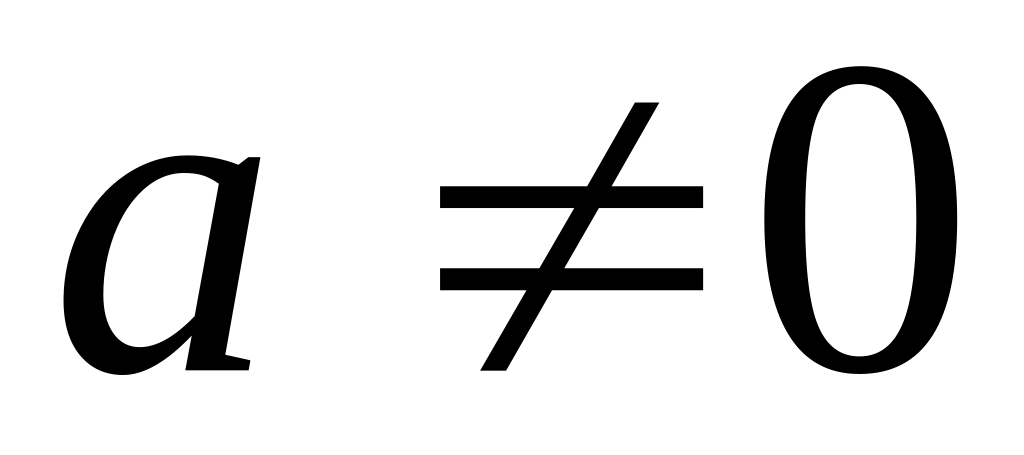 .
.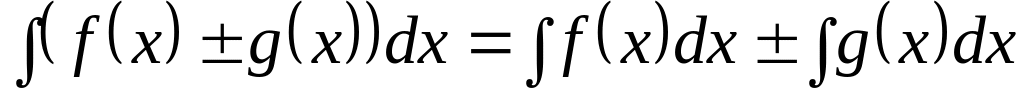 .
.
Пример.
Найти
![]() .
.
Решение.
![]()
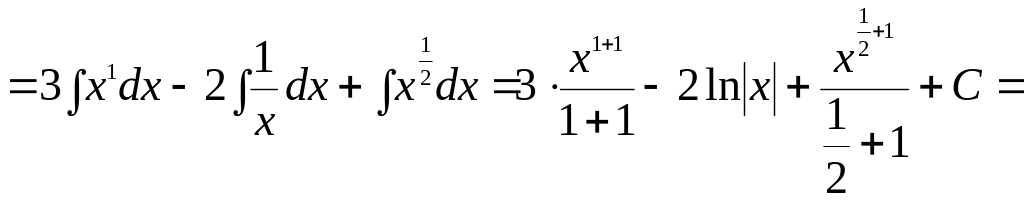
![]()
4. Простейшие способы интегрирования.
Непосредственное интегрирование
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл удается привести к одному или нескольким табличным интегралам. К табличному виду обычно удается привести не очень сложные интегралы путем элементарных тождественных преобразований подынтегральных функций, а также воспользовавшись основными свойствами неопределенного интеграла. Поясним сказанное примерами.
Пример.
Найти
![]() .
.
Решение.
![]()
![]()
![]()
Выполнив
под знаком интеграла очевидные
тождественные преобразования (возвести
разность в квадрат), свели данный интеграл
к трем табличным интегралам
![]() ,
,
![]() постоянная
(которая в данном примере равна сумме
трех постоянных
постоянная
(которая в данном примере равна сумме
трех постоянных
![]() )
появляется тогда, когда исчезают знаки
интеграла.
)
появляется тогда, когда исчезают знаки
интеграла.
Пример.
Найти
![]() .
.
Решение.
![]()
![]() .
.
