
- •П.В. Столбов Математика
- •Часть II
- •§ 1. Функция двух переменных
- •1. Основные понятия
- •2. Предел и непрерывность функции двух переменных
- •3. Частные производные и дифференцируемость функции двух переменных
- •4. Дифференцирование сложных функций
- •5. Дифференцирование неявных функций
- •6. Касательная плоскость и нормаль к поверхности
- •7. Полный дифференциал функции двух переменных и его геометрический смысл
- •8. Производная по направлению. Градиент
- •Свойства градиента
- •§ 2. Экстремумы функции двух переменных
- •1. Частные производные высших порядков. Экстремумы функции двух переменных
- •2. Наибольшее и наименьшее значение функции в замкнутой области
- •Алгоритм нахождения наибольшего и наименьшего значений дифференцируемой в области функции :
- •§ 3. Первообразная и неопределенный интеграл. Основные приемы интегрирования
- •1. Основные понятия
- •Интегрирование подстановкой.
- •Интегрирование по частям.
- •§ 4. Определенный интеграл
- •1. Задачи, приводящие к понятию определенного интеграла
- •2. Площадь криволинейной трапеции
- •3. Масса линейного неоднородного стержня
- •4. Работа переменной силы на прямолинейном участке пути
- •5. Свойства определенного интеграла
- •6. Вычисление определенного интеграла. Формула Ньютона-Лейбница
- •7. Вычисление определенного интеграла подстановкой
- •8. Вычисление определенного интеграла интегрированием по частям
- •9. Вычисление площади плоской фигуры
- •Контрольные задания
- •Задание 8.
- •Литература
- •Содержание
- •§ 1. Функция двух переменных 3
- •§ 2. Экстремумы функции двух переменных 18
- •§ 3. Первообразная и неопределенный интеграл. Основные приемы интегрирования 29
- •§ 4. Определенный интеграл 36
- •Математика
- •Часть II
- •603950, Н.Новгород, Ильинская, 65
Свойства градиента
Производная функции по направлению есть скалярное произведение градиента и единичного вектора
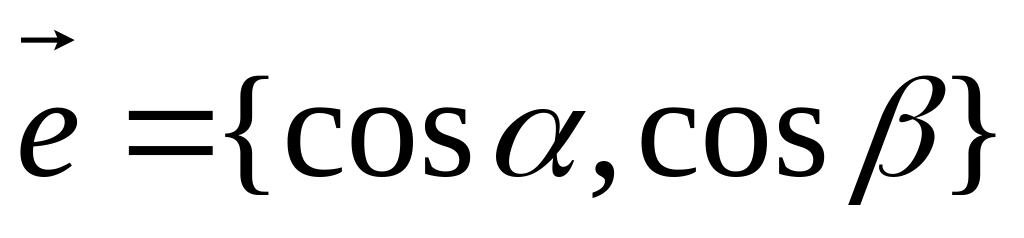 ,
задающего направление
.
,
задающего направление
.
![]()
Градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке, причем
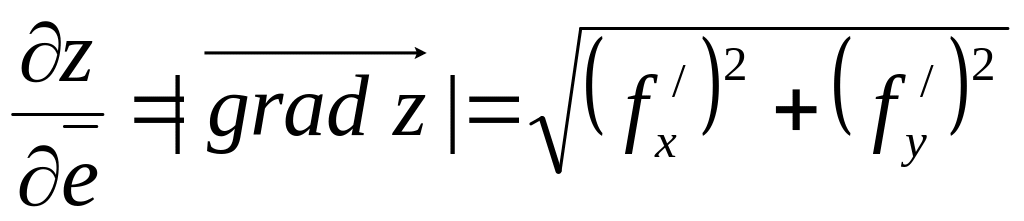 .
.Если градиент дифференцируемой функции в точке
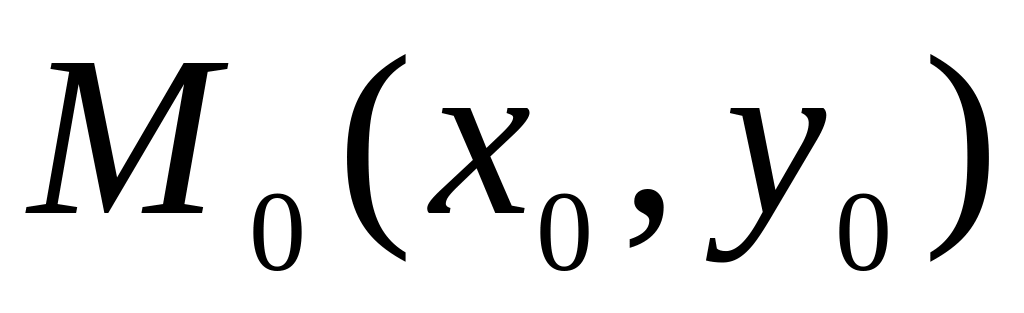 отличен от нуля, то вектор
перпендикулярен линии уровня, проходящей
через данную точку.
отличен от нуля, то вектор
перпендикулярен линии уровня, проходящей
через данную точку.
Пример. Найти градиент функции в точке М(1,2).
Решение. Находим
, ,
, .
Следовательно,
![]()
§ 2. Экстремумы функции двух переменных
1. Частные производные высших порядков. Экстремумы функции двух переменных
Если частные
производные
![]() и
и
![]() функции
сами являются дифференцируемыми
функциями, то можно найти также и их
частные производные, которые называются
частными
производными второго порядка, то
есть
функции
сами являются дифференцируемыми
функциями, то можно найти также и их
частные производные, которые называются
частными
производными второго порядка, то
есть
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Аналогично определяются частные производные 3-го, 4-го и т.д. порядков. Частная производная второго и более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Имеет место следующая теорема.
Теорема. Если
частные производные второго порядка
функции
непрерывны
в точке
,
то в этой точке смешанные частные
производные равны, то есть
![]() .
.
Пример. Найти частные производные второго порядка функции .
Решение. Так как , , то
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной.
Пусть функция
определена в некоторой окрестности
точки
.
Точка
называется
точкой
максимума (минимума)
функции
,
если существует такая
-
окрестность точки
,
что во всех ее точках
,
отличных от
,
выполнятся неравенство
![]() (
(![]() ).
).
|
На рисунке 9:
![]() – точка максимума, а
– точка максимума, а
![]() – точка
минимума функции
.
Максимум и минимум функции называются
ее экстремумами.
– точка
минимума функции
.
Максимум и минимум функции называются
ее экстремумами.
Теорема
(необходимые условия экстремума). Если
в точке
дифференцируемая
функция
имеет
экстремум, то ее частные производные в
этой точке равны нулю:
![]() ,
,
![]() .
.
Геометрически
равенства
![]() и
и
![]() означают, что в точке экстремума функции
касательная плоскость к поверхности,
изображающей функцию
,
параллельна плоскости
,
так как уравнение касательной плоскости
есть
означают, что в точке экстремума функции
касательная плоскость к поверхности,
изображающей функцию
,
параллельна плоскости
,
так как уравнение касательной плоскости
есть
![]() .
.
Замечание. Функция
может иметь экстремум в точках, где хотя
бы одна из частных производных не
существует. Например, функция
![]() имеет максимум в точке
имеет максимум в точке
![]() ,
,
![]() (см. рис. 10), но не имеет в этой точке
частных производных.
(см. рис. 10), но не имеет в этой точке
частных производных.
Рис. 10 |
Точки, в которой
частные производные первого порядка
функции
равны нулю, то есть
![]() и
и
![]() ,
и точки, в которых хотя бы одна частная
производная не существует, называются
критическими
точками.
,
и точки, в которых хотя бы одна частная
производная не существует, называются
критическими
точками.
В критических
точках функция
может иметь экстремум, а может и не
иметь. Условия
и
являются необходимыми, но не достаточными
условиями существования экстремума.
Так, например, для функции
![]() точка (0,0) является критической (в ней
точка (0,0) является критической (в ней
![]() и
и
![]() обращаются в ноль), однако, очевидно,
никакого экстремума в этой точке нет
(см. рис. 11).
обращаются в ноль), однако, очевидно,
никакого экстремума в этой точке нет
(см. рис. 11).
Рис. 11 |
Теорема
(достаточные условия экстремума). Пусть
в некоторой окрестности стационарной
точки
функция
имеет
непрерывные частные производные до
второго порядка включительно причем
![]() ,
,
![]() ,
,
![]() .
.
Обозначим
![]() .
.
Тогда:
если
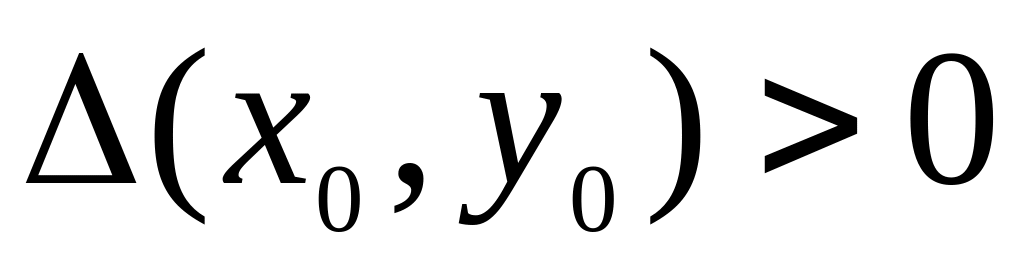 ,
то функция
в точке
имеет
экстремум: максимум, если
,
то функция
в точке
имеет
экстремум: максимум, если
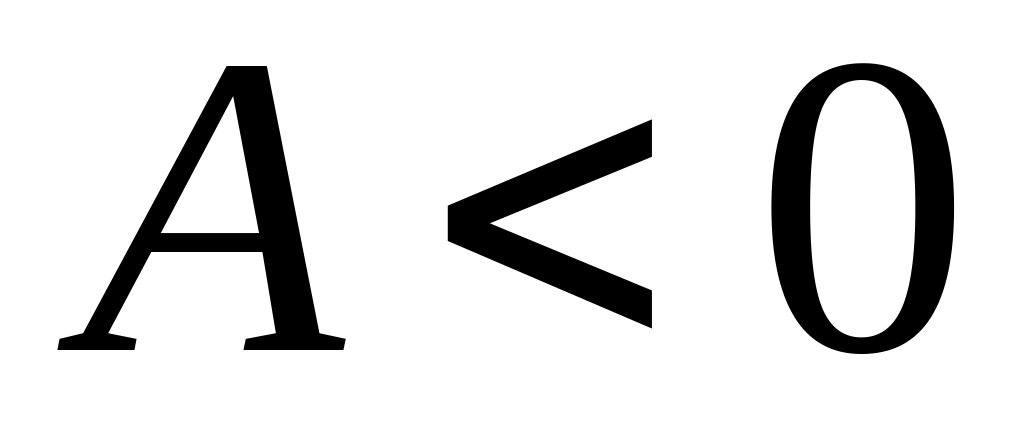 ,
и минимум, если
,
и минимум, если
 ;
;если
 ,
то функция
в точке
экстремума
не имеет;
,
то функция
в точке
экстремума
не имеет;если
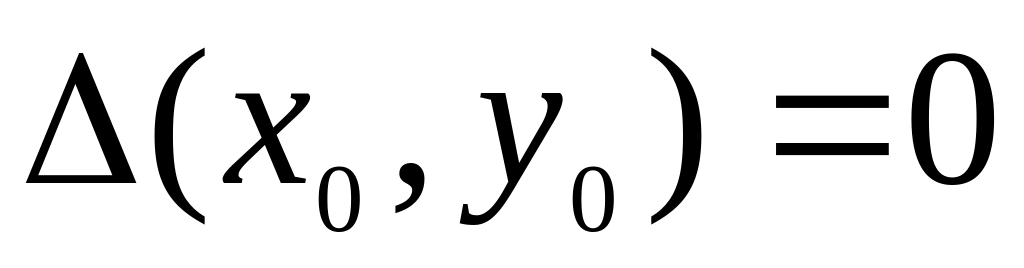 ,
то экстремум в точке
может быть, может не быть. Необходимы
дополнительные исследования.
,
то экстремум в точке
может быть, может не быть. Необходимы
дополнительные исследования.
Пример.
Найти точки экстремума функции
![]() .
.
Решение.
1) Найдем частные производные первого
порядка:
![]() ,
,
![]() .
Точки, в которых частные производные
не определены отсутствуют.
.
Точки, в которых частные производные
не определены отсутствуют.
2) Найдем стационарные точки, решая систему уравнений:
![]()
Отсюда получаем
две точки:
![]() и
и
![]() .
.
3) Находим частные
производные второго порядка данной
функции:
![]() ,
,
![]() ,
,
![]() .
.
4) В точке
![]() имеем:
имеем:
![]() ,
,
![]() ,
,
![]() ,
отсюда
,
отсюда
![]() ,
то есть
– точка экстремума. Так как
,
то есть
– точка экстремума. Так как
![]() ,
то
– точка максимума.
,
то
– точка максимума.
В точке
:
![]() ,
,
![]() ,
,
![]() ,
отсюда
,
отсюда
![]() .
Проведем
дополнительное исследование. Значение
функции
в точке
равно нулю. Рассмотрим точки из окрестности
точки
такие, что
.
Проведем
дополнительное исследование. Значение
функции
в точке
равно нулю. Рассмотрим точки из окрестности
точки
такие, что
![]() ,
тогда
,
тогда
![]() ,
а теперь рассмотрим точки из той же
окрестности, но с условием
,
а теперь рассмотрим точки из той же
окрестности, но с условием
![]() ,
,
![]() :
:
![]() .
Таким образом, в любой окрестности точки
функция
принимает как отрицательные, так и
положительные значения. Следовательно,
в точке
функция экстремума не имеет.
.
Таким образом, в любой окрестности точки
функция
принимает как отрицательные, так и
положительные значения. Следовательно,
в точке
функция экстремума не имеет.

 Рис.
9
Рис.
9
