7. Полный дифференциал функции двух переменных и его геометрический смысл

Дифференциалом дифференцируемой в точке функции называется главная линейная часть полного приращения этой функции в точке , то есть

. (1)

Если положить , то , то есть . Аналогично, полагая , получим, что . Таким образом, дифференциалы независимых переменных совпадают с приращениями этих переменных, то есть

. (2)

Геометрический смысл дифференциала: если полное приращение функции представляет геометрически приращение аппликаты поверхности , то дифференциал функции есть приращение аппликаты касательной плоскости к поверхности в данной точке, когда переменные и получают приращения и (см. рис.7).

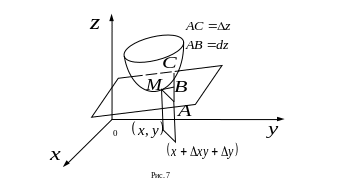
Напомним, что если функция дифференцируема в точке , то ее полное приращение в этой точке может быть представлено в виде

(3)

Из соотношений (2) и (3) следует, что при достаточно малых и имеет место приближенное равенство . Отсюда получаем формулу приближенных вычислений:

(4)

Пример. Вычислить приближенно .

Решение. Рассмотрим функцию . Тогда , где . . Воспользуемся формулой (4), предварительно найдя и :

, ,

, .

Следовательно, .

Для сравнения: используя микрокалькулятор, находим: .

8. Производная по направлению. Градиент

Пусть в области , в которой определена функция , в некоторой внутренней точке задано направление вектором (см. рис.8). Нас интересует поведение функции при движении точки в этом направлении. Пусть расстояние между точками и , а – единичный вектор заданного направления . Тогда координаты точки равны: . Если точка стремится к точке в заданном направлении, то .

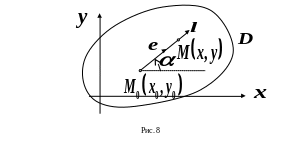
Производной функции в точке в заданном направлении называется предел

.

В частности, частные производные это производные по направлению координатных осей и соответственно. Оказывается, что для функции, имеющей непрерывные частные производные, производная по направлению выражается через частные производные в данной точке. Чтобы это доказать, нам необходимо научиться находить частные производные сложных функций.

Производная характеризует скорость изменения функции в направлении .

Теорема. Если функция дифференцируема в точке , то производная по направлению в точке определяется формулой

, (1)

где – единичный вектор заданного направления

Замечание. Если направление задано вектором , то производная функции по направлению может быть подсчитана по формуле

. (2)

Пример. Найти производную от функции в точке М(1,2) в направлении, составляющим с осью угол в .

Решение. Направление задано углом наклона к оси , поэтому воспользуемся формулой (1).

, ,

, ,

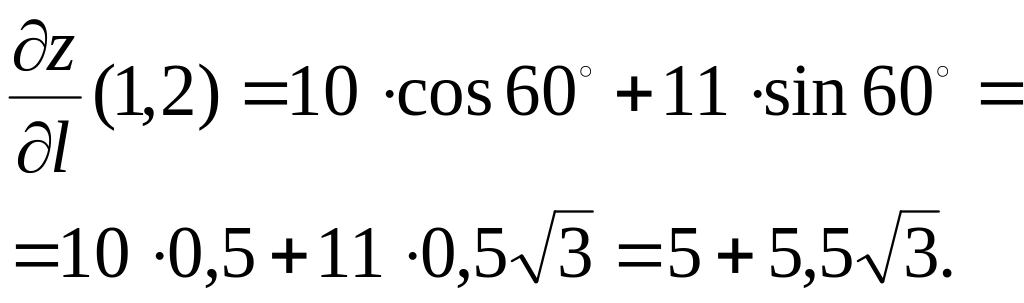
Пример. Найти производную от функции в точке М(1;2) найти производную по направлению .

Решение. Направление задано координатами вектора , поэтому воспользуемся формулой (2).

, ,

, ,

.

Рассмотрим понятие градиента функции .

Градиентом функции называется вектор с координатами .