6. Вычисление определенного интеграла. Формула Ньютона-Лейбница

Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции.

Теорема. Если – одна из первообразных непрерывной на отрезке функции , то справедлива следующая формула Ньютона-Лейбница:

. (4.1)

Доказательство. Доказательство проведем, используя свойство 7. обозначим определенный интеграл с переменным верхним пределом через функцию , т.е. . Тогда в силу свойства 7 можно записать 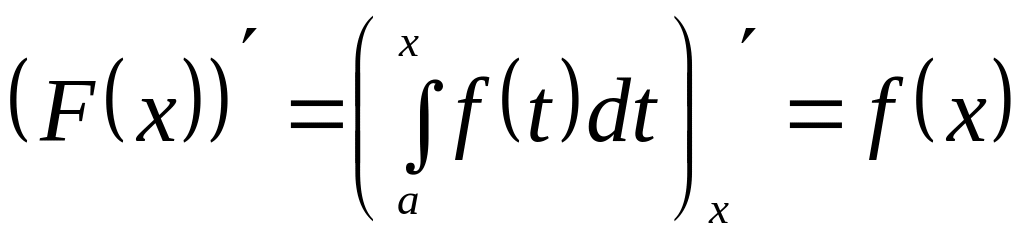. Следовательно, является одной из первообразных для интеграла . Так как, все первообразные отличаются на постоянную, то имеет место равенство , , где – некоторое число. Подставляя в это равенство значение , имеем , т.е. для любого имеем . Полагая , получаем соотношение . Обозначим разность . Тогда формулу Ньютона-Лейбница можно записать в виде . Теорема доказана.

Замечание. Из формулы Ньютона-Лейбница следует, что при вычислении определенного интеграла надо найти первообразную для подынтегральной функции и вычислить разность . Следовательно, формально все сводится к вычислению неопределенного интеграла, и здесь применимы все методы вычисления неопределенного интеграла.

Пример. Вычислить .

Решение. Взяв неопределенный интеграл и воспользовавшись формулой (4.1), решаем:

Ответ: .

7. Вычисление определенного интеграла подстановкой

Для вычисления определенного интеграла подстановкой поступают так же, как и при нахождения неопределенного интеграла подстановкой. Но при этом есть одна особенность, суть которой заключается в том, что неопределенный интеграл есть функция, а определенный интеграл есть число.

Как было показано в примере 3, для того, чтобы при помощи подстановки привести заданный неопределенный интеграл к табличному, аргумент выражают через новую переменную, затем находят неопределенный интеграл, и полученный результат снова выражают через первоначальный аргумент. В случае же определенного интеграла нет необходимости возвращаться к первоначальной переменной.

Таким образом, для вычисления определенного интеграла подстановкой пользуются формулой:

, (4.2)