Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Нижегородский государственный архитектурно-строительный университет»

-------------------------------------------------------------------------------------------------

Институт экономики, управления и права

П.В. Столбов Математика

Часть II

Утверждено редакционно-издательским

советом университета в качестве

учебного пособия

Нижний Новгород

ННГАСУ

2012

ББК 22.1

С 81

Столбов П.В. Математика. Часть II [текст]: учебное пособие / П.В. Столбов; Нижегород. гос. архит.-строит. ун-т.– Н.Новгород: ННГАСУ, 2012. – 62 с.

ISBN 978-5-87941-880-0

Учебное пособие и контрольные задания по математике предназначены для студентов заочной формы обучения всех специальностей.

ББК 22.1

ISBN 978-5-87941-880-0

© Столбов П.В., 2012

§ 1. Функция двух переменных

1. Основные понятия

Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции двух переменных, для которой можно дать наглядную геометрическую интерпретацию.

Пусть задано множество упорядоченных пар чисел плоскости .

Правило , по которому каждой паре чисел множества ставится в соответствие одно и только одно действительное число называется функцией двух переменных, заданной на множестве со значениями в и обозначается:

, .

Множество называется областью определения функции. Множество значений, принимаемых в области определения, называется областью изменения этой функции и обозначается .

При этом и называются независимыми переменными (аргументами), а – зависимой переменной (функцией).

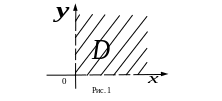
Пример. Площадь прямоугольника со сторонами, длины которых равны и является функцией двух переменных: . Область определения этой функции есть множество . (См. рис. 1).

Функцию , где можно рассматривать как функцию точки координатной плоскости . В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями.

Пример. Найти область определения функции .

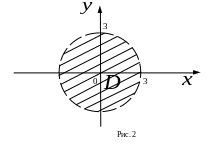
Решение. Функция существует для тех пар значений и , которые удовлетворяют неравенству или , то есть представляет собой круг, не включая границу, с центром в начале координат и радиусом .

Графиком функции двух переменных называется множество точек трехмерного пространства, представляющее собой некоторую поверхность (рис. 3), которая геометрически изображает данную функцию .

Рис. 3

Пример. Функция имеет областью определения замкнутый круг и изображается верхней полусферой с центром в точке и радиусом (см. рис. 4).

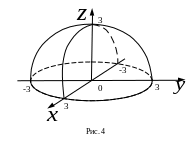
Функция двух переменных, как и функция одной переменной, может быть задана различными способами: таблицей, аналитически, графиком. Будем пользоваться аналитическим способом: когда функция двух переменных задается с помощью формулы.

Как правило, построение поверхности оказывается довольно трудной задачей. Поэтому для изучения функции используют линии уровня. Понятие линии уровня широко используется, прежде всего, в геодезии, картографии, а также при описании различных физических полей (температура, давление и пр.).

Линией уровня функции двух переменных называется кривая, на плоскости в точках которой функция сохраняет постоянное значение .

Геометрически придание функции постоянного значения означает пересечение поверхности с плоскостью , параллельной координатной плоскости .

Пример. Построить линии уровня функции .

Решение. Линии уровня данной функции – это семейство кривых на плоскости , задаваемое уравнением или . Это уравнение определяет семейство окружностей с центром в точке (0,1) и радиусом ; точка (0,1) – это вырожденная линия уровня, соответствующая минимальному значению функции (рис. 5).

Рис. 5