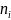- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •7. За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •7. За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •7. За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •7. За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
- •Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
- •Задано інтегральну функцію розподілу неперервної випадкової величини
- •7.За результатами вибірки, наведеними нижче потрібно:
- •9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
Варіант 1.
Інспектор перевіряє 20 підприємств, з яких 14 сплачують податки за спрощеною системою. Яка ймовірність того що з 6 навмання вибраних підприємств рівно 4 сплачують податки за спрощеною системою?
Ймовірність отримання гранту 0,18. Групою вчених було подано 7 пропозицій. Знайти ймовірність найімовірнішого числа отриманих грантів?
Ймовірність того, що користувач мережі INTERNET відвідає сайт дорівнює 0,2. Яка ймовірність того, що з 300 відвідувачів рівно 57 відвідали сайт?
Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
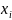
0
2
3
5
6

0,1
0,25
0,2
0,3
0,15
Випадкова величина Х розподілена за нормальним законом
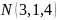 .
Обчислити ймовірність події
.
Обчислити ймовірність події
 .
.Задано інтегральну функцію розподілу неперервної випадкової величини
 ;
;

Знайти:
а) диференціальну функцію розподілу
імовірностей
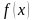 ;
б) побудувати графіки інтегральної та
диференціал функцій розподілу
ймовірностей; в) обчислити
;
б) побудувати графіки інтегральної та
диференціал функцій розподілу
ймовірностей; в) обчислити
 ,
,
 ;
г) імовірність подій:
;
г) імовірність подій:
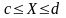 ,
д) обчислити
,
д) обчислити
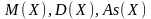 .
.
7. За результатами вибірки, наведеними нижче потрібно:
Побудувати статистичний розподіл вибірки.
Побудувати полігон та гістограму частот, відносних частот.
Знайти аналітичний вигляд емпіричної функції розподілу та побудувати її графік.
Обчислити числові характеристики вибірки: вибіркову середню, дисперсію вибірки, середньоквадратичне відхилення, моду й медіану, емпіричні початкові та центральні моменти, асиметрію та ексцес.
13, 12, 9, 11, 17, 16, 8, 14, 18, 11, 19, 20, 21, 13, 18, 16, 19, 21, 17, 16, 17, 16, 15, 14, 20, 16, 13, 14, 9, 18, 17, 15, 18, 19, 15, 14, 20, 21, 23, 24, 10, 22, 11, 20, 13, 12, 16, 17, 15, 15
8. Досліджувався місячний прибуток працівників у гривнях підприємства. Результати досліджень представлені як інтервальний статистичний розподіл. Обчислити числові характеристики вибірки за данними інтервального розподілу використовуючи метод умовних варіант: вибіркову середню, дисперсію вибірки, середньоквадратичне відхилення, моду й медіану. Використовуючи критерій Пірсона перевірити гіпотезу про нормальний закон розподілу досліджуваної величини.
Межі інтервалів, грн.. |
500-1000 |
1000-1500 |
1500-2000 |
2000-2500 |
2500-3000 |
3000-3500 |
3500-4000 |
Понад 4000 |
|
15 |
47 |
88 |
208 |
313 |
83 |
37 |
9 |
Рівень значущості γ=0,995 |
||||||||
9.
Використовуючи одно факторний дисперсійний
аналіз при рівні значущості
 з’ясувати, чи істотно впливає фактор
F
на ознаку Х.
з’ясувати, чи істотно впливає фактор
F
на ознаку Х.
Ступінь впливу фактора |
Спостережувані значення ознаки Х |
1 |
25,4; 29,3; 30,1; 28,3 |
2 |
25,7; 28,2; 30,5 |
3 |
22,3; 28,4; 29,1; 32,4 |
10. Для аналізу залежності об’єму продажу товару У (тис. у.г.о.) від маркетингових витрат Х (тис.у.г.о.) відібрана вибірка об’єму n=10, результати якої наведено у таблиці. Необхідно визначити вид залежності; використовуючи метод найменших квадратів оцінити параметри рівняння регресії У на Х; оцінити тісноту лінійної залежності між Х та У; спрогнозувати об’єм продажу при маркетингових витратах Х=хпрогноз
І |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
прогноз |
хі |
0,8 |
0,9 |
0,9 |
1,1 |
1,15 |
1,2 |
1,2 |
1,5 |
1,65 |
1,8 |
2,0 |
уі |
20 |
22 |
23 |
25 |
30 |
33 |
32 |
37 |
38 |
45 |
? |
Варіант 2
Ймовірність того, що продукт вироблено в Україні 0,95, за кордоном – 0,05. Ймовірність того, що продукт має термін зберігання більше тижня для українського та закордонного продукту відповідно 0,8 та 0,6. Навмання взятий продукт має термін придатності більше тижня. Яка ймовірність, що він український?
Ймовірність прийняття замовлення від клієнта 0,6. Було отримано 6 дзвінків. Знайти ймовірність того, що було прийнято 5 замовлень?
Ймовірність пошкодження одиниці товару під час транспонування 0,002. Перевозили 5000 одиниць товару. Яка ймовірність, що буде пошкоджено від п’яти до восьми одиниць товару?
Обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення та моду дискретної випадкової величини, що задана таблично
-1
0
1
4
5
0,5
0,12
0,1
0,2
0,08
Випадкова величина Х розподілена за біноміальним законом з параметрами
 .
Оцінити ймовірність події
.
Оцінити ймовірність події
 .
.Задано інтегральну функцію розподілу неперервної випадкової величини
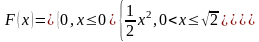 ;
;

Знайти: а) диференціальну функцію розподілу імовірностей ; б) побудувати графіки інтегральної та диференціал функцій розподілу ймовірностей; в) обчислити , ; г) імовірність подій: , д) обчислити .
7. За результатами вибірки, наведеними нижче потрібно:
Побудувати статистичний розподіл вибірки.
Побудувати полігон та гістограму частот, відносних частот.
Знайти аналітичний вигляд емпіричної функції розподілу та побудувати її графік.
Обчислити числові характеристики вибірки: вибіркову середню, дисперсію вибірки, середньоквадратичне відхилення, моду й медіану, емпіричні початкові та центральні моменти, асиметрію та ексцес.
19, 21, 18, 10, 17, 15, 8, 14, 18, 11, 19, 20, 21, 13, 18, 16, 19, 21, 17, 16, 17, 16, 15, 14, 20, 16, 13, 24, 9, 18, 17, 15, 18, 19, 15, 14, 20, 21, 23, 24, 10, 22, 11, 20, 25, 12, 16, 14, 15, 14
8. Досліджувався місячний прибуток працівників у гривнях підприємства. Результати досліджень представлені як інтервальний статистичний розподіл. Обчислити числові характеристики вибірки за данними інтервального розподілу використовуючи метод умовних варіант: вибіркову середню, дисперсію вибірки, середньоквадратичне відхилення, моду й медіану. Використовуючи критерій Пірсона перевірити гіпотезу про нормальний закон розподілу досліджуваної величини.
Межі інтервалів, грн.. |
500-1000 |
1000-1500 |
1500-2000 |
2000-2500 |
2500-3000 |
3000-3500 |
3500-4000 |
Понад 4000 |
|
16 |
38 |
79 |
169 |
195 |
77 |
41 |
10 |
Рівень значущості γ=0,99 |
||||||||
9. Використовуючи одно факторний дисперсійний аналіз при рівні значущості з’ясувати, чи істотно впливає фактор f на ознаку х.
Ступінь впливу фактора |
Спостережувані значення ознаки Х |
1 |
15; 17; 21 |
2 |
19; 18; 20; 23 |
3 |
16; 16; 18; 19 |
4 |
20; 21; 21; 23 |
10. Для аналізу залежності об’єму продажу товару У (тис. у.г.о.) від маркетингових витрат Х (тис.у.г.о.) відібрана вибірка об’єму n=10, результати якої наведено у таблиці. Необхідно визначити вид залежності; використовуючи метод найменших квадратів оцінити параметри рівняння регресії У на Х; оцінити тісноту лінійної залежності між Х та У; спрогнозувати об’єм продажу при маркетингових витратах Х=хпрогноз
І |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
прогноз |
хі |
1,05 |
1,08 |
1,1 |
1,3 |
1,35 |
1,4 |
1,45 |
1,45 |
1,6 |
2,0 |
1,5 |
уі |
20 |
22 |
23 |
25 |
30 |
33 |
32 |
37 |
38 |
45 |
? |
Варіант 3.