В дифференциальном уравнении в явном виде отсутствует независимая переменная

Третий, чуть более сложный тип уравнения, допускающий понижение порядка - отличительная особенность данного диффура состоит в том, что в нём в явном виде отсутствует независимая переменная «икс». То есть, в исходном дифференциальном уравнении нет «икса». Вообще нет. Ни одного. Нигде.

Пример 9

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям , ,

Решение: В данном уравнении в явном виде не участвует переменная . Подстановка здесь более замысловата. Первую производную  заменим некоторой пока еще неизвестной функцией , которая зависит от функции «игрек»: . Обратите внимание, что функция  – это сложная функция. Внешняя функция – «зет», внутренняя функция – «игрек» («игрек» сам по себе является функцией).

Находим вторую производную. По правилу дифференцирования сложной функции:

Учитывая, что , окончательно получаем:

В принципе, можно запомнить данную замену формально и коротко:

Другой вопрос, что студентам часто не понятно, почему в замене такая странная вторая производная: , «совершенно же очевидно, что должно быть ». А вот, оно, и не очевидно.

Итак, в исходном уравнении  проведём нашу замену:

Цель замены – опять же понизить порядок уравнения:

Одно «зет» сразу сокращаем:

Получено уравнение с разделяющимися переменными. Если – функция, зависящая от «игрек», то первая производная в дифференциалах расписывается так: . Не допускаем машинальной ошибки – не пишем «привычное» !!!

Разделяем переменные и интегрируем:

Проведем обратную замену :

Как и в первом параграфе, константу целесообразно отстрелить незамедлительно, это значительно упростит дальнейшее интегрирование.

Используем оба начальных условия одновременно: ,

В полученное уравнение  подставим  и :

Таким образом:

Дальнейшее просто:

Вторую константу тоже отстреливаем. Используя начальное условие , проводим подстановку :

Таким образом:

Выразим частное решение в явном виде:

Ответ: частное решение:

Для закрепления материала пара заключительных примеров.

Пример 10

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям , ,

Решение: В данном уравнении в явном виде не участвует переменная . Еще здесь нет первой производной, но это не должно смущать – важно, что нет «иксов», а значит, используется стандартная замена:

Таким образом, степень уравнения понижена до первого порядка:

Разделяем переменные и интегрируем, не забывая, что :

Переобозначим константу  через : .

Проведём обратную замену :

Используем одновременно оба начальных условия ,  и найдём значение константы . Для этого в полученное уравнение  подставим  и :

Таким образом:

Разделяем переменные и интегрируем:

В соответствии с начальным условием :

Окончательно:  или

Ответ: частное решение:

Пример 11

Найти решение задачи Коши. , ,

Это пример для самостоятельного решения.

Обратите внимание, что все три примера последнего параграфа идут с задачей Коши. Это не случайно. Специфика рассмотренного типа дифференциальных уравнений такова, что если предложить найти общее решение, то в большинстве уравнений нарисуются сложные,  вычурные, а то и вообще неберущиеся интегралы. Поэтому практически всегда вам будет предложено найти частное решение.

Решения и ответы:

Пример 2:

Решение: Преобразуем уравнение: Данное ДУ имеет вид . Дважды интегрируем правую часть: Ответ: общее решение:

Пример 4:

Решение: Преобразуем уравнение: Данное уравнение имеет вид . Трижды интегрируем правую часть: В соответствии с начальным условием: В соответствии с начальным условием:

В соответствии с начальным условием: Ответ: частное решение:

Пример 6:

Решение: В данное уравнение в явном виде не входит функция , проведем замену: Получено линейное неоднородное уравнение первого порядка. Используем метод вариации произвольной постоянной. Решим вспомогательное уравнение: Разделяем переменные и интегрируем: В неоднородном уравнении проведем замену: Таким образом: Обратная замена: Ответ: Общее решение:

Пример 8:

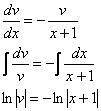
Решение: Проведем замену: Получено линейное неоднородное уравнение, замена: Составим и решим систему: Из первого уравнения найдем :  – подставим во второе уравнение: Таким образом: Обратная замена: Дважды интегрируем правую часть: Интеграл от логарифма берётся по частям, и, строго говоря, последний интеграл нужно расписать подробнее. Ответ: общее решение:  

Пример 11:

Решение: В данном уравнении в явном виде не участвует переменная , проведем замену: Обратная замена: В соответствии с начальными условиями , : В соответствии с начальным условием : Ответ: частное решение: