6 Лабораторная работа № 6 Системы линейных одновременных уравнений

Цель изучения темы: научиться оценивать параметры систем взаимозависимых эконометрических моделей с помощью косвенного и двухшагового методов наименьших квадратов.

Контрольные вопросы:

1. Каковы основные причины использования систем одновременных уравнений.

2. Назовите возможные способы построения систем уравнений. Чем они отличаются друг от друга?

3. В чем состоит основное различие между структурными уравнениями системы и уравнениями в приведенной форме.

4. В чем состоят проблемы идентификации модели и какие условия идентификации вы знаете.

5. В чем состоит суть косвенного метода наименьших квадратов.

6. В чем состоит суть двухшагового метода наименьших квадратов.

Задания: Для модели заданной в приложении Е по данным приложения Ж для своего варианта выполните следующие задания:

1 Построить модель вида , рассчитав соответствующие структурные коэффициенты.

2 Оценить параметры моделей представленных в приложении Е.

3 По полученным результатам сделайте экономический вывод.

Реализация типовых заданий:

1) Построить модель вида, рассчитав соответствующие структурные коэффициенты. Исходные данные представлены в таблице 6.1.

Составим систему структурных уравнений:

.

Для выбора метода оценки параметров проверим систему на идентифицируемость.

Таблица 6.1 – Исходные данные для построения системы взаимозависимых уравнений

Годы	Годовое потребление свинины на душу населения, кг	Оптовая цена за 1 кг свинины, р.	Доход на душу населения, р.	Расходы по обработке мяса, % к цене
1	60	5,0	1300	60
2	62	4,0	1300	56
3	65	4,2	1500	56
4	62	5,0	1600	63
5	66	3,8	1800	50
Итого	315	22,0	7500	285

Необходимое условие:

В модели 2 предопределенные переменные: , и такое же количество эндогенных переменных: и . Следовательно, М=2 и К=2.

Проверим необходимое условие для каждого уравнения системы.

Для первого уравнения:

k₁=2; m₁=1

M-m₁=1=k-1=1 следовательно, уравнение точно идентифицировано.

Для второго уравнения:

k₂=2; m₂=1

M-m₂=1=k-1=1 следовательно, уравнение точно идентифицировано.

Так как оба уравнения точно идентифицированы, система в целом тоже точно идентифицирована.

Достаточное условие:

Для того чтобы уравнение было точно идентифицируемым, достаточно чтобы ранг матрицы А (матрица коэффициентов при переменных, не входящих в данное уравнение) был равен (К-1).

Так в нашем примере система состоит только из двух уравнений, то данное условие не проверяется.

Для определения параметров точно идентифицированной модели применяется КМНК.

На первом этапе структурную форму преобразуем в приведенную форму:

.

Параметры модели А₁₁, А₁₂, А₂₁, А₂₂ определяются с помощью традиционного МНК. Найдем данные параметры используя функцию Excel Сервис – Анализ данных – Регрессия (при этом необходимо учесть, что в уравнениях отсутствует свободный член). Результаты регрессионного анализа приведенной формы представлены на рисунке 6.1.

Рисунок 6.1 – Результаты регрессионного анализа уравнений

приведенной формы

Следовательно, приведенная форма примет вид:

.

На следующем этапе определим коэффициенты структурной модели.

В первом уравнении структурной формы в правой части присутствуют переменные и . Следовательно, необходимо из второго уравнения выразить переменную через переменные и . Получим: . Подставим полученное выражение в первое уравнение и приведем подобные слагаемые:

.

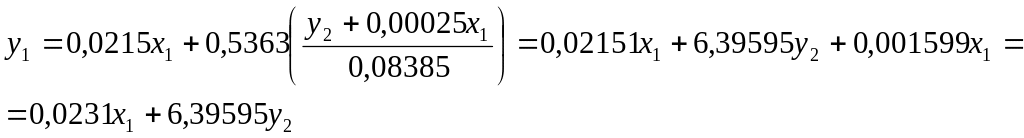Во втором уравнении структурной формы в правой части присутствуют переменные и . Следовательно, необходимо из первого уравнения выразить переменную через переменные и . Получим: . Подставим полученное выражение в первое уравнение и приведем подобные слагаемые:

.

Таким образом, структурная форма модели примет вид:

Рассчитаем по полученным уравнениям теоретические значения и . Результаты расчетов представлены на рисунке 6.2.

Рисунок 6.2 – Фактические и расчетные значения переменных и