Реализация типовых заданий

1 Проверить наличие нелинейной связи между результативным признаком и незначимыми факторами по исходным данным лабораторной работы № 1 и рассчитайте параметры уравнений: степенной; показательной; гиперболической регрессии

Степенная модель регрессии

Уравнение степенной модели имеет вид: . Для оценивания параметров необходимо провести процедуру линеаризации переменных путем логарифмирования обеих частей уравнения: . Введем новые переменные: . Тогда уравнение примет вид множественной линейной регрессии: . Для нахождения параметров данного уравнения воспользуемся инструментом анализа данных Регрессия (см. лабораторную работу № 1).

Для расчетов параметров используем данные следующей таблицы (рисунок 4.1).

Рисунок 4.1 – Исходные данные для степенной модели

Результаты регрессионного анализа представлены на рисунке 4.2.

Рисунок 4.2 – Результат применения инструмента Регрессия

Полученное уравнение множественной линейной регрессии будет иметь следующий вид: .

Оценивая параметры данного уравнения, замечаем, что статистически значимым является параметр при X1, (об этом свидетельствует величина р – значение из рисунка 4.2) следовательно, целесообразно строить уравнение степенной регрессии только с данным фактором. В результате получаем равнение следующего вида: (рисунок 4.3).

Рисунок 4.3 – Результат применения инструмента Регрессия

Потенцируя параметр уравнения, получим a=0,93. Следовательно, уравнение примет вид: .

Подставляя в данное уравнение фактические значения x₁, получаем теоретические значения результата (рисунок 4.4 графа 6). По ним рассчитаем показатели:

- тесноты связи – индекс корреляции ;

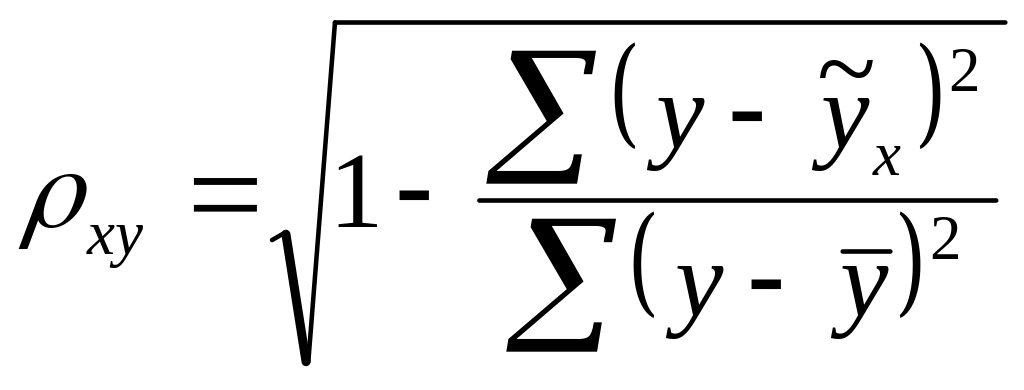- коэффициент эластичности ;

- среднюю ошибку аппроксимации ;

- F-критерий Фишера .

Рисунок 4.4 – Данные для расчета показателей по степенной модели

Индекс корреляции (рисунок 4.4) – связь между признаками средняя.

Коэффициент эластичности .

Ошибка аппроксимации (рисунок 4.4 графа 9) .

F-критерий Фишера (рисунок 4.4) .

Полученные характеристики указывают, что данная модель является удовлетворительной, но по F-критерию статистически значимой и теснота связи между признаками сильная.

Показательная модель регрессии

Построению уравнения показательной кривой предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:

,

где .

Значения параметров уравнения регрессии определим аналогично степенной модели. Для их расчета используем данные таблицы (рисунок 4.5):

Рисунок 4.5 – Исходные данные для построения показательной модели

Результаты регрессионного анализа представлены на рисунке 4.6.

Рисунок 4.6 – Результат применения инструмента Регрессия

Получено уравнение множественной линейной регрессии: .

Оценивая параметры данного уравнения, замечаем, что статистически значимым является параметр при X1, (об этом свидетельствует величина р – значение из рисунка 4.6) следовательно, целесообразно строить уравнение показательной регрессии только с данным фактором. В результате получаем равнение следующего вида: (рисунок 4.7).

Произведем потенцирование полученного уравнения и запишем его в обычном виде: .

Подставляя в данное уравнение фактические значения x₁, получаем теоретические значения результата (рисунок 4.8 графа 6). По ним рассчитаем показатели:

- индекс корреляции составит (рисунок 4.8): - связь между признаками сильная;

- коэффициент эластичности ;

- средняя ошибка аппроксимации (рисунок 4.8, графа 9)

;

Рисунок 4.7 – Результат применения инструмента Регрессия

- F-критерий (рисунок 4.8).

Рисунок 4.8 – Данные для расчета показателей по показательной модели

Данная модель также статистически значима и имеет удовлетворительное качество.