66.Визначення координат осі свердловини за методом середнього кута.

За цим методом використовують середні значення зенітних та азимутальних 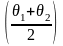кутів. Це простий метод і являє собою спосіб точних розрахунків ствола свердловини.

Таким чином приріст глибини визначають за формулою

. (169)

Приріст горизонтального зміщення визначають за формулою

. (170)

Приріст координати на північ визначають за формулою

. (171)

Приріст координати на схід визначають за формулою

. (172)

При умові не дуже великої віддалі між точками заміру у порівнянні з кривизною ствола, цей метод дозволяє легко, але і достатньо точно обчислити координати ствола свердловини.

67.Визначення координат осі свердловини за методом мінімальної кривизни.

Цей метод найточніший, він ефективно замінює ділянку реальної кривої ствола між двома точками заміру сферичною дугою. Даний метод використовує принцип мінімізації загальної кривизни розглядуваного інтервалу ствола свердловини (рисунок 76).

Це призводить до розрахунку пологої колоподібної дуги. Для виположування траєкторії ствола свердловини між двома точками заміру вводять коефіцієнт пропорціональності (Довжина заміряється по кривій, а кути та визначають напрямками прямих у просторі. Для суміщення цих прямих із сегментами кривої використовують коефіцієнт пропорціональності).

Рисунок 76 – Схема для розрахунку координат осі свердловини за методом мінімальної кривизни

Коефіцієнт пропорціональності визначається кривизною ділянки ствола свердловини :

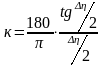, (178)

де – зміна просторового кута

.

Рівняння, одержані при використанні методу мінімальної кривизни, подібні до рівнянь балансно-тангенціального методу.

Для того, щоб одержати рівняння приросту координат за методом мінімальної кривизни необхідно рівняння, одержані методом тангенціальної рівноваги помножити на коефіцієнт пропорціональності , щоб врахувати ефект виположування.

Таким чином, маємо:

Приріст глибини:

. (179)

Приріст горизонтального зміщення:

. (180)

Приріст координати на північ:

. (181)

Приріст координати на схід:

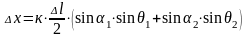. (182)

68.Визначення координат осі свердловини за методом радіуса кривизни.

Суть даного методу полягає у підобрі циліндра таких розмірів, при яких можна було б дві точки заміру розташувати на його поверхні так, щоб ділянка ствола свердловини була зігнута у вертикальній та горизонтальній площинах і лежала на поверхні циліндра (рисунок 73).

У цьому методі використовують значення зенітних та азимутальних кутів ствола для розрахунку просторової кривої, яка проходить через точки заміру. Цей метод допускає плавність викривлення ствола, він менш чутливий до різких змін осі свердловини.

Припустимо, що ділянка ствола свердловини між двома точками заміру представлена відрізком «ab» (рисунок 74)

Рисунок 73 – Схема для розрахунку координати осі свердловини за методом радіуса кривизни

Інтенсивність викривлення дорівнює відношенню приросту кутів до довжини інтервалу

,

де , – зенітні кути на початку та в кінці інтервалу, радіан.

Рисунок 74 ­– Схема для розрахунку координат осі сердловини за методом радіуса кривизни при збільшенні азимута

а – вертикальний переріз, б – горизонтальний (вид зверху) переріз

Радіус кривизни відрізка ab є величина обернена до інтенсивності викривлення.

.

Перевівши радіани в градуси одержимо:

.

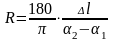З рисунка 74, а маємо:

,

.

Таким чином, приріст глибини

,

. (173)

З рисунка 74, б приріст відхилення дорівнює відрізку cb

,

,

,

.

Підставивши замість 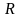його значення, одержимо приріст горизонтального зміщення:

. (174)

Відстань , або відхилення викривлення, тобто радіус кривизни в горизонтальній площині, визначають таким чином (рисунок 75).

,

де , – азимутальні кути в радіанах, заміряні в точках a та b.

Перевівши радіани в градуси, одержимо:

.

Підставивши замість його значення, одержимо:

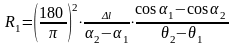. (176)

Згідно з рисунком 75, на якому представлені проекції осі свердловини на горизонтальну площину ( вид свердловини зверху), координати на північ та схід 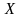визначають таким чином :

Приріст координат на північ 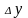(рисунок 75, а):

,

,

.

Підставивши значення радіуса , одержимо приріст координат на північ:

. (177)

Аналогічно знаходимо і приріст координат на схід (рисунок 75, б):

,

,

.

Підставивши значення радіуса , одержимо приріст координат на схід:

. (178)