63.Методи визначення координат осі свердловини за даними інклінометри.

При бурінні похилоскерованих свердловин через певні інтервали (10 м, 30 м (100 футів)) проводять заміри зенітних та азимутальних кутів. Якщо виявляють вдхилення осі свердловини від проектного профілю, то вживають заходи для коригування траєкторії. Фактичні дані кривизни забезпечують одержання наочного зображення траєкторії свердловини. Ці дані наносять на графік проектної траєкторії свердловини.

Для того, щоб встановити місцезнаходження вибою, необхідно визначити координати осі свердловини, для розрахунку яких необхідно знати такі три величини: зенітний кут, азимутальний кут та довжину ствола свердловини.

У задачах направленого буріння для визначення координат осі свердловини використовують різні методи, найпоширенішими з яких є такі

1. Тангенціальний метод.

2. Балансно-тангенціальний метод або метод тангенціальної рівноваги.

3. Метод середнього кута.

4. Метод радіуса кривизни.

5. Метод мінімальної або найменшої кривизни.

6. Метод Меркюрі або «ртутний» метод.

Метою розрахунку є визначення глибини свердловини по вертикалі «z», горизонтального зміщення « » та орієнтації свердловини на північ « » та на схід « » при новому положенні ствола. Розглянемо кожний із наведених методів.

64.Визначення координат осі свердловини за тангенціальним методом.

Цей метод грунтується на використанні зенітного та азимутального кутів в кінці інтервалу. При цьому вважають, що кінці і ділянки ствола повинні бути дотичними лініями стосовно напрямів, які задаються кутами останнього та передостаннього замірів (рисунок 71). Проте, на будь-якій ділянці викривлення реальний профіль свердловини не вписується у ці припущення і не забезпечує реального відображення дійсності за винятком, ділянок з витриманим нахилом та напрямком.

Рисунок 71 – Схема для розрахунку координат осі свердловини за тангенціальним методом

а, б – вертикальний і горизонтальний (вид зверху) переріз

Приріст глибини знаходять за формулою

. (161)

Приріст горизонтального зміщення знаходять за формулою

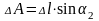. (162)

Приріст координати на північ знаходять за формулою

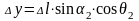. (163)

Приріст координати на схід знаходять за формулою

. (164)

Тангенціальний метод є найстаріший, найпростіший та найменш точний. Розрахунки на його основі призводять до завищеного горизонтального і заниженого вертикального зміщення. Похибки пропорціональні величинам заміряних кутів та довжині траєкторії.

65.Визначення координат осі свердловини за балансно-тангенціальним методом (ме­тодом тангенціальної рівноваги).

У цьому методі використовують заміряні кути на початку та у кінці інтервалу свердловини. За цим методом ділянку кривої між точками заміру поділяють на дві рівні частини і вважають, що верхня її частина прямолінійна і нахилена до вертикалі під кутом і має азимут , а нижня – також прямолінійна і нахилена до вертикалі під кутом і має азимут (рисунок 72). Це призводить до збалансованих розрахунків кривизни і, як наслідок, до згладжування (вирівнювання) профілю ствола свердловини.

Приріст глибини визначають за формулами:

Рисунок 72 – Схема для розрахунку координат осі свердловини за методом тангенціальної рівноваги

а, б – вертикальний і горизонтальний (вид зверху) переріз

,

. (165)

Приріст горизонтального зміщення визначають так:

,

. (166)

Приріст координат на північ визначимо за такими формулами:

,

,

,

,

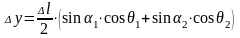. (167)

Приріст координат на схід визначаємо за такими формулами:

,

,

,

. (168)

Основна причина вищої точності балансно-тангенціального методу полягає в тому, що при обчисленні конфігурації ствола свердловини, яка змінює зенітний та азимутальний кути, похибки поточного обчислення компенсуються наступним. На ділянці набору кута помилки намагаються завищити значення глибини 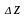і зменшити величину горизонтального зміщення . Проте, незважаючи на те, що точність даного методу така ж як і точність методу середнього кута, зазвичай цей метод застосовують значно рідше через складніші формули.