2.2. Затримка поширення радіосигналу в нейтральній атмосфері

Довжину траси електромагнітного променя в атмосфері, і зокрема у нейтральній атмосфері, називають електромагнітною довжиною шляху, і виражають як:

, (2.18)

де - диференційний елемент довжини вздовж шляху променя.

На рис. 6 показано шлях електромагнітного променя, що проходить через нейтральну атмосферу.

Рис. 6. Траєкторія променя в нейтральній атмосфері

Електромагнітний промінь наближаючись до земної поверхні буде проходити через атмосферні шари з різними показниками заломлення; отже, його траєкторія буде змінювати свій напрямок, прагнучи при цьому зберегти першопочатковий напрямок. У результаті вона буде вигнутою і направлена опуклістю догори.

Прямолінійний шлях променя або геометрична довжина шляху визначається як:

, (2.19)

тут інтегрування проводиться в умовах вакууму.

Затримку поширення нейтральної атмосфери, , визначають як різницю між електромагнітною та геометричною довжиною шляху:

. (2.20)

Ця термінологія не є універсальною і в літературі зустрічаються різні терміни, наприклад, атмосферна затримка поширення сигналу, тропосферна затримка (поширення сигналу), тропосферна рефракція, затримка шляху тощо. Деякі з цих термінів, слідуючи за назвою, можуть трактуватися обманливо, тому рекомендується відділяти дві складові, наведені в рівнянні (2.20).

Нехай S буде геометрична довжина електромагнітного шляху, яким слідує промінь, а саме:

. (2.21)

Застосовуючи рівняння (2.20) отримують:

або

. (2.22)

У цьому рівнянні перший член правої частини є надлишок довжини шляху в зв'язку із затримкою, кваліфікованою сигналом, або просто надлишкова затримка шляху (помилка діапазону), ; другий член є затримкою, викликаною викривленням променя, названою геометричною затримкою, . Таким чином, як трактується в роботі [17], визначення затримки поширення нейтральної атмосфери охоплює як надлишкову затримку шляху (хоча деякі автори використовують цей термін включаючи геометричну затримку) так і геометричну затримку. Термін тропосферна затримка часто використовується для позначення затримки нейтральної атмосфери, оскільки тропосфера вносить основний вклад у загальну величину затримки нейтральної атмосфери, а волога складова її повністю формується саме тропосферою. Оскільки термін «рефракція» включає в себе надлишкову затримку шляху і кривину променя, він також добре працює в якості альтернативи позначення до затримки поширення сигналу.

Поділ затримки поширення сигналу нейтральної атмосфери на дві компоненти є вигідним, оскільки геометрична затримка є значною лише для радіо-сигналів, що надходять при низьких кутах підвищення (нижче 10°); крім того, для горизонтально-шаруватої атмосфери S і G є ідентичними в зенітному напрямку , де геометрична затримка дорівнює нулю. Інтегральний вираз затримки поширення сигналу нейтральної атмосфери з розрахунку двох компонент має наступний вигляд:

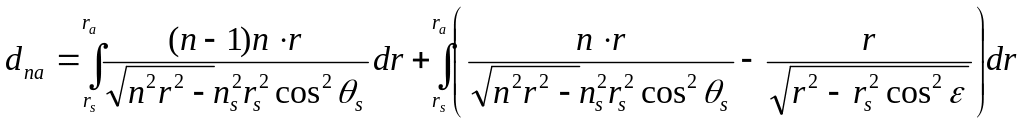, (2.23)

де - видимий (спотворений рефракцією) кут підвищення;

- геометричний (істинний) кут підвищення.

Загалом, пряме інтегрування рівняння (2.23) не представляється можливим, оскільки профіль показника заломлення уздовж шляху променя не є відомим. Тому повинно проводитись числове інтегрування дискретних значень показника заломлення профілю (якщо є такі значення) або апроксимуватись аналітично певною моделлю.

Перш ніж розглядати аналітичні апроксимації (моделювання), розглянемо окремий випадок, для якого вхідний сигнал надходить у зенітному напрямку ( ). У цьому випадку, при допущенні сферично-симетричної атмосфери, промінь не є викривленим і рівняння (2.23) приймає вигляд:

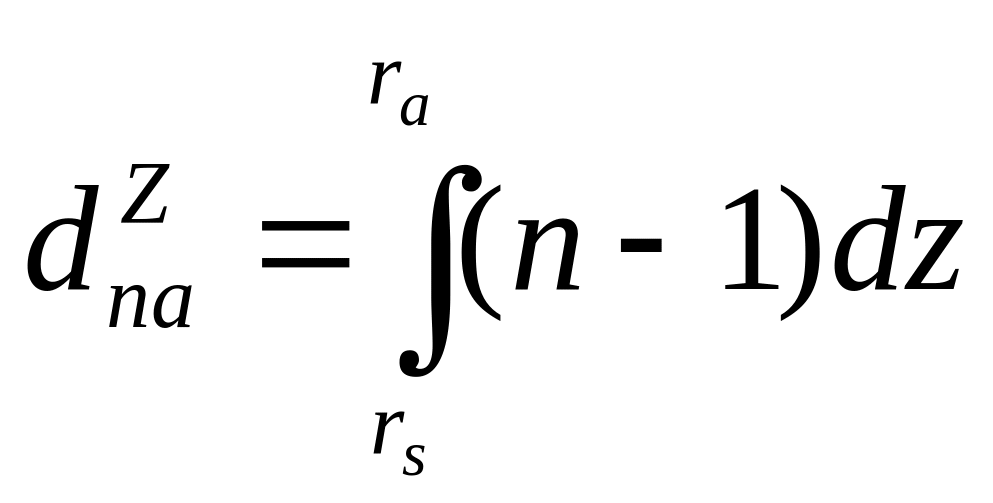, (2.24)

або

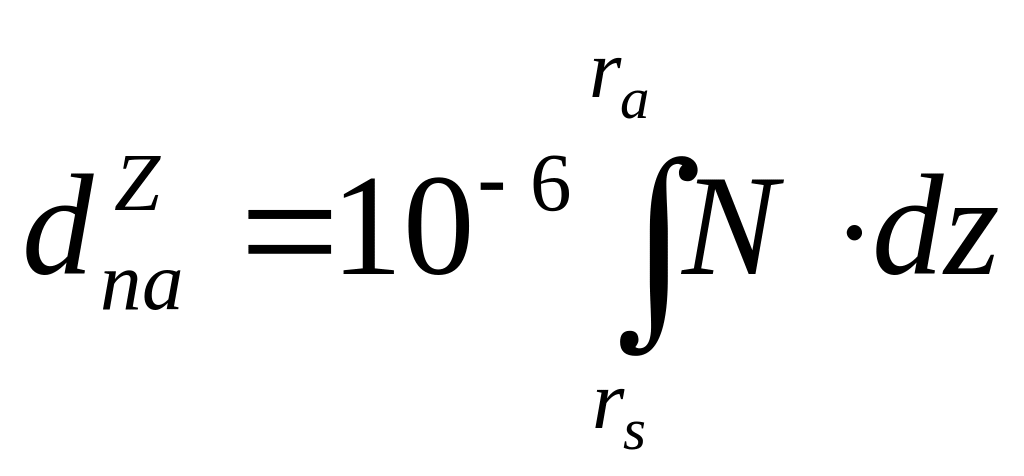. (2.25)

Визначена затримка за формулами (2.24) або (2.25) називається загальна зенітна затримка нейтральної атмосфери, або зенітна тропосферна затримка. Якщо прийняти до уваги показник заломлення, що складається з гідростатичної і негідростатичної (вологої) компонент, то зенітна тропосферна затримка також може бути розділена на дві складові – зенітна гідростатична затримка і зенітна негідростатична (волога) затримка (або суха і волога затримки, якщо беруться за основу відповідні формули індексу показника заломлення). При такому підході, рівняння (2.25) прийме вигляд:

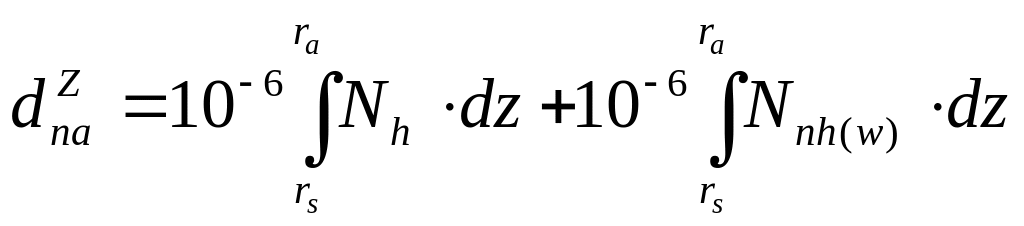, (2.26)

або у символах

, (2.27)

де представляє зенітну гідростатичну складову, а - зенітну негідростатичну (вологу) складову.

У випадках, коли сигнал поступає в позазенітному напрямку (а це абсолютно переважаючі випадки) затримка поширення нейтральної атмосфери для будь-якого кута підвищення може бути обчислена через зенітну затримку наступним виразом:

. (2.28)

Затримка поширення, отримана з використанням "закону косеканса", є очевидно, не дуже точною, оскільки вона опирається на такі "хибні" припущення, як плоскість землі і сталість рефракції. Тим не менш, можна припустити, що це можливо, щоб виразити затримку поширення сигналу нейтральної атмосфери у вигляді результату множення зенітної затримки і функції, яка відносить цю затримку до затримки на інших кутах піднесення. Таким чином, така затримка виражається як:

. (2.29)

Цей вираз визначає функцію відображення, . Ця специфічна функція відображення відображає загальну зенітну затримку. Оскільки зенітна затримка може бути виражена у вигляді суми двох компонент, функції відображення можуть бути розроблені для того, щоб відображати окремо гідростатичну і негідростатичну (вологу) компоненти. Таким чином, в цілому маємо:

, (2.30)

де - гідростатична функція відображення, а - негідростатична (волога) функція відображення.