15. Расчет по упрощенным формулам

Положим в основу расчета широко распространенную формулу Шези-Павловского-Маннинга скорость:

V = 1/n ∙ R^y ∙ (R · i)^0,5 ,

где n – коэффициент шероховатости; по нормам [1] при расчете самотечных сетей n = 0,014; для напорных трубопроводов n = 0,013;

R – гидравлический радиус;

i – уклон.

По упрощенной формуле Павловского при R < 1 y = 1,5 n^0,5;

y = 1,5 · (0,014)^0,5 = 0,177; по формуле Маннинга y = 0,167.

Примем в расчетах у = 0,17, с учетом уравнения неразрывности потока

Q = ω · R^0,67 /n (11)

Площадь живого сечения ω можно представить в виде ω = 0,25 π·D²· β,

где β – коэффициент, зависящий от величины относительного наполнения.

Используя формулу (1) определим β = (γ – cos γ · sin γ)/π , γ = arccos(1 – 2h/D); в пределах h/D 0,2…0,8 достаточно точно коэффициент β линейно зависит от h/D: β = 1,22 h/D – 0,1123 (рис. 16). Коэффициент корреляции К = 0,9997.

Рис. 17. Зависимость коэффициента

Α0,67β от наполнения

Рис. 16. Зависимость коэффициента

Β от наполнения

Гидравлический радиус R можно выразить как функцию диаметра

R = α ∙ D,

где α – коэффициент, зависящий от величины h/D;

из формулы (2) α = 0,25 (γ – cos γ · sin γ) / γ.

Формула (11) примет вид:

Q = 0,25π · D^2,67 α^0,67 β / n . (12)

Произведение коэффициентов α^0,67∙β можно аппроксимировать линейной зависимостью α^0,67∙β = 0,631· h/D – 0,1151 (рис. 17).

Если наполнение h/D находится в пределах 0,2…0,8 коэффициент корреляции К = 0,9982.

Принимая n = 0,014, получим расход

Q = 56,1· D^2,67(0,631 · h/D – 0,1151) i ^0,5; (13)

скорость V = Q/ω = 4Q / [3,14· D² (1,22 · h/D – 0,1123)]. (14)

15.1. Последовательность расчета

Сначала используют формулы (8,б), (9) и (10) для ориентировочного определения минимально необходимого уклона и диаметра:

i_мин ≈ 0,001/Q^0,372, i_ж= (z_лн – z_лк) / L, D ≈ 0,33 (Q/ )^0,35 (Q, м³/с).

Затем, после выбора стандартного диаметра, следует применить уточняющие формулы (13) и (14) для расчета наполнения и скорости.

Пример.

На участке коллектора проходящего по улице с малым уклоном, известен расход 0,025 м³/с, требуется определить диаметр и уклон трубы так, чтобы соблюдалась самоочищающая скорость.

По формуле (8б) i _мин ≈ 0,001/0,025^0,372 = 0,0039.

По формуле (10) D ≈ 0,348 (0,025 / 0,0039^0,5)^0,375 = 0,234 м.

Принимаем стандартный диаметр D_ст = 0,25 м.

По формуле (13) определяется наполнение:

h/D = [Q / (56,1 · D^2,67 i^0,5) + 0,1151] /0,631 = 0,64.

Так как наполнение превышает допустимое (табл. 5), увеличиваем диаметр на один размер по сортаменту D_ст = 0,3 м.

h/D = [0,025 /(56,1· 0,3^2,67 ·0,0039^0,5) + 0,1151] / 0,631 = 0,46.

Скорость V = 4 · Q/[π D² · (1,22 h/d – 0,1123)] = 0,79 м/с.

В соответствии с табл. 5 – скорость допустимая.

Пример.

На участке со значительным уклоном расход 0,65 м³/с. Требуется определить диаметр и уклон так, чтобы скорость не превышала допустимую V = 4 м/с.

Задаемся наполнением h/D = 0,7, скоростью V = 3,8 м/с, из формулы (13):

D = [4Q / (V · 3,14(1,22 h/D – 0,1123))]^0,5 =

= [4 ·0,65 /(3,8 ·3,14 (1,22 ·0,7- 0,1123))]^0,5 = 0,54 м.

Принимаем стандартный диаметр D = 0,6 м и из этой же формулы уточняем наполнение:

h/D = (4· Q / (3,14 ·V ·D²) + 0,1123)) / 1,22 =

= [4 · 0,65 /(3,14 · 3,8· 0,6²) + 0,1123)] /1,22 = 0,588.

Уклон из формулы (13)

i = [Q / (0,631 · h/D – 0,1151) · 56,1 · D^2,67)]² =

= [0,65/(0,62 · 0,56 – 0,11) · 56,1 ·0,6^2,67)]² = 0,0313.

При выполнении гидравлического расчета коллектора желательно, чтобы на каждом последующем участке скорость потока была больше скорости на предыдущем, это уменьшает возможность засорения сети.

Однако рельеф земли не всегда позволяет этого достичь. При переходе от большого уклона к малому скорость резко уменьшается. Если на верховом участке «а» поток наполнением h₁ «бурный» (величина наполнения меньше критической глубины H_кр), а на низовом участке поток глубиной h₂ «спокойный» (h₂ > H_кр) и при этом величина h₂ меньше сопряженной глубины h_с2 (h₂ < h_с2), произойдет отогнанный гидравлический прыжок, что может вызывать отложение взвешенных веществ на низовом участке «b».

Рис. 19. Гашение большой скорости на стыке участков

Если же h_с2 < h₂ (рис. 19), прыжок будет затоплен в пределах колодца.

Чтобы не допустить отогнанного прыжка, необходимо погасить скорость бурного потока в перепадном колодце, устраиваемом выше по течению от места стыка участков на расстоянии L = H_n /(i₁ – i₂), где H_n – величина перепада, принимаемая не менее D_b – диаметра на низовом потоке; i_a и i_b – уклоны соответственно на верховом и низовом потоках.

Критическая глубина определяется по формуле H_kp = D ∙ 0,5(1 – cos γ),

где величина γ вычисляется из уравнения:

D⁵ ∙ ( )³/ sin γ – 7,17q² = 0,

где q – расход, м³/с, D – диаметр верховой трубы.

Величину H_kp / D = 0,5 (1 – cos γ) можно найти из графика, где по оси ординат отложена величина 7,17 q² / D⁵.

Сопряженная с глубиной h₁ величина h_с2 [7].

h_с2 = 1,16· H_kp²/(h₁ + 0,16 · H_kp).

Пример.

Наполнение h₁ = 0,24 м, D = 0,4 м , q = 0,21 м³/с, V = 2,7 м/с, i = 0,026;

7,17 q²/D⁵ = 30,9; H _kp /D = 0,84; H_kp = 0,84 · 0,4 = 0,336 м; в верховой трубе h₁ < H_kp поток «бурный».

В низовой трубе h₂ = 0,36 м, D₂ = 0,6 м, q = 0,21 м³/с, V = 1,2 м/с,

i = 0,003;

7,17 q²/D⁵ = 4,07; H_kp /D = 0,46; H_kp = 0,46· 0,6 = 0,276 м.

h₂ > H_kp поток «спокойный».

При входе потока в нижележащую трубу со скоростью 2,7 м/с площадь живого сечения ω = q /V = 0,21/2,7 = 0,0778 м². Глубина потока в зависимости от площади и диаметра определяется по графику (рис. 21) или по формуле

h = 0,5 D (1 – cos γ),

где γ вычисляется из зависимости ω = 0,25 D² (γ – cos γ·sin γ);

ω/D² = 0,0778/0,6² = 0,216; по графику h/D = 0,31; h = 0,186 м.

7,17 q²/D⁵ = 4,07; H_kp = 0,276.

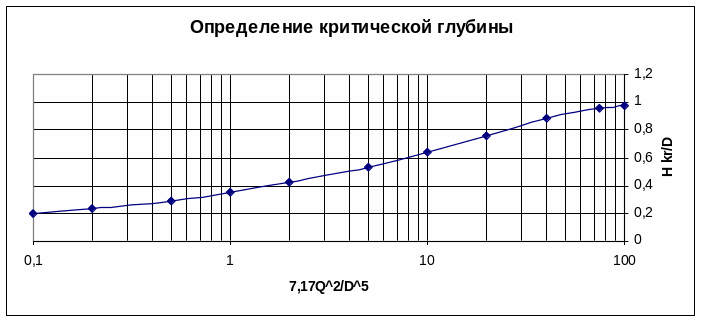
Рис. 20. Определение критической глубины

Сопряженная глубина h_c2 = 1,16 · 0,276² /(0,186 + 0,16 · 0,276) = 0,383 м. Так как h₂ < h_c2 появится отогнанный прыжок, требуется гашение скорости в перепадном колодце, устроенном на расстоянии L = 0,6/(0,026 – 0,003) = 26 м от места стыков участков.

Рис. 21. Определение наполнения