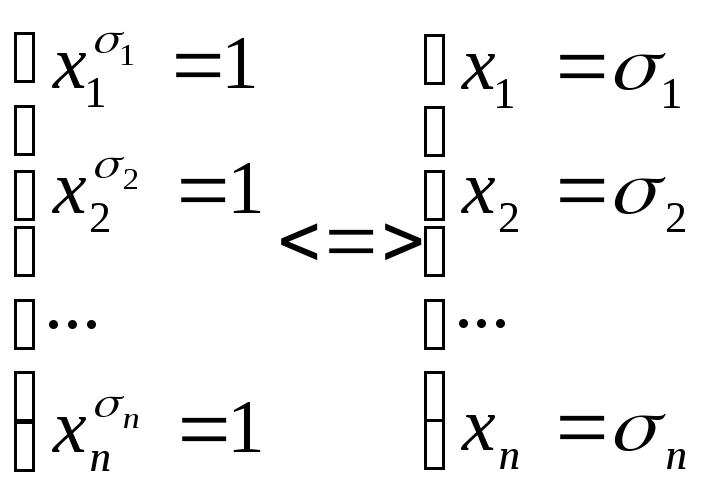Shpori_eshe

1. Множества. Операции над множествами. Булева алгебра множеств.

1.1 Булева алгебра множеств

Основными понятиями этой главы являются понятия множества и элемента множества (эти понятия считаем неопределяемыми). Синонимами слова множество являются слова совокупность, набор, коллектив и т.д. Множества мы будем обозначать большими буквами латинского алфавита (X, У, Z,...), элементы множества малыми буквами (х, у, z,...). При­надлежность элемента х множеству X (неопределяемое понятие) будем обозначать х X. Аналогично х X обозначает, что элемент х не принадлежит множеству X.

Определение 1.1. Множество X является подмножеством множества Y (обозначим

X Y), если для любого х X следует, что х Y.

Определение 1.2. Множества Х и Y равны (X = Y) тогда и только тогда, когда X Y и Y Х.

Будем считать, что мы выбрали некоторое достаточно большое множество, называемое универсальным, за пределы которого мы не будем выходить. Понятие универсального множества, обозначим его U также неопределяемое, но любое рассматриваемое нами мно­жество X удовлетворяет условию: X U. Это утверждение мы принимаем без дока­зательства. Заметим, что утверждения, которые считаются верными без доказательства, называются аксиомами.

Определим следующие операции над множествами:

объединением двух множеств Х и Y называется множество Х Y = {х U | х X или х Y}; пересечением двух множеств Х и Y называется множество Х ∩ Y = {х U| х X и х Y}; дополнением множества X называется множество = {х U | х X}.

Определение 1.3. Назовем пустым множеством (множеством, в котором нет ни одного элемента) множество Ø =, то есть дополнение к универсальному множеству.

Рисунки, интерпретирующие операции над множествами, называются диаграммами (кру­гами) Виенна.

Объединение Пересечение Дополнение

Теорема 1.4. Множества относительно операций дополнения, объединения и пересече­ния удовлетворяют следующим равенствам

1. = X - закон двойного отрицания;

2. XY = Y X - коммутативность;

3. X ∩ Y = Y ∩ X - коммутативность;

4. X (Y Z) = (X Y) Z - ассоциативность;

5. X ∩ (Y ∩ Z) = (X ∩ Y) ∩ Z - ассоциативность;

6. X (Y ∩ Z) = (X Y) ∩ (X Z) - дистрибутивность;

7. X∩ (Y Z) = (X ∩ Y) (X ∩ Z)- дистрибутивность;

8. = ∩ - закон де Моргана;

9. = - закон де Моргана;

10. XX = X- закон идемпотентности;

11. Х∩Х = Х- закон идемпотентности; законы нуля и единицы:

12. XU= U;

13. X∩U = X; 14. XØ = X;

15. X ∩Ø = Ø;

16. X (X∩Y) = X - закон поглощения;

17. X ∩ (XY) = X - законы поглощения;

18. X = U - законы дополнения;

19. Х ∩ = Ø - законы дополнения.

Все эти равенства следуют непосредственно из определения и демонстрируются с помо­щью кругов Виенна.

Множество с операциями, удовлетворяющими 19 приведенным выше равносильностям, называется булевой алгеброй; сами операции в этом случае называются булевыми. Из теоремы 1.4 следует, что множество всех множеств образует булеву алгебру относительно операций дополнения, объединения и пересечения. Заметим, что в дальнейшем мы будем рассматривать и другие множества, образующие булеву алгебру. Кроме булевых, над множествами определяются следующие операции.

3. Конечные множества. Правила суммы для конечных множеств.

Комбинаторика - это раздел математики, посвященный способам подсчета числа элемен­тов в конечном множестве. В этом параграфе все множества предполагаются конечными, то есть в них конечное число элементов. Будем обозначать |Х| число элементов множества X.

В качестве аксиом в комбинаторике принимаются следующие:

1. Отрезок натурального ряда {1,2,...,п} содержит п элементов.

2. Если существует биективное отображение φ: X → Y, то |Х| =|Y| .

3. |Ø| = 0.

Если |Х| = п, то элементы множества X можно пронумеровать, то есть определить биек­тивное отображение φ : {1,2,...,п}→ Х и обозначить φ(1) = х₁ φ(2) = х₂,..., φ(п) = х_п. Ясно, что нумерация не однозначна.

Теорема 1.19. Пусть X uY - конечные множества и X ∩ Y = Ø. Тогда |X Y| = |Х| + |Y|.

Доказательство. Действительно, если X = {х₁,х₂, ...,х_п}, Y = {у₁,у₂, ...,у_т}, то X Y =

{х₁, ...,х_п, у₁,..., у_т}. (Мы пронумеровали множества X и Y и воспользовались тем, что

x_i ≠ x_j для любых i{1,…,n}, j{1,…,m}.

Теорема 1.20 (Правило суммы). Пусть X u Y - конечные множества. Тогда |X Y| = |X| + |Y| - |X ∩ Y|

Доказательство. Очевидно, что X Y = X (Y \ X) и X ∩ (Y \ X) = Ø. Тогда |Х Y| = |X| + |Y \ X| по предыдущей теореме. Аналогично, |Y| = |Y \ Х| + |У ∩ Х|. Следовательно |Y \ X| = |Y| - |Y ∩ X| и |X Y| = |X| + |Y| - |X ∩ Y|. Теорема доказана.

Теорема 1.21. Пусть A₁,A₂,... ,А_п - конечные множества. Тогда

|A₁ A₂ . . . A_n| = |A₁| + |A₂| + . . . + |A_n| -

- (|A₁ ∩ A₂| + |A₂ ∩ A₃| + . . . + |A_n−1 ∩ A_n|)+

(|A₁ ∩ A₂ ∩ A₃| + . . . + |A_n−2 ∩ A_n−1 ∩ A_n|)+

. . . + (−1)ⁿ⁻¹ |A₁ ∩ A₂ ∩ . . . ∩ A_n| .

Теорема доказывается с помощью индукции и использования предыдущей теоремы.

Задача. В студенческой группе 25 человек. 14 студентов изучают английский язык, осталь­ные 16 студентов изучают немецкий язык. Сколько студентов изучают два языка: англий­ский и немецкий?

Решение. Обозначим через X множество студентов, изучающих английский язык, через Y - множество студентов, изучающих немецкий. Тогда |Х| = 14, |Y| = 16, |Х Y| = 25. Следовательно 25 = 14+16 - |Х∩Y| и количество студентов, изучающих два языка равно |Х∩Y| = 5.

4. Декартово произведение множеств. Количество элементов в декартовом произведении конечных множеств.

Определение 1.22. Декартовым произведением двух множеств X uY называется мно­жество пар (х,у) таких, что х X, у Y. Обозначим это множество X × Y.

Итак X × Y = {(х,у) | х X, у Y} . Равенство элементов в множестве X × Y понимается следующим образом: (x₁, y₁) = (x₂, y₂) тогда и только тогда, когда x₁ = х₂ и у₁ = у₂. Очевидно, что X × Y ≠ Y × X, если X ≠ У.

Определение 1.23. Декартовым произведением п множеств {Х₁,Х₂, ...,Х_п} называет­ся множество

X₁ × X₂ × ... × X_n = {(x₁,x₂,...,x_n) | x_i X_i Vi= 1,...,n} ,

то есть множество упорядоченных строк из п элементов.

Заметим, что множество X × X × ... × X обычно обозначают Х^п.

Теорема 1.24. Если X u Y - конечные множества, то X × Y - конечное множество и |Х × Y| = |Х| ∙ |Y|.

Доказательство. Зафиксируем в X нумерацию, то есть X = {х₁,х₂, ...,х_п}. Тогда

X × Y = × Y и (x_i × Y) (x_j × Y) = Ø, если i≠j.

По правилу суммы |Х × Y| =|x_i × Y|. Так как отображение f_i :x_i × Y →Y такое, что f_i((x_i, y)) = y, является биекцией для любого i (i=1,…,n), то |x_i × Y| = |Y| и |Х × Y| = |Х| ∙ |Y|.

Следствие. Если Х₁,Х₂, ...,Х_п - конечные множества, то |Х₁×Х₂×...×Х_п| = |Х₁|∙|Х₂|∙...∙|Х_п|

Задача. Из города А в город В ведет 3 дороги, из города В в город С - 4 дороги. Сколько различных дорог ведет из города А в город С ?

Решение.

Обозначим через X множество дорог из А в В, Y - множество дорог из В в С. Тогда X = {х₁,x₂,х_з} , Y = {y₁,y₂,y_з}. Каждая дорога из А в С является парой (x_i,y_j), где x_i X, y_j Y. Таким образом множество всех дорог из А в С является декартовым произведением X ×Y. Следовательно |Х × Y| = |Х| ∙ |Y| = 12.

6. Множество инъективных отображений: In Y^X и |In Y^X|.

7. Множество биективных отображений Bi Y^X и |Bi Y^X|

Определение 1.27. Пусть X и Y непустые множества. Отображение f : X → Y назы­вается иньективным, если из условия х₁ ≠ х₂ (х₁, х₂ - любые элементы множества X) следует, что f{x₁) ≠ f(x₂).

Множество всех инъективных отображений обозначим InY^X

Теорема 1.28. Пусть X uY - конечные непустые множества. Тогда l)InY^X ≠ Ø тогда и только тогда, когда |Y| > |Х|; 2) если |Х| = |Y|, то InY^X = BiY^X.

Доказательство. Пусть X = {x₁,x₂ ,…,х_т} и Y = {y₁,y₂ ,…,y_m}.

Докажем =>. Итак, InY^x ≠ Ø. Тогда существует инъективное отображение f : X → У.

Следовательно f(X) = {f(x₁), f(x₂),…, f(x_m)} Y и |f(Х)| = |Х| < |У|. Заметим, что мы использовали инъективность отображения f : f(x_i) ≠ f(x_j), если x_i ≠ x_j.

Пусть теперь п > т. Тогда мы можем построить такое отображение из множества X в множество Y: f(x_i) = у_i если i {1,2,...,m}. Так как f InY^X, то InY^X Ø.

2)Очевидно, что, если п = m, то любое инъективное отображение будет биективным.

Теорема 1.29. Пусть X ,Y - конечные непустые множества и |Y| > |Х|. Пусть |Х| = т, |Y| = п. Тогда

|InY^X| =n ∙ (п- 1) ∙ ... ∙ (п – т + 1)

Доказательство. Пусть X = {х₁,х₂,... ,х_т}, Y = {у1, y₂,,…, у_п}. Любое отображение f : X → Y определяется тем, куда попадет каждый элемент множества X, то есть на­бором элементов {f(x₁), f(x₂),..., f(x_m)} из множества Y. При этом отображения f и g различны, если f(x_i) ≠ g(x_i) хотя бы для одного i {1, 2,..., m}. Будем считать элементы множества Y ячейками.

Так как мы рассматриваем инъективные отображения множества X в множество Y, то два разных элемента множества X при любом отображении попадут в две разные ячейки. Задача о нахождении InY^X превращается в задачу о нахождении количества способов размещения элементов {х₁,х₂ ,..., х_т} по п различным ячейкам. Зафиксируем элемент х₁.

Существует п различных способов размещения этого элемента, так как он может попасть в любую из ячеек {y₁, у₂ ,...,у_п}. Предположим, что элемент х₁ в ячейку y_j. Тогда элемент x₂ может попасть при размещении в любую ячейку, за исключением у_j. Таким образом получаем п ∙ (п — 1) различных способов размещения элементов {х₁,x₂}. При размещении элементов {х₁, x₂, х₃} мы получаем п ∙ (п — 1) ∙ (п — 2) различных способа размещения, так как элемент x₃ можно разместить в любой из (п — 2) ячеек (две ячейки уже заняты элементами х₁ и x₂). Продолжая этот процесс, получаем, что число различных размещений т элементов по п ячейкам вычисляется по формуле: n ∙ (п- 1) ∙ ... ∙ (п – т + 1).

В комбинаторике это число обозначается и называется числом размещений длины т на множестве из п элементов (число ячеек). Итак, мы доказали, что |InY^X| = = n ∙ (п- 1) ∙ ... ∙ (п – т + 1) =n!/(n-m)!.

Следствие. Пусть X и Y такие множества, что |Х| = |Y|. Если обозначить BiY^X мно­жество всех биективных отображений из множества X в множество Y, то |BiY ^X| = n!

Доказательство. Действительно, если существует биективное отображение из множества X в множество Y, то |Х| = |У| = n |BiY ^X |= n!/(n-m)! = п!. Заметим, что в этом случае BiY^X = InY^X.

Каждое биективное отображение множества X = {х₁,х₂,..., х_п} в множество Y = {y₁,y₂,,…, у_п} является некоторым размещением элементов {x₁, x₂,..., х_п} по ячейкам {у₁, у₂,..., у_п}, то есть некоторой перестановкой элементов множества X. Число всех перестановок п раз­личных элементов обозначают Р_п, таким образом Р_п = п!.

Задача. В кабину лифта девятиэтажного дома вошли 4 пассажира. Сколько существует способов разгрузки лифта, если каждый пассажир может выйти на любом из 8 этажей, но при этом на любом этаже может выйти не более одного человека?

Решение. Пусть X - множество пассажиров, Y - множество этажей. Каждый способ разгрузки лифта в нашей задаче - это некоторое инъективное отображение множества X в множество Y: два разных пассажира обязательно выйдут на двух разных этажах. Следовательно число различных способов разгрузки лифта совпадает с числом различных инъективных отображений из множества X в множество Y и равно |InY^X|=8!/(8-4)!= 8∙7∙6∙5= 1680.

Задача. В аудитории 50 мест. Сколько существует способов размещения в аудитории 1) студенческой группы из 25 человек; 2) студенческого потока из 50 человек?

Решение. Пусть X - множество студентов, Y - множество мест в аудитории. Тогда в случае 1) количество различных способов размещения студентов в аудитории равно |InY^X| =50!/25!. В случае 2) количество различных способов размещения студентов в ауди­тории равно |BiY^X| = 50!.

Рассмотрим следующую задачу: сколькими способами из конечного множества X такого, что |Х| = п, можно выбрать m-элементные подмножества (m < п)?

Пусть X = {х₁,х₂,..., х_п}. Рассмотрим множество Т = {1,2,..., m} и множество всех инъективных отображений из Т в X. Количество таких отображений равно |InY^X| = n!/(n-m)!. Заметим, что каждое инъективное отображение f : Т → X выделяет некоторое под­множество множества X. А именно, если f(j) = x_ij при j Т, то X_f = {х_i1, х_i2,..., х_im} - выделенное подмножество. С другой стороны по каждому подмножеству А = {х_j1, х_j2,..., х_jm} можно построить отображение f : Т → X такое, что f(k) = x_jk для к Т. Будет ли число различных m-элементных подмножеств множества X совпадать с |InY^X|? Ответ на этот вопрос отрицательный. Действительно, подмножество Х_о = {х_i1, х_i2,..., х_im} совпадает с подмножеством Х₁ = {х_i2, х_i3,..., х_im, x_i1}, однако fx₀ ≠ fx₁. Количество различных инъективных отображений, соответствующих подмножеству Х_о, совпадает с числом раз­личных перестановок элементов множества Х_о и равно га!. Заметим, что это утверждение верно для любого m-элементного подмножества множества X. Таким образом, получаем, что число различных m-элементных подмножеств множества X равно

Очевидно, что имеют место следующие равенства:

1)Х\Ø = Х; 2) X\U = Ø; 3) Ø\Х = Ø; 4)Х\Х= Ø;5)U\X = ; 6) X ΔY = Y Δ Х;

7) X Δ U = ; 8) X \ Ø = X

Рассмотрим более подробно свойства подмножеств данного множества.

Теорема 1.7. Пусть X и Y - множества. Тогда X Y тогда и только тогда, когда X\Y = Ø

Теорема 1.8. Пусть X, Y, Z - множества. Тогда:

1. X X - рефлексивность;

2. из (X Y) и (Y Z) следует X Z - транзитивность;

3. из (X Y) и (Y X) следует X = Y - антисимметричность.

Доказательства приведенных выше теорем следуют непосредственно из определений. Замечание: понятия коммутативности, ассоциативности, дистрибутивности, рефлексивно­сти, транзитивности и антисимметричности будут подробно рассмотрены в последующих главах этой книги.

2. Отображения множеств. Типы отображений. Композиция. Обратимость отображений.

Определение 1.9. Пусть X и Y - множества. Отображением f из множества X в множество Y мы будем называть правило, по которому каждому элементу х множе­ства X ставится в соответствие вполне определенный (единственный) элемент y = f(x) множества Y. Обозначать данное отображение будем f: X → Y.

Заметим, что отображение надо обязательно понимать как набор из трех элементов (X, Y, f), где X и Y - множества, f - закон.

Определение 1.10. Пусть f: X → Y - отображение, А X, В У. Тогда:

1) образом множества А при отображении f называется множество f(A)= {f(x ) | xA};

2) прообразом множества В при отображении f называется множество f ^-1 (B) = {xX | f(x) B}.

Теорема 1.11. Пусть f : X → Y - отображение; А₁, А₂ X; B_1; B₂ Y. Тогда:

1) f(A₁ A₂) = f(A₁) f(A₂); 2) f ⁻¹(B₁ B₂) = f ⁻¹(B₁) f ⁻¹(B₂);

3) f(A₁ ∩ A₂) f(A₁) ∩ f(A₂); 4) f ⁻¹(B₁ ∩ B₂) = f ⁻¹(B₁) ∩ f ⁻¹(B₂).

Доказательство. Приведем доказательство утверждений 1) и 3), утверждения 2) и 4) доказываются аналогично 1). Итак, пусть у f(A₁ А₂). Это равносильно тому, что су­ществует х А₁ А₂ такой, что f(x) = у, то есть или существует х А₁ или существует х А₂ с условием у = f(x). Но это равносильно тому, что или у f(A₁) или у f(A₂), то есть у f(A₁) f(A₂). Первое утверждение теоремы доказано. Пусть теперь х - произволь­ ный элемент множества А₁ ∩ А₂. Тогда элемент х одновременно принадлежит множествам А₁ и А₂, и следовательно элемент f(x) одновременно принадлежит множествам f(A₁) и f(A₂), но по определению это и означает, что f(x) f(A₁) ∩ f(A₂). Таким образом дока­зали 3), то есть f(A₁ ∩ А₂) f(A₁) ∩ f(A₂). Обратное включение в общем случае неверно, что показывает следующий пример.

Пример. Пусть f: R→R такое отображение, что f(x) = sin x; A₁ = [0,π], А₂ = [2π,3π]. Тогда

А₁ ∩ А₂ = Ø, следовательно и f(A₁ ∩ А₂) = Ø но f(F₁) ∩ f(А₂) = [0,1] Ø.

Определение 1.12. Отображение f : X → Y называется инъективным, если для любых x₁ ≠ x₂ из множества X следует, что f(x₁) ≠ f(x₂).

Определение 1.13. Отображение f : X → Y называется сюрьективным, если для любо­го элемента у из множества Y существует непустой прообраз, то есть f ^-1(y )≠ Ø

Определение 1.14. Отображение f : X → Y называется биективным, если оно инъективно и сюръективно.

Примеры.

Отображение f : R → {0,1} такое, что f(n) = (1+(-1)ⁿ)/2 является сюръективным, но не инъективным. Заметим, что множество {0,1} обычно обозначают Е₂.

1. Отображение f : R → R такое, что f(x) = х² не является ни инъективным, ни сюръективным.

2. Отображение f : N → N такое, что f(n) = п² является инъективным, но не сюръективным.

3. Отображение f : R → R такое, что f(x) = х³ является биективным отображением.

Определение 1.15. Пусть f : X → Y, g : Y → Z - отображения, тогда композицией этих отображений называется отображение g о f : X → Z такое, что для любого элемента х из множества X его образ в множестве Z определен следующим образом (g o f)(x) = g(f(x)).

Теорема 1.16 (ассоциативность композиции отображений). Если f : X → Y, g : Y → Z,

h : Z → V — отображения, то справедливо следующее равенство: h о (g о f) = (h о g) о f.

Доказательство. Действительно, для любого х X справедливо:

(h o (g o f))(x) = h((g о f)(x)) = h(g(f(x))), ((h о g) о f)(x) = (h о g)(f(x)) = h(g(f(x))).

Определение 1.17. Тождественным отображением множества X на себя называется отображение e_X : X →X такое, что для любого х из множества X выполняется равенство e_X(x) = х.

Теорема 1.18. Если f : X →Y - биективное отображение, то существует такое биективное отображение g : Y→X, что:

1) для любого элемента х из множества X вып-ся равенство х = (д о f)(x), то есть g о f = е_Х,

2)для любого элемента у из множества Y вып-ся равенство у = (f о д)(у), то есть f о g = е_Y,

Отображение g в этом случае называют обратным отображением к отображению f и обо­значают f ^-1.

Доказательство. Искомое отображение f : Y → X определим следующим образом: g(у) = х, где х прообраз элемента у в множестве X. Этот прообраз существует и единстве­нен для любого элемента у из множества Y, так как отображение f - биективно. Таким образом отображение g определено, и биективность его очевидна. Из определения отображения g получаем 1) g(f(x)) = х. Аналогично выполняется 2) (f оg)(у)= f(g(y))= f(x) = y

5. Множество Y^X, и количество элементов |Y^X| в этом множестве.

Определение 1.25. Пусть X и Y - непустые множества. Множество всех отображений из X в Y назовем множество степень и обозначим Y^X, то есть Y^X = {f | f : X → Y} .

Теорема 1.26. Пусть X uY - конечные непустые множества. Тогда |Y^X| = |Y|^|X|.

Доказательство. Для доказательства теоремы применим индукцию по количеству элементов в множестве X. Пусть |Х| = 1, то есть X = {х}, Y = {y₁,y₂,…,y_m}. Каждое отображение f : X → Y определяется тем, куда попадет элемент х. В этом случае все раз­личные отображения из множества X в множество Y можно просто перечислить: f₁ - такое отображение, что f₁(x) = y₁; f₂ - такое, что f₂ (x) = у₂; ...; f_m - такое, что f_m(x) = у_m. Ясно, что все эти отображения разные и |Y^X| = m¹ = |Y|^|X|. Предположим далее, что для любого множества X такого, что |Х| < п. Пусть теперь |Х| = п, то есть X = {x₁,x₂ ,…,x_n}. Множество Y^X разобьем на непересекающиеся подмножества: Y^X = A₁ A₂ ... A_m, где m = |Y|, Y = {y₁, y₂,…,y_m}. A_j = {f : X → Y | f(x₁) = y_j }. Ясно, число A_j ∩ A_k = Ø, если j ≠ k. По правилу суммы |Y^X| = |А₁| + |А₂| + ... + |А_т|. Посчитаем теперь количество элементов в каждом множестве A_j. При любом отображении f Aj образ элемента х₁ фиксирован (f(x₁) = y_j), следовательно отображение f определя­ется только тем, куда попадут элементы множества Х \ {x₁}. Таким образом отображение f однозначно определяется своим ограничением на Х \ {х₁}, поэтому для любого j количе­ство элементов в множестве A_j совпадает с количеством всех различных отображений из множества Х \ {х₁} в множество Y. По предположению индукции |A_j| = |Y ^X\{x1}| = mⁿ⁻¹.

Тогда |Y ^X| = m · mⁿ⁻¹ = mⁿ = |Y |^|X|, что и требовалось доказать.

Задача. В кабину лифта девятиэтажного дома вошли 4 пассажира, каждый из которых может выйти на любом из 8 этажей. Сколько существует способов разгрузки лифта?

Решение. Обозначим через X множество пассажиров, через Y - множество этажей, на которых они могут выйти. Тогда каждая разгрузка лифта - это некоторое отображение f : X —> Y (каждому пассажиру поставлен в соответствие этаж, на котором он выходит при этой разгрузке). Следовательно число различных способов разгрузки лифта совпадает с числом различных отображений из множества X в множество Y, то есть равно |Y^X| = 8⁴ = 4096.

Задача. Пусть X - конечное множество. Найти количество всех различных подмножеств множества X.

Решение. Пусть Е₂ = {0,1}. Для любого подмножества А X определим отображение

f_A : X —> Е₂ следующим образом: f_A(х) = 1, если х A; f_A(х) = 0, если х А. Заме­тим, что множество всех таких отображений совпадает с множеством Е₂^X. Действительно, очевидно, что { f_A | А X} Е₂^X. С другой стороны, если f : X → Е₂ - произволь­ное отображение, то f = f_A, где А = {х X | f(x) = 1}. Очевидно, что отображение φ: {А | А X} → Е₂^X такое, что φ(А) = f_A, является биекцией. Следовательно количе­ство всех различных подмножеств множества X равно |Е₂^X| = 2^|X|.

Заметим,что множество всех подмножеств множества X обозначают 2_Xl и мы доказали, что

|2^Х| = 2^|X|.

8. Число сочетаний из n элементов по m элементам (C_n^m)

Число различных m-элементных подмножеств множества, состоящего из п элементов, называют числом сочетаний длины т из п элементов и обозначают . Итак, = n!/(m!(n-m)!) - число различных m-элементных подмножеств множества, состоящего из п эле­ментов.

Следствие. Пусть |Х| = п. Тогда число всех различных подмножеств множества X равно

Задача. В группе 25 человек. Сколько существует способов выбора из них делегации из трех человек для участия в профсоюзной конференции?

Решение. Ясно, что выбор делегации - это выбор 3-элементного подмножества из мно­жества студентов группы. Поэтому число способов выбора равно = 25!/(3!∙22!)= 2300.

Задача. В кондитерской продаются пирожные пяти видов: бисквитные, корзиночки, песочные, эклеры, трубочки. Сколькими способами можно купить 12 пирожных?

Решение. Каждая покупка однозначно определяется набором неотрицательных чисел {x₁, x₂, x₃, x₄, x₅}, где x_i - число покупаемых пирожных i-ого вида. Тогда наша задача равносильна задаче о числе решений уравнения x₁ + x₂ + x₃ + x₄ + x₅ = 12 при условии, что x_i Z,x_i > 0 для i {1,2,3,4,5}. Сделаем замену x_i + 1 = n_i. В результате получили задачу, равносильную первоначальной, о нахождении числа решений уравнения n₁+n₂ + n₃ + n₄ + n₅ = 17,

где для любого i число n_i N. Нарисуем прямую и отметим на ней 17 точек. Каждому решению нашего уравнения сопоставим картинку, состоящую из точек и черточек, кото­рая строится следующим образом. Если (,,,,) - решение, то отсчитаем слева направо отмеченных точек и за последней из них поставим черту. Затем отсчитаем точек и за последней из них также поставим черту, и так далее. Договоримся последнюю черточку не рисовать. Например, решению (2, 1, 4, 6, 4) соответствует рисунок

• • | • | • • • • | • • • • • • | • • • •

Ясно, что соответствие между решениями и картинками - биективное. Но каждая картин­ка определяется выбором 4-х промежутков, где ставится черта, из имеющихся 16. В нашем примере по решению (2, 1, 4, 6, 4) мы выбрали 4-элементное подмножество промежутков {2, 3, 7, 13}. Число способов выбора 4-элементных подмножеств множества, состоящего из 16 элементов, равно = 16!/(4!∙12!) = 1820

Задачи, сводящиеся к нахождению числа решений уравнения x₁ + x₂ + . . . + x_m = n, x_i Z, x_i ≥ 0Vi называют задачами на сочетания с повторениями длины п из т видов.

Теорема 1.30. Число сочетаний с повторениями длины п из т видов равно . При доказательстве используется та же схема, что и при решении предыдущей задачи.

11. Кольца. Поля. Определение и примеры.

12. Кольцо Z_m и кольцо Z_p.

Определение 2.13. Алгебраическая система (К, +, ∙) с двумя бинарными операциями, сложением и умножением, называется кольцом, если:

1. (К, +) - абелева группа;

2. {К,∙) - полугруппа;

3. операция умножения дистрибутивна относительно операции сложения, то есть:

а ∙ (b + с) = а ∙ b + а ∙ с, (b + с) ∙ а = b ∙ а + с ∙ а, Vа, b,с К.

Если в кольце К есть 1 по умножению так, что а ∙ 1 = 1 ∙ а = а для любого элемента а из К, то К называют кольцом с единицей; если операция умножения в кольце К - коммутативна, то есть а∙b = b∙ а для любых элементов а и b из К, то кольцо К называют коммутативным.

Примеры.

1. Алгебраические системы (Z, +, ∙), (Q, +, ∙), (Е, +, ∙) являются коммутативными кольца­ми с единицей.

2. Алгебраические системы (Mat_n×n(Z), +, ∙), (Mat_n×n(Q),+,∙), (Mat_n×n(R), +, ∙) являются кольцами с 1, но не являются коммутативными кольцами. ( Mat_n×n(P) - это множество матриц размера п × п над Р).

3)Пусть п - натуральное число. На множестве Z определим отношение эквивалентности:

z₁ ~ z₂ тогда и только тогда, когда z₁ — z₂ = п ∙ z для некоторого z Z.

Тогда множество Z разобьется на непересекающиеся классы эквивалентности:

Z = nZ (1 + nZ) ... ((n - 1) + nZ), (m + nZ = {m + nz | z Z}.)

Класс эквивалентности m + nZ обозначим для т {0,1,... ,п — 1}, то есть = m + nZ. Кольцом классов вычетов по модулю п назовем множество Z_n={,,...,}co следующими операциями сложения и умножения:

Заметим, что операции заданы корректно, так как для любого числа к Z найдется такое число т {0,1,..., п — 1}, что k = nq + m, q Z, следовательно k + nZ = т + nZ = т. Кольцо Z_n - это коммутативное кольцо с единицей. Нулем в этом кольце будет элемент , а единицей – эл. .

Определение 2.14. 1) Элемент к ≠ 0 в кольце К называется делителем 0, если в кольце К найдется такой элемент b ≠ 0, что b∙k = 0 или k∙b = 0. 2) Элемент k ≠ 0 в кольце К называется нильпотентным, если k^п = 0 для некоторого n N.

Примеры.

1. В кольце Z₆ элементы и являются делителями 0, так как .

2. В кольце Z₄ элемент является нильпотентным элементом и делителем 0, так как .

Заметим, что в кольце с единицей делители нуля и нильпотентные элементы не могут быть обратимыми.

Определение 2.15. Ненулевое коммутативное кольцо Р с единицей называется полем, если любой его ненулевой элемент - обратим.

Примеры.

1. (Q, +, ∙) - поле рациональных чисел.

2. (R, +, ∙) - поле действительных чисел.

3. (С, +, ∙) - поле комплексных чисел.

4. (Z₂, +, ∙) - поле классов вычетов по модулю 2.

Обобщим последний пример.

Теорема 2.16. Кольцо Z_n будет полем тогда и только тогда, когда п - простое число.

Доказательство. => Пусть Z_n - поле и п = k∙т, где k,т N, k, т ≠ 1, n. Тогда и элемент k не может быть обратим. Действительно, предположив, что существует элемент такой, что, получим

,

то есть и т = п. Итак, если п - составное число, п = k∙т, то элемент - необратим, что противоречит условию: Z_n - поле.

<= Пусть р - простое число. Докажем, что Z_p - поле. Так как известно, что Z_p - комму­тативное кольцо с единицей, достаточно доказать, что любой ненулевой элемент в Z_p -обратим. Пусть - произвольный элемент из Z_p. Так как т < р и р - простое чис­ло, то натуральные числа тир- взаимно просты. Тогда, используя алгоритм Евклида, можно найти такие числа a ,b N, что а ∙ т + b∙ р = 1. Следовательно

и элемент т - обратим. Заметим, что единичный элемент всегда обратим.

Без доказательства сформулируем следующую теорему.

Теорема 2.17. Пусть 1 и 0 - единица и нуль поля Р. Тогда либо п ∙ 1 ≠ 0 для любого натурального числа п, либо существует простое натуральное число р такое, что р ∙ 1 = 0. Впервом случае говорят, что поле Р имеет нулевую характеристику и пишут charP = 0; во втором случае, говорят, что поле Р имеет характеристику р и пишут charP = p, в этом случае аддитивная группа, или группа по сложению, порожденная элементом 1, изоморфна полю Z_p и состоит из элементов k ∙ 1, k {0,1,... ,р — 1}.

9. Множество с операциями. Алгебраические структуры. Полугруппа. Моноид. Группа. Определение и примеры.

10. Группа подстановок.

Определение 2.1. Бинарной операцией на множестве X называется правило, по кото­рому любым двум элементам x, y из множества X ставится в соответствие некоторый, однозначно определенный, элемент из X, обозначаемый х * у.

Заметим, что на множестве X могут быть определены и так называемые унарные опе­рации: каждому элементу множества X ставится в соответствие некоторый, однозначно определенный, элемент множества X. Таким образом задание унарной операции - это задание некоторого отображения f : X —> X. Точно также на множестве определяют­ся нуль-арные операции: выделение какого-то элемента множества. По аналогии можно определить п-арную операцию на множестве X как некоторое отображение f : Х^п → X.

На одном и том же множестве могут быть определены несколько операций. Например, на множестве Z определены две бинарные операции: сложение и умножение; унарная операция: каждому элементу z множества Z ставится в соответствие элемент (—z); две нуль-арные операции: выделение 0 и 1.

Определение 2.2. Операция * на множестве X называется

1) ассоциативной, если для любых элементов х, у, z X выполняется равенство (x*y)*z=х* (y*z);

2)коммутативной, если для любых элементов х,у X выполняется равенство х*у = у*х.

Определение 2.3. Элемент e в множестве X называется нейтральным, единицей, от­носительно операции * на X, если для любого элемента х из множества X выполняется равенство х*е=е*х= х.

Заметим, что выделение нейтрального элемента в множестве задает нуль-арную операцию на этом множестве. Если операция * - обычное умножение на множестве N, Z или R, то е = 1 называют единицей; если же * - обычное сложение, то е = 0 называют нулем.

Примеры.

1) Бинарные операции сложения и умножения на множестве Z - ассоциативны и комму­тативны. Нейтральным эл-ом относительно операции сложения яв-ся 0, а относи­тельно умножения – 1.

2) Рассмотрим множество матриц порядка 2×2 (таблица, состоящая из действительных чисел), такое множество обычно обозначают M₂(R). На этом множестве определены две бинарные операции: сложение и умножение. Операция сложения - ассоциативна и комму­тативна; операция умножения - ассоциативна, но не коммутативна. Нейтральным элемен­том относительно сложения является матрица

Определение 2.4. Непустое множество X с заданной на нем ассоциативной операцией *, обозначаем (X, *), называется полугруппой. Полугруппу (X, *), в которой относительно операции * существует нейтральный элемент, называют моноидом.

Пример. Рассмотрим набор букв (алфавит) и множество слов в этом алфавите, которое обозначим М. На множестве М зададим бинарную операцию * следующим образом: для любых слов u иvиз мн-ва М определим и * v = uv, то есть слово и * v получено приписыванием к слову и слова v. Тогда (М, *) - полугруппа. Доб. к мн-ву М пустое слово е, тогда ({М, е}, *) - моноид.

Теорема 2.5. Нейтральный элемент в моноиде - единственен.

Доказательство. Пусть (М, *) - моноид; е, f - два нейтральных элемента в (М, *). Тогда е = е*f = f по определению.

Определение 2.6. Пусть (М, *, е) - моноид. Элемент b называется обратным к элементу а, если а*b=b*а=е. Элемент а в этом случае называют обратимым элементом; элемент b обозначают а ^-1.

Заметим, что, если * - операция сложения, то вместо а ^-1 пишут — а и называют этот элемент противоположным к элементу а. Например, в моноиде (Z, +,0) любой элемент z имеет противоположный элемент — z, то есть на множестве Z определена унарная опера­ция: f(z) = —z. В моноиде (Z, ∙, 1) обратимы только два элемента: 1 и -1.

Теорема 2.7. Пусть (М, *,е) - моноид. Тогда:

1. для любого элемента а М обратный элемент, если он существует, - единственен;

2. элемент е - обратим и е ^-1 = е;

3. обратный элемент a ^-1 к элементу а, если он существует, обратим и (а ^-1) ^-1 = а;

4. если а, b - обратимые элементы в М, то (а * b) ^-1 = b ^-1 * a ^-1.

Доказательство. 1) Предположим b₁, b₂ - обратные элементы к элементу а М. Тогда

b₁ = b₁ * e = b₁ * (a * b₂) = (b₁ * a) * b₂ = e * b₂ = b₂.

Утверждения 2) и 3) - очевидны.

4) Так как (а * b) * (b ^-1 * а ^-1) = а * (b * (b ^-1 * b ^-1)) = а * ((b * b ^-1) * a ^-1) = а * (е * a ^-1) = а * a ^-1 = е, то 4) доказано.

Определение 2.8. Алгебраической системой называют непустое множество с семейством операций и отношений, заданных на нем.

Мы уже рассматривали примеры алгебраических систем: полугруппы, моноиды, линейно или частично упорядоченные множества, множества с отношением эквивалентности. Пример более богатой структуры: (Z, +, ∙, 0,1, ≤).Здесь определены две бинарные операции: + и ∙ ; две 0-арные операции: выделены 0 и 1 ; определено также отношение порядка ≤

Рассмотрим три основных способа построения новых алгебраических из уже имеющихся.

Определение 2.9. Пусть М - алгебраическая система, N является подмножеством мно­жества М, N ≠ Ø. N называется подсистемой алгебраической системы М, если

1. N замкнута относительно всех операций, определенных на N: для любой n-арной опера­ции f(a₁,..., а_п), определенной на множестве М, и любого набора элементов {m₁,..., т_п} из множества N элемент f(m₁,..., т_п) N;

2. для любого отношения S, заданного на множестве М в данной алгебраической системе, определено сужение S_N этого отношения на подмножестве N: если n₁, n₂ N, то n₁ S_N n₂ тогда и только тогда, когда n₁ S_n2

Заметим, что, если алгебраическая система имеет специальное название: моноид, группа, кольцо, поле, то подсистема называется соответственно: подмоноид, подгруппа, подкольцо, подполе.

13. Отношения на множестве. Отношения порядка. Определение и примеры.

14. Отношение эквивалентности. Определение и примеры.

Определение 1.31. Пусть {X₁, X₂,... ,Х_п} - непустые множества. Тогда п-местным отношением, заданным на декартовом произведении Х₁ × Х₂ × ... × Х_п, называют под­множество S Х₁ × Х₂ × ... × Х_п,. При этом, если (х₁,₂,..., х_п) S, то говорят, что элементы {х₁, x₂,..., х_п} множества X связаны отношением S; если же (х₁,₂,..., х_п) S то говорят, что элементы {х₁, x₂ ,..., х_п} не связаны отношением S.

Примеры.

1) На декартовой плоскости R² = R × R рассмотрим подмножество S - прямую, являющуюся биссектрисой первой и третьей четверти. Ясно, что пара чисел {х₁,х₂} из R связана двуместным отношением S тогда и только тогда, когда (х₁,х₂) S,to есть х₁ = х₂.

Рисунок.

2) Рассмотрим 3-местное отношение на R³, заданное следующим образом: (х₁,х₂,x₃) тогда и только тогда, когда = x₃. Ясно, что в этом случае подмножество S –параболоид вращения.

Рисунок.

Двуместные отношения называют бинарными. Для бинарных отношений вместо записи (х,у) S принята запись хαу: элементы х и у находятся в отношении α. За наибо­лее распространенными бинарными отношениями закреплены специальные обозначения: {=,≤,<,>,≥,С,~}.

Определение 1.32. Пусть α - бинарное отношение на X × Y, β - бинарное отношение на Y × Z. Тогда композицией отнтшенип α и β называется бинарное отношение, обозна­чаемое α о β, на X × Z, определенное следующим образом: х(а о β)y тогда и только тогда, когда существует такой элемент у Y, что хαу и yβz.

Для композиции отношений выполняется свойство ассоциативности, то есть (α о β) о γ = α о (β о γ) для любых бинарных отношений α, β,γ - Заметим, однако, что для произвольных бинарных отношений α и β не выполняется коммутативность то есть α о β ≠ β о α.

Определение 1.33. Бинарным отношением на множестве X называется бинарное от­ношение на X × X.

Примеры.

1)Пусть X = R. Тогда на этом множестве можно определить следующее бинарное отно­шение α: хαу тогда и только тогда, когда х² = у² (х и у - элементы множества R.)

2) Пусть X = N. Тогда на множестве N определим следующем образом бинарное отноше­ние <:

п₁ ≤ n₂ тогда и только тогда, когда (n₂ — n₁) N {0} .

3) Пусть X = N. Тогда на множестве N определим следующем образом бинарное отноше­ние <:

п₁ < п₂ тогда и только тогда, когда (п₂ — п₁) N.

Далее сформулируем определения основных свойств бинарных отношений: рефлексив­ности, транзитивности, симметричности и антисимметричности. С помощью этих свойств выделяются два важнейших вида бинарных отношений: отношение порядка и отношение эквивалентности.

Определение 1.34. Бинарное отношение α на множестве X называется рефлексивным, если для любого элемента х из множества X выполняется отношение хαх.

Определение 1.35. Бинарное отношение α на множестве X называется транзитивным, если для любых элементов х, у, z из множества X таких, что хαу и yαz, следует, что xαz.

Определение 1.36. Бинарное отношение α называется симметричным, если для любых элементов x, у из множества X таких, что хαу, следует, что уαх.

Определение 1.37. Бинарное отношение α на множестве X называется антисиммет­ричным, если для любых элементов х, у из множества X таких, что хαу и уαх, следует, что x = у.

Примеры.

1. Отношение = на любом множестве X является рефлексивным, транзитивным и симметричным.

2. Отношение ≤ на множестве N является рефлексивным, транзитивным и антисимметричным.

3. Отношение < на множестве N является транзитивным, но не является рефлексивным, симметричным и антисимметричным.

4. Пусть X - произвольное непустое множество. Тогда на множестве 2^X (множество всех подмножеств множества X) рассмотрим бинарное отношение (Х₁ Х₂). Это бинарное отношение будет рефлексивным, транзитивным и антисимметричным.

Определение 1.38. Бинарное отношение α на множестве X называется отношением по­рядка, если оно рефлексивно, транзитивно и антисимметрично. При этом, если для любых элементов х, у из множества X справедливо либо хαу, либо уαх, то α называют линейным порядком, а пару (X, α) (множество X с линейным порядком α) - линейно упорядоченным множеством; в противном случае α - частичный порядок, а (Х,α) - частично упорядо­ченное множество.

Примеры.

1. (N, ≤), (R, ≤) - линейно упорядоченные множества.

2. {2^А, ) - частично упорядоченное множество, если |А| > 1. Если же |А| = 1, то (2^A, ) - линейно упорядоченное множество.

Определение 1.39. Бинарное отношение α на множестве X называется отношением эквивалентности, если оно рефлексивно, транзитивно и симметрично.

Примеры.

1. Отношение α на множестве R такое, что хαу тогда и только тогда, когда х² = у², является отношением эквивалентности.

2. Отношение = на N, R и на любом множестве X является отношением эквивалентности.

Определение 1.40. Пусть α - отношение эквивалентности на множестве X, х - произ­вольный элемент множества X. Тогда классом эквивалентности (смежности) элемента х по отношению эквивалентности α называется множество [х]_α = {у X | хαу}.

15. Определение графа. Виды графов. Подграфы. Операции над графами.

16 . Изоморфизм. Помеченные и непомеченные графы. Матрицы, ассоциативные с помеченными графами.

Определение графа

Пусть задано конечное множество V , которое будем называть мно­жеством вершин. Некоторые из этих вершин соединим ребрами, т.е. выделим в множестве V⁽²⁾ всех двухэлементных подмножеств множе­ства V некоторое подмножество Е, которое и будем называть множе­ством ребер графа. Итак, граф - это пара (V, Е), где V - конечное множество, а Е V⁽²⁾. Более подробно множества V и Е обознача­ются как VG и EG соответственно. Число card(VG) вершин графа G называют его порядком и обозначают через |G|.

Говорят, что две вершины u и v смежны, если множество {u,v} явля­ется ребром, и не смежны в противном случае. Если е = {u,v} - ребро, то вершины и и v называют его концами и говорят, что ребро е со­единяет вершины u и v, Такое ребро обозначается символом uv. Два ребра называются смежными, если они имеют общий конец. Вершина о и ребро е называются инцидентными, если и является концом ребра е (т.е. е = uv) и не инцидентными в противном случае.

Множество всех вершин графа G, смежных с некоторой вершиной v, называется окружением вершины v и обозначается через N_G(v) или N(v).

Рис.1

Графы удобно изображать в виде рисунков, состоящих из точек (вер­шины графа) и линий, соединяющих некоторые из этих точек (ребра графа). Приведем примеры некоторых графов специального вида. Граф G называется полным, если любые две его вершины смежны, т.е. EG = (VG)⁽²⁾. Полный граф порядка п обозначим К_п, число ребер в нем рав­но С_n² = п(п — 1)/2. На рис.1, а изображен полный граф К₅. Граф называется пустым , если в нем нет ребер. Пустой граф порядка п обозначим О_n. На рис.1 б,в показаны также простые циклы С_п для n = 3,4 , а на рис.1 г, д - простые цепи Р_п для п = 4,5. Очевидно, что К₂ = Р₂ и К₃ = С₃.

Рис.2

На рис.2, а,б приведены два изображения простого цикла С₅ , а также колее W_n для п = 3,4 (в,г).

Красивыми примерами являются графы пяти платановых тел (т.е. правильных многогранников): тетраэдра, куба, октаэдра, додекаэдра, икосаэдра.

Напомним, что разбиением множества S называется представление его в виде объединения подмножеств, никакие два из которых не пе­ресекаются. Граф называется двудольным, если существует разбиение множества его вершин на части (доли) такие, что концы каждого ре­бра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф, доли которого состоят из р и q вершин, обозначается символом K_p,q . При р = 1 получаем звезду К_1,q. Легко проверить, что K_1,1 = К₂ = P₂ , K_1,2 = Р₃. На рис. 3 изображены звезда K_1,5 и двудольный граф K_3,3. Как видно из определения, граф - это алгебраическая система с одним отношением специального вида. Следовательно, к графам применимы понятия гомоморфизма, изоморфизма и автоморфизма. В част­ности, два графа G и Н называются изоморфными, если существует биекция φ: VG → VH такая, что две вершины u,v VG соединены ребром тогда и только тогда, когда их образы φ(и), φ(v) соединены ребром в H. В этом случае пишем GH, Например, граф К_3,3 на рис.3 изоморфен графу "а" на рис.4, а графы "б" и "в" на этом же рис. 4 не изоморфны. В некоторых ситуациях все же приходится различать изоморфные графы, и тогда полезно понятие помеченного графа. Граф порядка п называется помеченным, если его вершинам присвоены не­которые метки, например, номера 1,2,... , п. Отождествим каждую из вершин графа с ее номером и определим равенство помеченных гра­фов G и Н одного и того же порядка: G = Н тогда, когда EG = EH. Различные помеченные графы могут быть изоморфны между собой.

Для произвольного графа G определяется дополнительный граф : множество вершин у него то же самое, что и у графа G, a E= V⁽²⁾ \ EG, т.е. две вершины в смежны тогда и только тогда, когда они не являются смежными в G. Граф, изоморфный своему дополнению, называется самодополнительным. Например, K₁,P₄,C₅ - самодополни­тельные графы.

Иногда приведенное выше определение графа недостаточно и при­ходится рассматривать более общие объекты, в которых две вершины могут быть соединены более чем одним ребром. Так возникает понятие "мультиграф". Дальнейшее обобщение состоит в том, что кроме крат­ных ребер допускаются еще и петли, т.е. ребра, соединяющие вершину саму с собой. Такой объект называется псевдографом. Изучаются так­же ориентируемые графы: это пара, состоящая из множества вершин V и из нек. подмнож. А декартова квадрата V² (вместо V⁽²⁾), Если а = (u,v) А, то а изобр. дугой со стрелкой; и назыв. началом, а v - концом этой дуги.

Определение 2.10. Пусть М и N - алгебраические системы с одинаковым набором опе­раций и без отношений. Тогда декартово произведение М × N будет такой же алгебраи­ческой структурой, если для любой k-арной операции f(a₁,..., a_k), определенной на мно­жествах М и N, на множестве М × N следующим образом определим операцию:

f((m₁, n₁), . . . , (m_k, n_k)) = (f(m₁, . . . ,m_k), f(n₁, . . . , n_k)).

Аналогично опеделяются операции на произведении п алгебраических систем.

Определение 2.11. Пусть М - алгебраическая система, в которой нет отношений. Пред­положим, что на М можно задать отношение эквивалентности ~, согласованное с опе­рациями на М, а именно: для любой n-арной операции f(a₁,... ,а_п), определенной в ал­гебраической системе М и любых элементов из М таких, что m₁ ~ т₁’,..., т_п ~ т_п’ выполняется отношение f(m₁,..., т_п) ~ f(rn₁’,..., т_п’). Тогда множество классов эквива­лентности (М/ ~) превращается в алгебраическую систему с теми же операциями, что действуют на множестве М :

f([m₁]_~ , [m₂]_~, . . . , [m₂]_~) = [f(m₁,m₂, . . . ,m_n)]_~.

Такая алгебраическая система называется фактор-системой алгебраической системы М по отношению эквивалентности ~.

Пример. Всем с детства известна алгебраическая система, где множество М = {чет, нечет}; задана бинарная операция + : чет + чет = нечет + нечет = чет, чет + нечет = нечет + чет = нечет; выделен нулевой элемент: 0 = чет. Такая алгебраическая система фактически яв­ляется фактор-системой алгебраической системы (Z, +, 0) по отношению эквивалентности ~:

z₁ ~ z₂ тогда и только тогда, когда z₁ - z₂ делится нацело на 2.

Определение 2.12. Группой называется множество G с бинарной операцией, обознача­емой обычно ∙, удовлетворяющей трем условиям:

1)операция ∙ - ассоциативна;

2)существует единичный элемент е такой, что g • е = е • g = g для любого g G;

3)все элементы множества G обратимы, то есть для любого g G найдется такой элемент g ^-1 G, что g ∙ g ^-1 = g ^-1 ∙ g = е.

Итак, группа - это моноид, в котором каждый элемент обратим. Заметим, что группа G называется абелевой, если операция ∙ коммутативна.

В группе G можно решить любое уравнение вида а∙х = b или х∙а = b (a,b G). Решением первого уравнения будет х = а ^-1∙b, а второго - х = b ∙ а ^-1. Если операция в группе - сложение, то рассмотренные выше уравнения имеют вид: а + х = b или х + а = b; соответ­ственно решениями будут х = (-а) + b или х=b+(-а), где (-а) - противоположный (обратный) элемент к элементу а.

Примеры.

1. Алгебраические системы (Z, +, 0), (R, +, 0) являются абелевыми группами по сложению.

2. Множество всех невырожденных матриц размера п х п над R относительно обычной операции умножения матриц является группой, которую обозначают GL_n(R).

3. Множество SL_n(R) = {А GL_n(R) | detA = 1} - группа относительно обычной операции умножения матриц, являющаяся подгруппой группы GL_n(R). Такая группа называ­ется специальной линейной группой.

4. Алгебраическая система ({е},-|е∙е = е) является группой, состоящей только из одного единичного элемента. Такая группа называется единичной. Заметим, что в любой группе есть единичная подгруппа.

5. Алгебраическая система ({1,-1} | 1,-1 Z, ∙) - группа из двух элементов относительно обычной операции умножения на Z.

6. Пусть X = {1,2,..., n}. Тогда алгебраическая система (BiX^X,o) является группой всех биективных отображений множества X на себя относительно операции композиции.

Такую группу называют группой подстановок на множестве X. Рассмотрим ее более подробно. Пусть σ ВiХ^X и σ(1) = i₁, σ(2) = i₂,..., σ(п) = i_n. Отображение σ назовем подстановкой и обозначим (i₁, i₂,..., i_n). Подстановка е = (1, 2,..., п), называемая тождественной подстановкой, будет нейтральным элементом, или единицей в группе под­становок на множестве X. Для любого элемента а = (i₁, i₂,..., i_n) из группы подстановок определен обратный элемент σ ^-1 так, что σ⁻¹(i_j) = j, (j {1, 2,…, n}).

Группу подстановок на множестве из п элементов обозначают S_n. Таким образом, BiX^X = S_n. Известен порядок этой конечной группы: |S_n| = |ВiХ^X| = п!. Если п > 3, то группа S_n не является абелевой группой.

Примеры.

1. Пусть на множестве R задано отношение α: хαу тогда и только тогда, когда х² = у². Тогда [1]_α = {1,-1}.

2. В любом множестве X с отношением эквивалентности =: [х]₌ = {х} для любого эле­мента х множества X.

Теорема 1.41. Пусть α отношение эквивалентности на множестве X, X ≠ Ø. Тогда:

1. [х]_а ≠ Ø для любого элемента х множества X;

2. для любых элементов х и у из множества X таких, что [х]_а [у]_а ≠ Ø_; следует, что [х]_а = [у]_а

3)

Доказательство. 1) Отношение α - рефлексивно, следовательно, для любого х из множе­ства X выполняется хαх. Таким образом х [x]_α и [x]_α ≠ Ø.

3) Так как х [х]_α, то , следовательно

2) Пусть [х]_α [у]_α ≠ Ø. Тогда найдется такой элемент z множества X, что xαz и yαz. Пусть t - произвольный элемент из класса [х]_α Тогда xαt и xαz, следовательно, выполняется tαz (мы воспользовались транзитивностью и симметричностю). Аналогично, так как tαz и yαz, то tαy. Таким образом [х]_α [у]_α. Точно также доказывается, что [у]_α [х]_а , и свойство 2) доказано.

Определение 1.42. Пусть α - отношение эквивалентности на множестве X. Фактор-множеством множества X по отношению эквивалентности α называется множество, обозначаемое Х/α, элементами которого являются классы эквивалентности [х]_α множества X по отношению эквивалентности α.

Определение 1.43. Пусть α - отношение эквивалентности на множестве X. Множество X' (X' X) называется системой различных представителей по отношению эквива­лентности α, если для любого х из множества X выполняется условие: |Х' [х]_α | = 1.

Заметим, что можно выбирать различные системы представителей по отношению эквивалентности α на множестве X, однако количество элементов в каждой такой системе одно и тоже. Справедлива следующая теорема, которую мы сформулируем без доказательства.

Теорема 1.44. Если α - отношение эквивалентности на множестве X, X' - система различных представителей по отношению эквивалентности α на множестве X, то существует биективное отображение φ : Х/α → X'. В частности, если Х/α -конечное множество, то |Х/α| = |Х'| .

Отношение эквивалентности на множестве обычно обозначают знаком ~.

Пример. На множестве Z рассмотрим следующее отношение эквивалентности: z₁ ~ z₂ тогда и только тогда, когда z₁ — z₂ делится нацело на 2. Тогда множество Z разбивается на два непересекающихся класса эквивалентности:

[0]_~ = {0,±2,±4,...,±2n,...},

[1]_~ = {±1,±3,...,±(2n+1),...}.

Любая система различных представителей в этом случае содержит 2 элемента. Напри­мер, {0,1} и {4,-5} - системы различных представителей множества Z по отношению эквивалентности ~.

Подграфы

Граф Н называется подграфом графа G, если VH VG, ЕН EG. Подграф Н называется остовным подграфом (или фактором), если VH = VG. Если множество ребер U = ЕН совпадет с множеством всех ребер графа G, оба конца которых принадлежат VH, то Н называется подграфом, порожденным множеством U. На рис.5 изображены граф G и три его подграфа H₁, Н₂ и H₃, среди которых H₃ является остовным, a Н₂ - порожденным.

Важный класс подграфов составляют подграфы, полученные в резуль­тате удаления вершины v VG. Граф G_v = G - v получается из графа G в результате удаления вершины v и всех инцидентных ей ребер. С графами G_v связана знаменитая гипотеза.

Гипотеза реконструируемости (П. Кэлли, С. Улам, 1945 г.). Пусть G и H - два графа одного порядка п > 2 и система {G_v|v VG} совпадает с системой {H_u|u VH} в том смысле, что вершины можно перенумеровать так, что G_vH_u, для всех i. Тогда G Н.

Подтверждена реконструируемость графов для 3 ≤ п ≤ 10. Заметим, что для п = 2 эта гипотеза не верна. Операции над графами

Удаление вершины или ребра - это пример операций, уменьшающих число элементов графа. Рассмотрим теперь операции над графами, уве­личивающими число вершин или ребер. Такова, например, операция добавления ребра е = uv, если вершины u и v графа G не являются смежными. В результате получается граф G + е, у которого эти вер­шины уже соединены ребром.

Граф H называется объединением (или наложением) графов F и G, если VH = VFVG и ЕН = EFEG (рис.6). В этой ситуации пишут H=FG

Объединение FG называется дизъюнктным, если VF VG = Ø.

Пусть G_i m (V_i, E_i) (i = 1, 2)- два графа. Произведением G₁ G₂ = G называется граф, для которого VG = V₁ V₂ - декартово произведе­ние множеств вершин исходных графов, a EG определяется следующим образом: вершины (и₁ , и₂) и (w₁ , w₂) смежны в графе G тогда и только тогда, когда или и₁₌w₁ , а и₂ и w₂ смежны в G₂ , или и₂₌w₂ , а и₁ и w₁ смежны в G₁ (см. рис.7).

Рис. 7

Очевидно, что |G₁ G₂ | = |G₁| |G₂ |, |E(G₁ G₂ )| = |G₁ | |EG₂ | + |G₂ | |EG₁ |

С помощью операции произведения вводится рекуррентным образом важный класс графов – п-мерные кубы Q_n: Q₁=K₂; Q_n=K₂Q_n-1 (n>l).

Граф Q_n имеет порядок 2^п, вершины его можно представить (0,1)-векторами длины п таким образом, что две вершины будут смежны тогда и только тогда , когда соответствующие векторы различаются ровно в одной координате.

Матрицы, ассоциированные с графом

В этом параграфе и далее (i,j)-й элемент матрицы М обозначает­ся M_ij. Пусть G - помеченный граф порядка п, VG = {1,2,... ,п}. Определим п n - матрицу А = A(G), положив

A(G) называется матрицей смежности графа G. Это симметрическая матрица с нулями на главной диагонали.

Теорема. Графы изоморфны тогда и только тогда, когда их ма­трицы смежности получаются друг из друга одинаковыми переста­новками строк и столбцов.

Так как при такой перестановке строк и столбцов не меняется ранг, характеристический многочлен и корни характеристического многочле­на, то имеет смысл для графа G определить ранг - rankG, как ранг матрицы A(G), характеристический полином графа и спектр графа как множество всех корней характеристического полинома (корни ве­щественны в силу симметричности матрицы A(G)).

Если спектры двух графов различны, то они не изоморфны. Обрат­ное, однако, не верно, как показывает пример неизоморфных графов K_1,4 и С₄ O₁, у которых один и тот же характеристический полином х³(x² - 4).

Вторая из матриц В = B(G) графа G называется матрицей Кирхго­фа

Сумма элементов в каждой строке и в каждом столбце матрицы B(G) равна 0. Теорема остается справедливой и для матрицы Кирхгофа.

17. Метрические характеристики графов. Деревья. Планарность графов.

Метрические характеристики графа

В этом параграфе G - связный граф.

1. Пусть и и v - две несовпадающие вершины графа G. Длина кратчайшего (u,v) - маршрута называется расстоянием между вершинами и и v и обозначается через d(u,v). Положим также d(u,u) = 0.

Теорема 1. Расстояние d(u, v) удовлетворяет аксиомам метрики:

а) d(u,v) ≥ 0;

б) d(u, v) = 0 тогда и только тогда, когда и = v; в)d(u,v) = d(v,u);

г) d(u,v) + d(v,w) ≥ d(u, w)

для любых вершин и, и, w графа G.

Понятие расстояния между вершинами позволяет определить k-ю степень графа G. Граф G^k имеет то же множество вершин, что и G и несовпадающие вершины u и v смежны в графе G^k в том и толь­ко том случае, если d(u,v) ≤ k. Диаметром d(G) графа G называется наибольшее из расстояний. Ясно, что d(G) ≤ |G|.

Теорема 2. Если k ≥ d(G), то G^k - полный граф.

Теорема 3. Для любого связного графа G имеет место неравен­ство: d(G) ≤ rankG.

2. Критерий двудольности графа.

Теорема 3 (Кениг, 1936 г.). Для двудольности графа необходимо и достаточно, чтобы он не содержал циклов нечетной длины.

Деревья

Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим или лесом. Следующая тео­рема характеризует и дает эквивалентные определения дереву.

Теорема 1. Для (п, т)-графа G следующие условия эквивалентны:

а) G - дерево;

б) G - связный граф и т = п - 1;

в) G - ациклический граф и т = п - 1;

г) любые две несовпадающие вершины графа G соединяет единственная простая цепь.

Следствие. В любом дереве порядка п ≥ 2 имеется не менее двух концевых вершин.

Пусть Н - остовной подграф произвольного графа G. Если на каждой области связности графа G графом H порождается дерево, то Н назы­вается остовом или каркасом графа G. Очевидно, что в любом графе существует остов: разрушая в каждой компоненте циклы, т.е. удаляя лишние ребра, придем к остову.

Теорема 2. Число ребер произвольного графа G, которые необхо­димо удалить для получения остова, не зависит от последовательно­сти их удаления и равно m(G) - |G| + k(G), где m(G) и k(G) - число ребер и число компонент графа G соответственно.

Планарность

Встречаются ситуации (например в радиоэлектронике при проекти­ровании путей коммуникаций), когда важно выяснить, возможно ли на­рисовать граф на плоскости так, чтобы его изображение удовлетворяло определенным требованиям. Таким образом возникает понятие плоско­го графа. Плоским графом назовем граф, вершины которого являют­ся точками плоскости, а ребра - непрерывными плоскими линиями без самопересечений, соединяющими соответствующие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины. Любой граф, изоморфный плоскому графу, будем называть планарным. О планарных графах говорят, что они укладываются на плоскости. Имеет смысл рассматривать укладки и на других поверх­ностях (например, сфере, торе, сфере с п ручками), а также в простран­стве.

Теорема 1. Для любого графа найдется натуральное число п та­кое, что данный граф укладывается на сфере с п ручками. Тем более любой граф укладывается в пространстве.

Наименьшее натуральное число п со свойством, указанным в теореме 1, называется родом графа G и обозначается γ(G). В случае γ(G) = 1 говорят о тороидальных графах. Что касается взаимоотношений планарности и возможности укладки на сфере, то ответ дается в следующей теореме.

Теорема 2. Граф укладывается на сфере тогда и только то­гда, когда он планарен, что в свою очередь эквивалентно равенству γ(G) = 0.

Доказательство легко получается с помощью стереографической проекции. Южный полюс сферы помещаем на плоскость и проектиру ем из северного полюса. При этом, если граф уложен на сфере, счи­таем, что северный полюс не принадлежит ни одному ребру графа, а если граф уложен на плоскости, то южный полюс обладает таким же свойством (очевидно, что даже малым сдвигом графа можно обеспечить соблюдение этого условия)

Существуют ли непланарные графы? Да, существуют, граф K_3,3 не является планарным, как мы увидим позже. Более того, почти все графы непланарны в том смысле, что предел отношения

количество непланарных графов порядка n

количество всех графов порядка п

равен единице при п →.

Гранью плоского графа называется максимальное по включению мно­жество точек плоскости, каждая пара которых может быть соединена непрерывной кривой, не пересекающей ребра графа. Границей грани будем считать множество вершин и ребер, принадлежащих этой гра­ни. Далее будем пользоваться следующими обозначениями: n, m, f -соответственно число вершин, ребер и граней плоского графа.

Теорема 3 (Эйлер, 1758 г.). Для всякого связного плоского графа верно равенство (формула Эйлера) п - т + f = 2.

Именно с помощью формулы Эйлера доказывается непланарность не­которых графов.

Предложение. Графы К₅ и К_3,3 непланарны.

Особая роль непланарных графов К₅, К_3,3 заключается в том, что эти графы являются минимальными непланарными графами и играют важную роль во многих критериях планарности. Имеется несколько критериев планарности графа. Мы рассмотрим только один.

Теорема 4 (Понтрягина - Куратовского). Граф планарен тогда и только тогда, когда он не содержит подграфов, гомоморфных К₅ или К_3,3.

18. Высказывание. Операции над высказываниями. Булева алгебра высказываний.

Алгебра высказываний.

Основным понятием в этом параграфе является высказывание. В определении, которое следует далее, мы используем интуитивные представления о том, что есть истина и что - ложь.

Определение 3.1. Высказывание - это повествовательное предложение, о котором мож­но сказать, истинно оно или ложно.

Рассмотрим следующие предложения.

1. 2 + 2 = 4.

2. Для любого х из R выполняется неравенство х² + 1 < 0.

3. Город Москва является столицей России.

4. Если x R, то x² - 1 < 0.

5. Длина отрезка меньше площади треугольника.

Предложения 1) и 3) - истинные высказывания; 2) - ложное высказывание; предложения 4) и 5) не являются высказываниями.

Пусть А - множество всех высказываний, Е₂ = {0,1}. Определим отображение â : А —> Е₂ следующим образом: â = 0, если a - ложное высказывание; â = 1, если а - истинное высказывание. При этом â назовем значением истинности высказывания а.

Определение 3.2. Выск-ия а и b будем называть равносильными и писать а ≡ b, если â = .

Заметим, что это определение - естественно, так как при рассмотрении высказываний нас не интересует содержательная часть, заключенная в предложении, а интересует только значение его истинности.

На множестве всех высказываний с помощью значений истинности определим следующие операции, которые называют логическими.

Определение 3.3. Отрицанием высказывания а называется высказывание, обозначае­мое , определяемое следующей таблицей:

Очевидно, что = а. Сформулированное равенство называют законом двойного отрица­ния.

Заметим, что отрицание - это унарная операция, определенная на множестве высказыва­ний А и соответствующая конструкции = {Не ... }, если а = {…} - высказывание. Далее на множестве высказываний А определим бинарные операции.

Определение 3.4. Конъюнкцией высказываний аиb называется высказывание, обозна­чаемое а b или а ∙ b и определяемое таблицей:

Очевидны следующие свойства конъюнкции:

1. аb≡ bа- коммутативность;

2. а (b с) = (а b) с - ассоциативность;

3. a 1 ≡а;

4. a 0 ≡ 0;

5. a a ≡ а.

Заметим, что здесь, и в дальнейшем символом 0 мы обозначаем ложное высказывание, а символом 1 - истинное. Конъюнкция, логическое умножение, соответствует союзу "и" в

русском языке. Например, если высказывание а ≡ (− − −), b ≡ (***), то высказывание

а b = ((− − −) и (* * *)).

Определение 3.5. Дизъюнкцией высказываний а и b называется высказывание, обозна­чаемое а b и определяемое следующей таблицей истинности:

Очевидны следующие свойства дизъюнкции:

1) а b = b а - коммутативность;

2) а (b с) ≡ (а b) с - ассоциативность;

3) a1 ≡ 1; 4) a 0 ≡ а; 5) a a ≡ а.

Дизъюнкция, логическое сложение, соответствует союзу "или" в русском языке. Если вы­сказывание а = (-----), высказывание b = (***), то высказывание аb = ((-----)или(***)).

Определенные нами на множестве высказываний А операции: отрицание, конъюнкция, дизъюнкция, - называются булевыми операциями. Алгебраическая структура (А, , , ) называется булевой алгеброй, так как в ней выполняются следующие 19 равносильностей для булевых операций.

21. Двойственность в алгебре высказываний. Теорема о общем принципе двойственности для булевых формул.

Определение 3.17. Пусть f(x₁, x₂,..., х_п) - формула алгебры высказываний. Двойствен­ной к ней будем называть формулу f*(x₁, x₂,... ,х_п) = .

Утверждение. Справедливы следующие равносильности:

1. (f*)* ≡f, 2) (0)* ≡ 1, 3) (1)* ≡0, 4) (х)* ≡ х, 5) (х)* ≡ х, 6) (х у)* ≡ х V у, 7) (x у)* ≡ x у.

Доказательство каждого из пунктов следуют непосредственно из определения. Напри­мер,

1) (0*) ≡ ≡ 1; 7) (x у)* = = = x y.

Теорема 3.18. f₁(x₁, x₂,... ,х_п) ≡ f₂(x₁, x₂,... ,х_п) - равносильные формулы в алгебре высказываний тогда и только тогда, когда f₁^*(x₁, x₂,...,х_п) ≡ f₂^*(x₁, x₂,... х_п) - равно­сильные формулы в алгебре высказываний.

Доказательство. Заметим, что столбец ^* в таблице истинности формулы f* может быть получен из столбца в таблице истинности формулы f с помощью инвертирования, то есть симметрии относительно середины таблицы по строкам и отрицания:

Отсюда сразу следует, что, если совпадают таблицы истинности формул f₁ и f₂, то совпа­дают и таблицы истинности формул f₁^* и f₂^* . Теорема доказана.

Теорема 3.19. Общий принцип двойственности. Пусть G(x₁, x₂,... ,x_n) = F(f₁(x₁, x₂,... ,x_n),f₂(x₁, x₂,... ,x_n),... ,f_m(x₁, x₂,... ,x_n)) .