Пример выполнения работы № 5
1. Вычислить повторные интегралы:
а)
;
б)
.
2. Вычислить кратные интегралы:
а)
,
где область
ограничена линиями
;
б)
,
где область
ограничена поверхностями
.
1. а) Введем повторный интеграл из условия задачи и вычислим его
>Int(Int(3*x*y^2+1,y=0..sqrt(x)),x=0..2)= int(int(3*x*y^2+1,y=0..sqrt(x)), x=0..2);
б) Введем повторный интеграл и вычислим его
>Int(Int(Int(4*z^2*x-3*y,z=0..x^2+2*y^2),y=-x..x^2),x=0..1)= int(int(int(4*z^2*x-3*y,z=0..x^2+2*y^2),y=-x..x^2),x=0..1);
2. а) Область
интегрирования представляет собой
множество
.
Построим
область
.
> m:=plot([-sqrt(x),x^2],x=1..2,color=[red,red]):
>with(plots):
> k:=implicitplot(x=1,x=1..2,y=-1..1,color=red):
>k1:=implicitplot(x=2,x=1..2,y=-sqrt(2)..4,color=red):
> display([m,k,k1]);
Вычислим двойной
интеграл как повторный
.
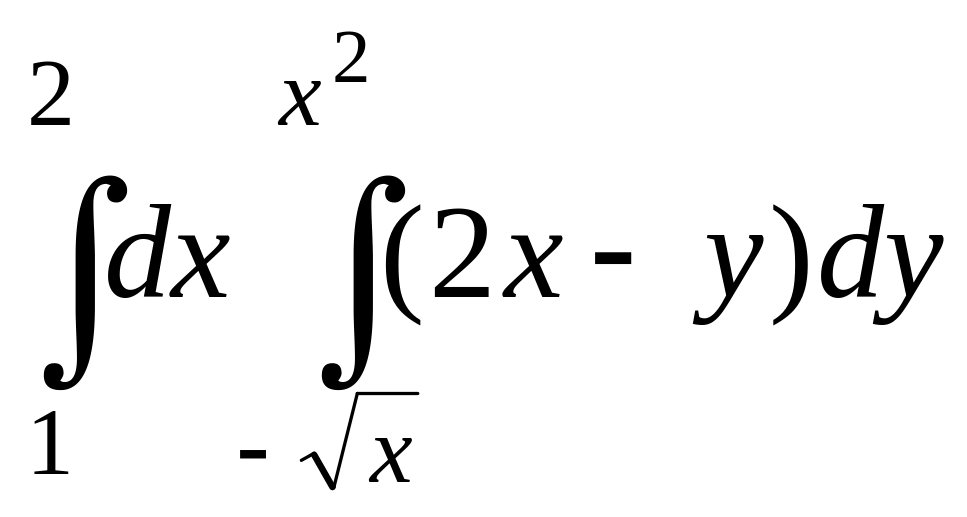>Int(Int(2*x-y,y=-sqrt(x)..x^2),x=1..2)= int(int(2*x-y,y=-sqrt(x)..x^2),x=1..2);
=
б) Область интегрирования можно задать системой неравенств:
.
Построим проекцию области
на
плоскость
.
> m:=plot([x+1,x^2],x=0..1,color=[red,red]):
> k:=implicitplot(x=0,x=0..1,y=0..1,color=red):
>k1:=implicitplot(x=1,x=0..1,y=1..2,color=red):
> display([m,k,k1]);
Тогда тройной
интеграл сводится к повторному
.
> Int(Int(Int(3*z-1,z=0..x+y),y=x^2..x+1),x=0..1)= int(int(int(3*z-1,z=0..x+y),y=x^2..x+1),x=0..1);
=
Контрольные вопросы
1. Сформулируйте определение двойного интеграла.
2. В чем состоит геометрический смысл двойного интеграла?
3. Какими свойствами обладает двойной интеграл?
4. Сформулируйте теорему о сведении двойного интеграла к повторному.
5. Что представляет собой определитель Якоби? Как производится замена переменных в двойном интеграле?
6. Как производится вычисление двойного интеграла в полярных координатах?
7. Сформулируйте определение тройного интеграла.
8. В чем состоит геометрический смысл тройного интеграла?
9. Сформулируйте теорему о сведении тройного интеграла к повторному.
10. Как производится вычисление тройного интеграла в цилиндрических и сферических координатах?
ПРИЛОЖЕНИЕ
Запись некоторых (элементарных) функций в Maple
Математическая запись |
Maple-запись |
Математическая запись |
Maple-запись |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Говорухин В. Компьютер в математическом исследовании Maple, MATLAB, LaTeX. Учебный курс [Текст] / В. Говорухин, В. Цибулин. – СПб. : Питер, 2001. – 624 с.
2. Дьяконов В. Maple 7: учебный курс. [Текст] / В. Дьяконов. – СПб. : Питер, 2002. – 672 с.
3. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты: Учебное пособие. 4-е изд., стер. [Текст] / Л.А. Кузнецов – СПб. : Издательство «Лань», 2005. – 240 с.
4. Высшая математика для экономистов [Текст]: учебник для вузов/ Н.Ш. Кремер [и др.]; под редакцией Н.Ш. Кремера.- 3-е изд. – М.: ЮНИТИ, 2007. – 479 с.
5. Ефимов А. В. Сборник задач по математике для втузов [Текст] : [учеб. пособие для втузов]: в 4 ч. Ч. 2 / А. В. Ефимов [и др.] ; под общ. ред. А. В. Ефимова, А. С. Поспелова. - 4-е изд., перераб. и доп. - М. : Физматлит, 2004. - 432 с.
6. Натансон, И.П. Краткий курс высшей математики [Текст]: учеб. Пособие для вузов / И.П. Натансон. – 9-е изд., стер. – СПб.: Лань, 2007. – 736 с.
7. Шипачев, В.С. Высшая математика [Текст] / В. С. Шипачев. - М.: Высш. шк., 2008.
8. Шипачев, В.С. Математический анализ [Текст] : учеб. пособие для вузов / В. С. Шипачев. - М.: Высш. шк., 2002. - 176 с.