2 Ортогональне центральне композиційне планування

2.1 Перетворення керованих факторів

При плануванні експерименту проводять перетворення розмірних керованих незалежних чинників в безрозмірні, нормовані:

це дає можливість легко побудувати ортогональну МП і значно полегшує подальші розрахунки, оскільки в цьому випадку верхні і нижні рівні варіювання і у відносних одиницях рівні відповідно +1 і -1 незалежно від фізичної природи чинників, значень основних рівнів і інтервалів варіювання факторів .

Якщо для трьох факторів задати теоретичне рівняння регресії відносно нормованих факторів має вигляд

,

тобто ступенями факторів вище за першу можна знехтувати, то ПФЕ дає можливість знайти роздільні оцінки коефіцієнтів . Оскільки зміна вихідної величини носить випадковий характер, то є можливість визначити лише вибіркові коефіцієнти регресії і для оцінювання теоретичних коефіцієнтів , .

У разі ОЦКП критерієм оптимальності плану є ортогональность стовпців МП. Через ортогональністі планування всі оцінки коефіцієнтів визначаються незалежно один від одного.

2.2 Планування. Вказаний вище критерій оптимальності плану приводить до побудови МП з ортогональними вектор стовпцями, у тому числі і для і . Ортогоналізацію стовпців і проводять за допомогою перетворення

де N — загальне число рядків МП. неважко помітити, що в цьому випадку умова ортогональності виконується, тобто

Окрім стовпців і ортогоналізації підлягають вектор-стовпці і . З умови ортогональності перетворених вектор-стовпців і , має вигляд

виводиться рівняння для розрахунку величини зіркового плеча:

де — величина зоряного плеча; — число крапок ПФЕ (ДФЕ); — число центральних точок; — число «зіркових точок» крапок для квадратів

В табл. 7.2 приведені параметри ОЦКП для числа чинників n = 2; 3; 4

Таблиця 2.

n
2	1,0	4	1	4	9
3	1,215	6	1	8	15
4	1,414	8	1	16	25

Групы точек	g
	1 2 3 4 5 6 7 8	+1 +1 +1 +1 +1 +1 +1 +1	-1 +1 -1 +1 -1 +1 -1 +1	-1 -1 +1 +1 -1 -1 +1 +1	-1 -1 -1 -1 +1 +1 +1 +1	0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27	0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27	0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27	+1 -1 -1 +1 +1 -1 -1 +1	+1 -1 +1 -1 -1 +1 -1 +1	+1 +1 -1 -1 -1 -1 +1 +1
	9 10 11 12 13 14	+1 +1 +1 +1 +1 +1	-1,215 +1,215 0 0 0 0	0 0 -1,215 +1,215 0 0	0 0 0 0 -1,215 +1,215	+0,75 +0,75 -0,73 -0,73 -0,73 -0,73	-0,73 -0,73 +0,75 +0,75 -0,73 -0,73	-0,73 -0,73 -0,73 -0,73 +0,75 +0,75	0 0 0 0 0 0	0 0 0 0 0 0	0 0 0 0 0 0
	15	+1	0	0	0	-0,73	-0,73	-0,73	0	0	0

Матриця ОЦКП для трьох незалежних змінних приведена в табл.3, де . Таблиця 7.3

2.3 Проведення експерименту. Точно так, як і при проведенні ПФЕ, через випадковий характер зміни вихідної величини в кожній g—ой точці (де g=1,2., N), доводиться проробляти m паралельних дослідів і результати спостереженнь усереднювати:

Варіанти варіювання в кожній серії випробувань або всі досліди всіх m серій рандомізують.

2.4 Перевірка відтворності експерименту є не що інше, як перевірка виконання другої передумови регресійного аналізу про однорідність вибіркових дисперсій . Задача полягає в перевірці гіпотези про рівність генеральних дисперсій при дослідах відповідно в крапках . Оцінки дисперсій знаходять по відомій формулі

Оскільки всі оцінки дисперсій одержані по вибірках однакового об'єму m=3, то число ступенів свободи для всіх них однакове і складає

.

В цьому випадку для перевірки гіпотези про однорідність оцінок дисперсій слід користуватися критерієм Кохрена, який заснований на законі розподілу відношення максимальної оцінки дисперсії до суми всіх порівнюваних оцінок дисперсій, тобто

.

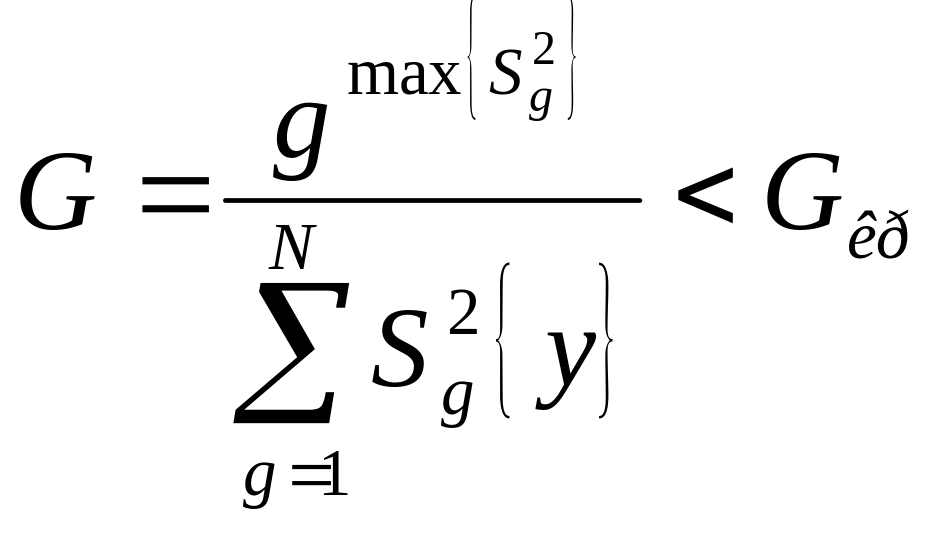Якщо обчислене за даними експерименту (емпіричне) значення критерію G виявиться менше критичного значення , знайденого по таблиці (див. Додаток X або ХІ) для і в даному випадку і ) і вибраного рівня значущості (звичайно 5%), то гіпотеза про однорідність вибіркових дисперсій відповідає результат спостережень. При цьому всю групу вибіркових дисперсій можна вважати оцінками для однієї і тієї ж генеральної дисперсії відтворності експерименту, звідки якнайкраща її оцінка має вигляд

з числом ступенів свободи

Якщо перевірка відтворності експерименту дала негативний результат, то залишається визнати його не відтворюваність відносно керованих факторів унаслідок наявності несприятливих флуктуації некерованих і неконтрольованих чинників. При цьому необхідно або збільшити число паралельних дослідів для варіантів варіювання з великими значеннями вибіркових дисперсій , або використовувати надалі модифікацію методу найменших квадратів, придатну при невиконанні передумови про відтворність експерименту.

2.5 Отримання математичної моделі об'єкту. Оцінки коефіцієнтів рівняння регресії визначають по формулі

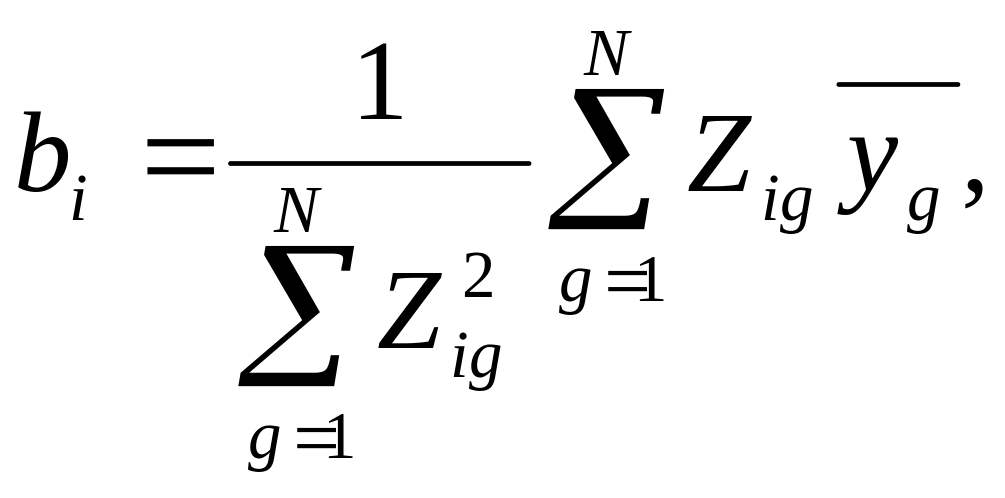
а дисперсії оцінок коефіцієнтів — по формулі

.

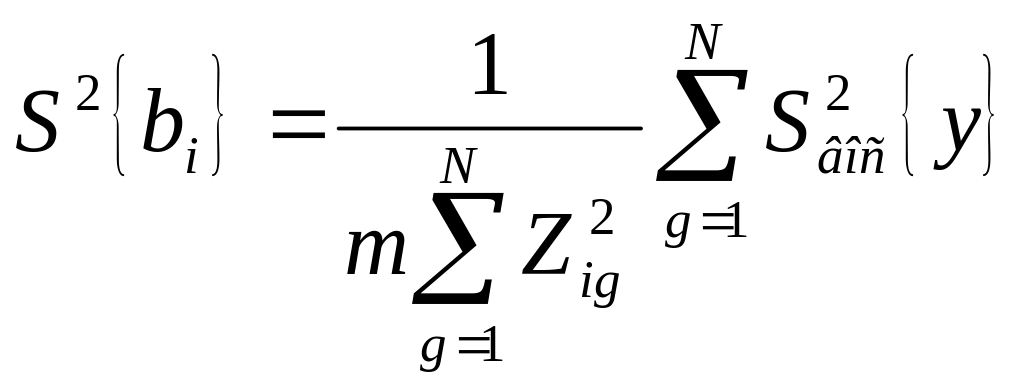Оскільки знаменник у формулах (14) і (15) в загальному випадку різний для різних груп оцінок коефіцієнтів , то оцінки дисперсії (15) однакові тільки всередині даної групи оцінок коефіцієнтів.