
Точкова оцінка математичного сподівання
Нехай х1, х2,..., хn - вибірка, отримана в результаті n незалежних випробувань над випадковою величиною Х - деякою ознакою генеральної сукупності, яка має математичне сподівання M(Х) = а.
За точкову оцінку математичного сподівання а = M(Х) беруть вибіркове середнє:
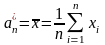
Припустимо
додатково, що випадкова величина Х
має
скінченну
дисперсію
D(Х)
=
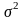 .
Тоді
можна стверджувати, що оцінка
.
Тоді
можна стверджувати, що оцінка
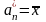 є
слушною.
є
слушною.
Приймемо
без доведення важливе для практики
твердження:
якщо
випадкова величина Х нормально
розподілена з параметрами M(Х)=
а і
D(Х)
=
,
то
оцінка
має у класі всіх незміщених оцінок
математичного
сподівання
а
мінімальну дисперсію, яка дорівнює
 .
Тому
.
Тому
![]() є ефективною
оцінкою
параметра а.
є ефективною
оцінкою
параметра а.
Точкова оцінка дисперсії. Підправлена дисперсія
Якщо
випадкова вибірка складається з
результатів n
незалежних випробувань х1,
х2,...,
хn
над випадковою величиною Х із математичним
сподіванням M(Х)
= а
і дисперсією D(Х)
=
,
то за точкову оцінку дисперсії беруть
вибіркову дисперсію
 ,
яка
є зміщеною
оцінкою параметра D(Х)
=
,
або підправлену вибіркову дисперсію
,
яка
є зміщеною
оцінкою параметра D(Х)
=
,
або підправлену вибіркову дисперсію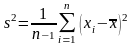 .
.
Враховуючи
співвідношення
 одержимо
одержимо
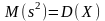 ,
тобто дисперсія
,
тобто дисперсія
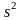 є
незміщеною оцінкою для дисперсії
D(Х)
=
.
є
незміщеною оцінкою для дисперсії
D(Х)
=
.
Дріб
 називають поправкою Бесселя. Для малих
значень n
поправка
Бесселя значно відрізняється від
одиниці. Для n>50
практично немає різниці між DB
i
s2.
Оцінки DB
i
s2.є
слушними і не є ефективними.
називають поправкою Бесселя. Для малих
значень n
поправка
Бесселя значно відрізняється від
одиниці. Для n>50
практично немає різниці між DB
i
s2.
Оцінки DB
i
s2.є
слушними і не є ефективними.
У
випадку, коли математичне сподівання
а
відоме і випадкова величина Х нормально
розподілена, то незміщеною, слушною та
ефективною оцінкою дисперсії D(Х)
=
є оцінка
 .
.
Теоретичний параметр |
Статистична оцінка |
|
для не згрупованих даних |
для згрупованих даних |
|
Математичне сподівання
|
Вибіркове середнє
|
Вибіркове середнє
|
Дисперсія
|
Зміщена оцінка
(виправлена дисперсія)
|
Зміщена оцінка
Незміщена оцінка (виправлена дисперсія)
|
Початковий s-ий момент
|
Вибірковий початковий s-ий момент
|
Вибірковий початковий s-ий момент
|
Центральний s-ий момент
|
Центральний вибірковий s-ий момент
|
Центральний вибірковий s-ий момент
|
Коефіцієнт
асиметрії
|
Вибірковий
коефіцієнт асиметрії
|
|
Ексцес
|
Вибірковий
ексцес |
|
Коефіцієнт
варіації
|
Вибірковий
коефіцієнт варіації
|
|
Приклад 5. У результаті статистичних досліджень випадкової величини Х отримано таку вибірку: 47, 45, 46, 45, 46, 47, 44, 46, 45, 46, 45, 46, 46, 44, 46, 48, 46, 45, 46, 47, 44, 46, 45, 45, 46, 44, 46, 48, 46, 46, 45, 47, 44, 46, 45, 45, 44, 48, 46, 46, 45, 47, 44, 46, 45, 46, 46, 47, 46, 47. Знайти незміщені оцінки генерального середнього та генеральної дисперсії.
xi |
44 |
45 |
46 |
47 |
48 |
ni |
6 |
11 |
23 |
7 |
3 |
Розв’язання. Обсяг вибірки n=50. Побудуємо статистичний розподіл вибірки:
Перейдемо
до умовних варіант для полегшення
розрахунків
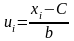 ,
де С=46,
b=1.
,
де С=46,
b=1.
Незміщеною оцінкою генерального середнього є вибіркове середнє:
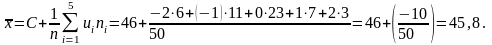
Щоб знайти незміщену оцінку генеральної дисперсії – виправлену вибіркову дисперсію, визначимо вибіркову дисперсію й помножимо на коефіцієнт Бесселя:

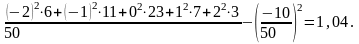
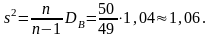
╚═


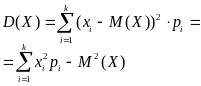
 Незміщена
оцінка
Незміщена
оцінка