Самостійна робота № 12

Тема: Розв’язування задач з теми «Числові характеристики статистичного розподілу вибірки».

Мета: Закріпити набуті знання та навички, перевірити їх при виконанні практичних завдань.

Завдання

1. Засвоїти теоретичний матеріал згідно теми;

2. Дати відповіді на поставлені питання (лекція 12);

3. Виконати письмово приведені завдання;

4. Випишіть питання, що виникли в ході засвоєння матеріалу;

5. Зробіть висновки.

Рекомендована література:

1. Барковський В.В. Теорія ймовірностей та математична статистика – К: Центр учбової літератури, 2010р.

2. Кочетков Е.С. Теорія ймовірностей і математична статистика – М: Форум, 2011р

Числові характеристики статистичного розподілу вибірки

У практичних задачах часто замість повного вивчення даних вибірки буває достатньо обмежитися знаходженням їхніх числових характеристик. Далі наведемо основні з них, припускаючи, що статистичні дані згруповано в дискретний варіаційний ряд.

Вибірковим середнім статистичного розподілу вибірки називається середнє арифметичне значення її варіант х_і з урахуванням їхніх частот, тобто .

Вибіркове середнє х є основною характеристикою статистичного розподілу вибірки. Його узагальненням є поняття початкового емпіричного моменту.

Початковим емпіричним моментом S-го порядку M_S статистичного розподілу вибірки називається середнє арифметичне значення степенів порядку S варіант х_i, тобто:

Якщо S = 1, то М₁ = - дорівнює вибірковому середньому.

Переходимо до означення основних характеристик розсіювання значень випадкової величини навколо її середнього значення, які також розраховуються на основі вибірки.

Розмахом вибірки Х називають різницю між найбільшим і найменшим значеннями її варіант, тобто: R = x_k - x₁.

Вибірковою дисперсією D_B статистичного розподілу вибірки називають середнє арифметичне значення квадратів відхилень варіант х_i від вибіркового середнього х, тобто: θ^*_n = θ^*_n( х₁, х₂,..., х_n)

Для обчислення вибіркової дисперсії часто зручніше використовувати іншу формулу:

Розмірність дисперсії дорівнює квадрату розмірності значень випадкової величини, що створює незручність у дослідженнях. Щоб її усунути, за характеристику розсіювання значень випадкової величини за результатами вибірки приймають вибіркове середнє квадратичне відхилення , яке визначається рівністю:

Коефіцієнтом варіації V статистичного розподілу вибірки називається відношення вибіркового середнього квадратичного відхилення до вибіркового середнього, тобто:

Центральним емпіричним моментом S-го порядку m_S статистичного розподілу вибірки називається середнє арифметичне значення степенів порядку S відхилень варіант x_i від середнього вибіркового значення , тобто:

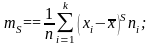
Зокрема, m₁ = 0, m₂ = D_В.

Для оцінки відхилення статистичного розподілу вибірки від нормального розподілу використовують числові характеристики - асиметрію та ексцес.

Асиметрією (коефіцієнтом асиметрії) А_B називають число, яке обчислюється за формулою: , де m₃ - центральний емпіричний момент 3-го порядку, — середнє квадратичне відхилення статистичного розподілу вибірки.

Ексцесом Е_B статистичного розподілу вибірки називається число, яке обчислюється за формулою: 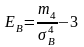, де m₄ - центральний емпіричний момент 4-го порядку, — середнє квадратичне відхилення статистичного розподілу вибірки.

Якщо випадкова величина Х розподілена за нормальним законом, то її асиметрія та ексцес дорівнюють нулю. Тому, що більше віддалені від нуля асиметрія та ексцес, то менше підстав сподіватися, що вибірка, з якої утворено варіаційний ряд, одержана з нормально розподіленої генеральної сукупності.

Приведені співвідношення можуть бути також використані при обчисленні відповідних числових характеристик вибірки для випадків, коли емпіричні дані записані як вихідний статистичний ряд або згруповані за допомогою інтервального варіаційного ряду. Зокрема, у першому з них у згаданих співвідношеннях слід покласти k = n та n_і = 1. У другому випадку ці формули залишаються без змін, якщо вважати, що в них х_і - середини частинних проміжків [z_і-1,z_і), і = 1,2,...,m.

xi	1	3	4	7	10	12	15
ni	5	2	12	7	4	3	2

Приклад 1. Задано статистичний ряд розподілу. Знайти вибіркове середнє, вибіркову дисперсію, середнє квадратичне відхилення вибірки.

Розв’язання. Обсяг вибірки n=5+2+12+7+4+3+2=35.

Вибіркове середнє статистичного розподілу вибірки

╚═

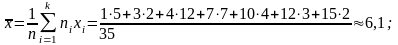
(zi;zі-1]	(0;2]	(2;4]	(4;6]	(6;8]	(8;10]	(10;12]	(12;14]
wi	0,1	0,2	0,3	0,1	0,1	0,1	0,1

Приклад 2. Задано інтервальний статистичний ряд розподілу. Знайти вибіркове середнє, вибіркову дисперсію, середнє квадратичне відхилення вибірки.

Розв’язання. Перетворимо інтервальний статистичний ряд розподілу на точковий: . Отримаємо статистичний ряд:

xi	1	3	5	7	9	11	13
wi	0,1	0,2	0,3	0,1	0,1	0,1	0,1

Вибіркове середнє статистичного розподілу вибірки

╚═

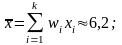
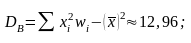
Медіаною Ме називається значення середнього елементу варіаційного ряду. Якщо обсяг вибірки: непарний n=2m+1, Me =x_m+1; парний n=2m,

Приклад 3. На одному з відрізків залізниці планується створити зупинку пасажирського потяга. Розподіл населених пунктів з чисельністю їх населення наведено в таблиці:

На якому кілометрі розташований населений пункт xi	10	12	15	25	28	30	33
Чисельність населення тис.чол. ni	5	2	3	10	1	4	6

На якому кілометрі залізниці потрібно розташувати цю зупинку, щоб сумарна відстань, яку покриватимуть потенційні пасажири до цієї зупинки, була найменшою.

Розв’язання. Оскільки медіана має властивість, що сума абсолютних величин відхилень елементів вибірки від медіани менша, ніж від будь-якої іншої величини, то потрібно знайти медіану.

Обсяг вибірки n=5+2+3+10+1+4+6=31. Отже n=2m+1, Me =x_m+1=х₁₆

В аріаційний ряд: 10,…..,10,12,12,15,15,15,25,….,25,28,30,….,30,33,….,33;