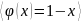Тема 2. Понятие резольвенты интегрального уравнения.
Пусть имеем интегральное уравнение Вольтерра 2 рода
где
есть
непрерывная функция при
а
непрерывна при
.
Будем искать решение интегрального уравнения (3.1) в виде бесконечного степенного ряда по степеням :
(3.2)
Подставляя формально этот ряд в (1), получим
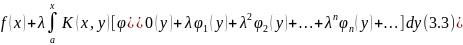
Сравнивая коэффициенты при одинаковых степенях, найдем:
……………………………………………………………………..
Соотношения
(3.4) дают способ последовательного
определения функций
.
Можно показать, что при сделанных
предположениях относительно
полученный таким образом ряд (3.2) сходится
равномерно по
при любом
и
и его сумма есть единственное решение
уравнения (3.1).
Далее, при перестановке двойных интегралов необходимо применить формулу Дирихле; в результате этого получим
Поэтому
за интегрированное ядро
надо взять функцию
Аналогично
устанавливается для любого
Функции
называются повторными или
итерированными ядрами. Они, как
нетрудно видеть, определяются при помощи
рекуррентной формулы
Используя (3.7) и (3.8), равенство (3.2) можно записать так:
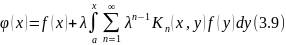
Опр.
Функция
определяемая при помощи ряда
называется резольвентой (или разрешающим ядром ) интегрального уравнения (3.1). Ряд (3.10) в случае непрерывного ядра сходится абсолютно и равномерно.
Приведем две полезные формулы, выражающие решение одного интегрального уравнение через решения других интегральных уравнений.
1.
Пусть решению уравнения Вольтерра
второго рода с ядром
отвечает резольвента
.
Тогда решению уравнения Вольтерра
второго рода с ядро
отвечает резольвента
.
2. Пусть имеются два уравнения Вольтерра второго рода с ядрами
которым соответствуют
резольвенты
.
Тогда уравнение Вольтерра с ядром
имеет резольвенту
Отметим, что в формулах (3.11) и (3.12) интегрирование ведется по различным парам переменных.
Пример
5. Найти резольвенту интегрального
уравнения Вольтерра с ядром
Решение.
Имеем
Далее, формулам (3.7)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
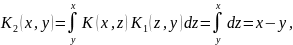
Таким образом, согласно определению резольвента
-------------------------------------------------------------------------------------------------
Тема 3 Связь между линейными дифференциальными уравнениями и интегральными уравнениями Вольтера.
.Сведение дифференциальных уравнений к интегральным.
В ряде случаев решение того или иного дифференциального уравнения целесообразно сводить к решению интегрального уравнения.
Например, для доказательства существования и единственности решения дифференциального уравнения
с
начальным условием
удобно свести его к интегральному
уравнению (нелинейному)
Сведение к интегральному уравнению возможно и для дифференциальных уравнений выше первого порядка.
Рассмотрим, например, уравнение второго порядка
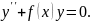
Положив
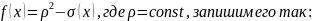
Как известно, решение уравнения
Можно представить в виде
Поэтому, нахождение решения уравнения (1.9) сводится к решению интегрального уравнения
-------------------------------------------------------------------------------------------------
.Сведение дифференциальных уравнений к интегральным.
В ряде случаев решение того или иного дифференциального уравнения целесообразно сводить к решению интегрального уравнения. Например, для доказательства существования и единственности решения дифференциального уравнения
с начальным условием удобно свести его к интегральному уравнению (нелинейному)
Сведение к интегральному уравнению возможно и для дифференциальных уравнений выше первого порядка.
Рассмотрим, например, уравнение второго порядка
Положив
Как известно, решение уравнения
Можно представить в виде
Поэтому, нахождение решения уравнения (1.9) сводится к решению интегрального уравнения
Рассмотрим пример решения уравнения Вольтерра методом дифференцирования.
y(x)
+
=
Решение
Дифференцируя дважды по x, получаем:
(x)
+ 2y(x)+
= 2x
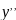(x)
+ 2
(x)
+ y(x) = 2 ……(1)
При x=0: y(0) =0 и (0)=0…….(2)
Характеристическое
уравнение для дифференциального
уравнения 2-го порядка имеет вид:
+
2k + 1 = 0
Его
корни
=
=
- 1
Общее решение для соответствующего однородного уравнения имеет вид:
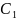Y(x)
=
(
+
x)
Найдем частное решение неоднородного уравнения по виду правой части:
Ф (х) = А, где А=2
Общее решение неоднородного уравнения:
y(x) = Y(x) + ф(x)
y(x) = ( + x) +2 …..(3)
Найдем
производную
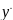(x)
= -
(
+
x)
+
Из условий (2) найдем при x=0:
y(0)
=
(
+
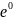0)
+2 = 0,
=
-2
(0)
= -
+
=
0,
=
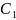-2
Окончательно, y(x) = -2 ( 1+x) +2
2/.Решить уравнение
Продифференцируем уравнение дважды:
Решая получившиеся дифференциальное уравнение, с учетом условий
находим
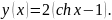
Задание для самостоятельной работы:
Методом дифференцирования решить следующие интегральные уравнения
