Тема 1. Существование и единственность решения интегрального уравнения Фредгольма (метод малого параметра)

Рассмотрим уравнение

(1)

где y(x), f(x) непрерывны на [a, b], а - непрерывна в основном квадрате:

a≤x, ξ≤b.

Будем искать решение в виде ряда

, (9)

где функции подлежат определению.

Предположим, что ряд (9) равномерно сходится и y(x) – решение уравнения (1), тогда (9)→(1):

Приравняем коэффициенты в степенных рядах при одинаковых степенях λ, тогда

(10)

Таким образом, формальное решение уравнения (1) определяется формулами (9)-(10).

Покажем, что ряд (9) действительно равномерно сходится (этим самым результат будет обоснован).

Так как и f(x) – непрерывны в замкнутых областях, то они ограничены:

Поэтому:

Значит ряд (9) мажорируется рядом

- (11)

геометрический ряд – сходится, если , то есть при

(12)

Вывод: если имеет место (12), то ряд (9) сходится равномерно и абсолютно.

Замечания:

Решение линейного интегрального уравнения (1) было получено тремя различными методами и притом в трех различных формах. Приведенный метод – метод последовательных подстановок – был развит Нейманом, Лиувиллем и Вольтерра. Этот метод дает решение в виде степенного ряда относительно λ, причем коэффициенты при различных степенях λ являются функциями от х. Ряд сходится при λ, меньших по абсолютной величине, чем некоторое число (при малых λ). Этот метод называют еще «методом малого параметра».

Покажем теперь, что уравнение Фредгольма не может иметь более одного решения в классе ограниченных функций, если λ удовлетворяет неравенству (12).

Пусть y(x) и y*(x) – два ограниченных решения уравнения, тогда разность ω(x)=y(x)-y*(x) ограничена:

,

то есть является решением однородного уравнения.

Имеем

, где при a≤x, ξ≤b.

Далее

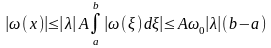
Заменяя в интеграле , получим

и т.д.

После «k» шагов:

,

но так как , то и, следовательно, , где ε>0 – любое число, => ω(x)=0 => y(x)=y*(x).

Замечание:

Значит, в круге нет собственных значений ядра.

Тема 2 Метод последовательных приближений (метод итераций) для уравнения Фредгольма II рода

Было доказано существование и единственность непрерывного решения при условии, что ядро уравнения , свободный член уравнения непрерывны, а параметр λ удовлетворяет неравенству (12). Докажем этот результат при более общих предположениях на ядро уравнения (1).

Покажем, что если

(13)

то существует единственное решение уравнения Фредгольма (1) при

, где (14)

(15)

Доказательство: Для интегрального уравнения

построим последовательность приближений

Аналогично,

………………………………………………………………………………..

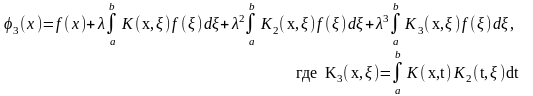
, где (16)

(17)

Функция называется «k»-тым итерированным ядром по отношению к данному ядру.

Итерированные ядра удовлетворяют следующему соотношению:

(18)

Допустим, что последовательные приближения (16) сходятся. Перейдем к пределу в (16) при n→∞:

(19)

Мы получим решение (19) уравнения (1) в виде ряда. Докажем, что этот ряд является сходящимся.

Пусть

(следует из (13)). Имеем

По неравенству Буняковского - Шварца (неравенство Гельдера для интегралов)

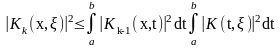
Проинтегрируем неравенство по ξ:

Отсюда для верхних граней интегралов выполняется соотношение:

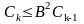(k=1,2,…)

Отсюда

В (19) общий член ряда оценивается следующим образом:

, то есть

, где (20)

Рассмотрим мажорантный геометрический ряд

Он сходится, если В|λ|<1, то есть при . Значит, ряд в формуле (19) равномерно и абсолютно сходится при

Формула (19) определяет единственное решение уравнения (1).

Докажем единственность решения:

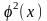Допустим противное: существует два решения и , то есть

Вычитая почленно и обозначая - =ω(х), получим:

(21)

Или (22)

Проинтегрируем неравенство по х:

Или

Но так как , то >0 => ≤0 => =0

Но тогда из (22): ≤0 => ω(x)=0 или = при x [a,b].

Теорема доказана.

Замечания:

На практике метод последовательных приближений (метод итераций) может дать только приближенное решение интегрального уравнения, так как ряды, как правило, не суммируются, в конечном счете. В тех случаях, когда сумму ряда в формуле (19) можно найти без труда, оказывается возможным с помощью того или иного специального приема решить интегральное уравнение, не прибегая к наложенной выше теории.

2) Условия теоремы достаточные, но не необходимые. Решение может существовать и при , но оно не может быть найдено методом приближенных вычислений. В этом случае применяются другие методы решения уравнений.

Вывод: если имеет место (12), то ряд (9) сходится равномерно и абсолютно.

Пример:

Рассмотрим уравнение:

где

Здесь 0,1

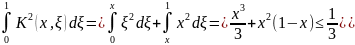
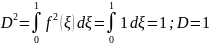
Итак, последовательные приближения сходятся. Если в ряде (5) §2 ограничиться «n» членами, то ошибка не превосходит величины – сумма б. убыв. геометрической прогрессии, начиная с «n+1» - члена прогрессии.

Найдем приближенное решение, ограничиваясь тремя: приближениями. При этом мы оставляем в ряде три члена, а ошибка не превосходит

Если взять два приближения:

Имеем последовательные приближения:

Если мы положим , то погрешность не будет превосходить 0,0001.

Подробнее: