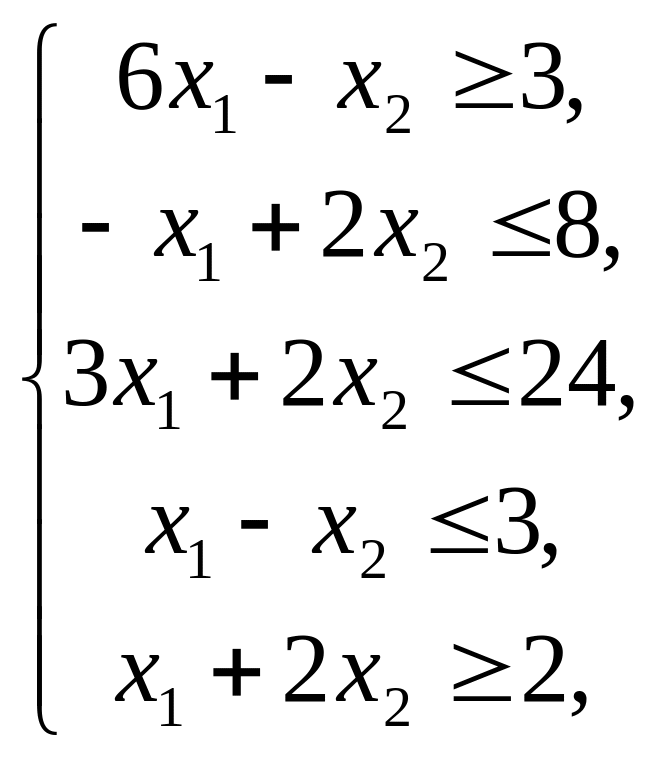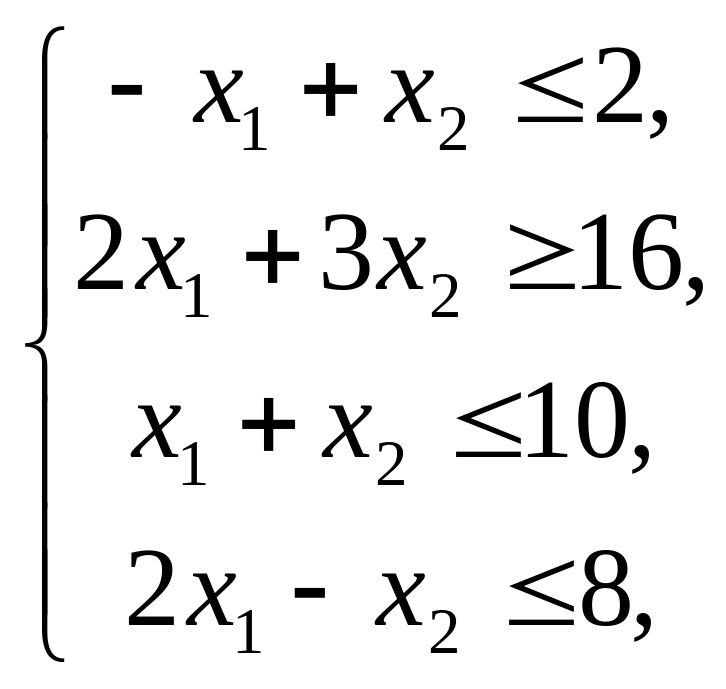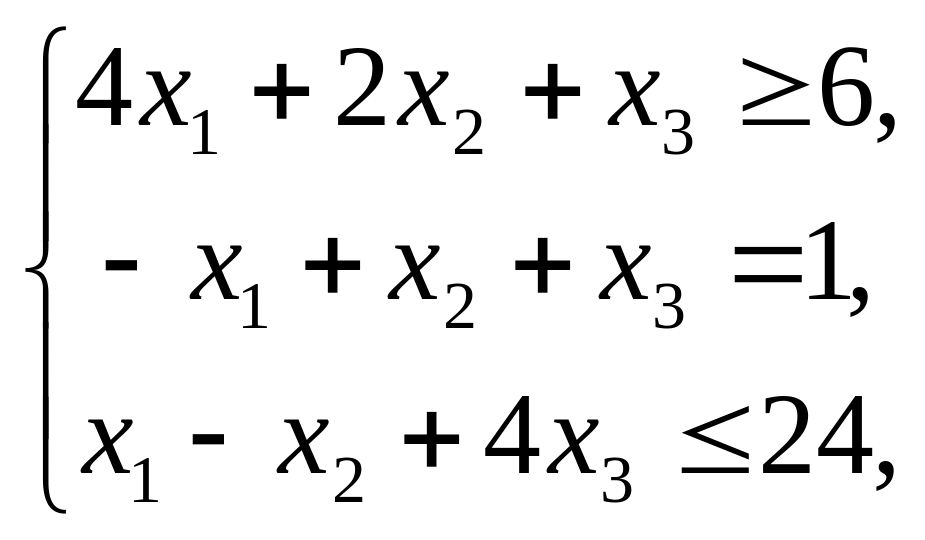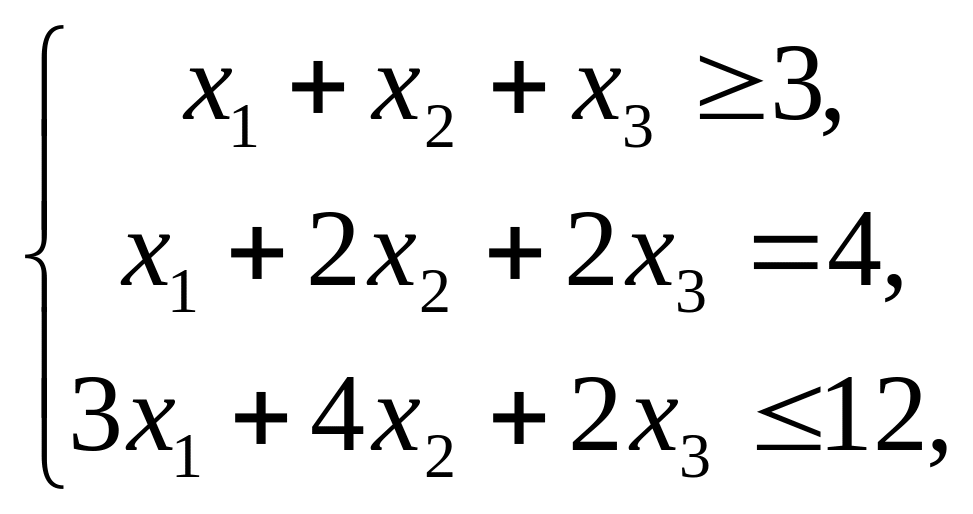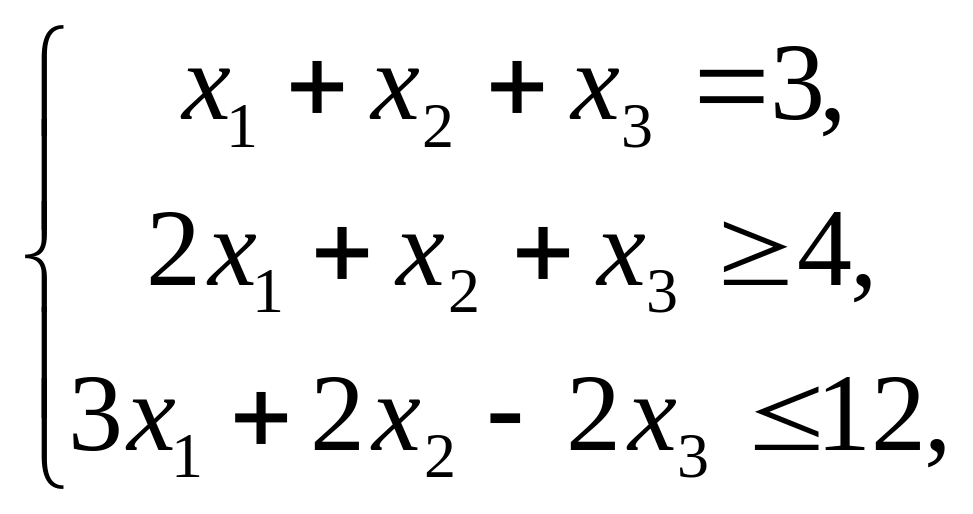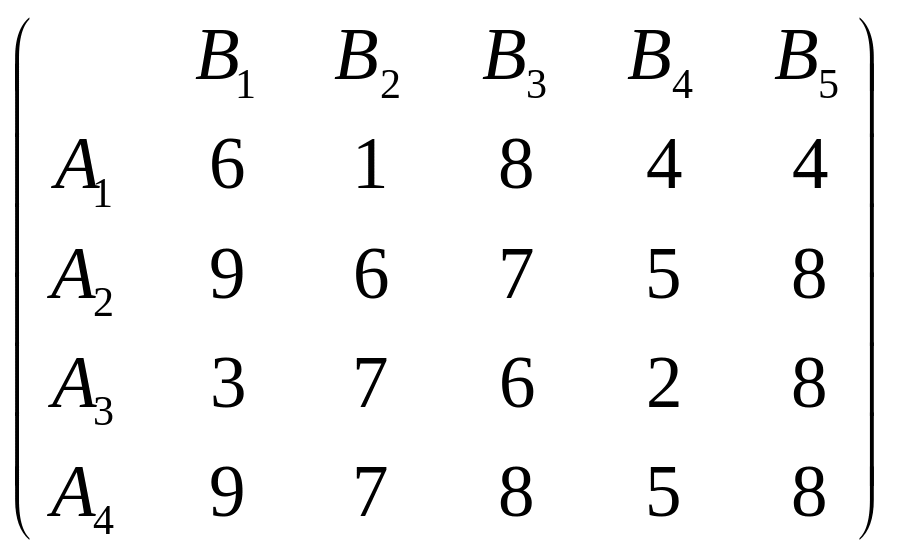Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Горно-Алтайский государственный университет»
Кафедра экономики предприятия и прикладной информатики
Расчтно-графическая работа
Индивидуальная работа студента (ИРС)
Перечень компетенций (части компетенций), проверяемых оценочным средством:
ПК-17 способен применять методы анализа прикладной области на концептуальном, логическом, математическом и алгоритмическом уровнях
ПК-21 способен применять системный подход и математические методы в формализации решения прикладных задач
Теоретические основы оптимизации
Задание 1. Задачи без ограничений
z = x2 + xy + y2 – 3ax – 3by.
z = x3y2 (a – x – y).
z = x4 + y4 – 2x2 + 4xy – 2y2.
z = x2 – xy + y2 + 3x – 2y +1.
z = x2 + xy + y2 +
 +
+
 ,
x
> 0, y
> 0.
,
x
> 0, y
> 0.z = x3 + y3 – 3axy.
z = xy2 – xy – xy3, x > 0, y > 0.
z = y
 - y2
– x
+ 6y.
- y2
– x
+ 6y.z = 4 -
 .
.
Задание 2. Задачи с ограничениями типа равенств
z = x2 + y2 – xy + x + y – 4; x + y +3 = 0.
z =
 ; x
+ y
= 2.
; x
+ y
= 2.z = x + y;
 .
.z = x · y; x2 + y2 = 1.
z = x y2; x + 2y = 1.
z = x + 2y; x2 + y2 = 1.
z = x y; x2 + y2 = 2a2.
z = xm + ym (m > 1); x + y = 2 (x ≥ 0, y ≥ 0).
z = a cos2x + b cos2y; y – x =
 .
.z = ; .
Задание 3. Задачи с ограничениями типа равенств и неравенств
z = x2 + y2 – xy + x + y – 4; x + y +3 = 0; ;
 .
.z = ; x + y = 2; y – x ≥ .;.
z = x + y; ; x + y ≤ 2 (x ≥ 0, y ≥ 0);.
z = x y; x2 + y2 = 1; x2 + y2 < 2a2.
z = x y2; x + 2y = 1; x2 + y2 > 1.
z = x + 2y; x2 + y2 = 1; x + 2y < 1.
z = x y; x2 + y2 = 2a2.; x2 + y2 ≤ 1
z = xm + ym (m > 1); x + y = 2 (x ≥ 0, y ≥ 0); .
z = a cos2x + b cos2y; y – x = .; x + y ≤ 2
z = ; ; x + y +3 ≤ 0.
Задание 4. Решите задачи
1.Определить
наибольшую вместимость цилиндрического
ведерка, поверхность которого (без
крышки) равна S.
Ответ:
![]() .
.
2. Определить
наибольшую вместимость конической
воронки, поверхность которой равна S.
Ответ:
![]() .
.
3. Определить
наибольшую вместимость цилиндрической
ванны с полукруглым поперечным сечением,
если поверхность ванны равна S.
Ответ:
![]() .
.
4. Найти наибольший
объем тела, образованного вращением
треугольника с периметром р
вокруг одной из его сторон. Ответ:
![]() .
.
5. Найти наименьшую
поверхность, которую может иметь
прямоугольный параллелепипед, если его
объем равен V.
Ответ:
![]() .
.
6. Определить
наименьшее количество материала,
необходимого для изготовления шатра
заданного объема V,
имеющего форму цилиндра с конической
крышкой. Ответ:
![]() .
.
7. В полушар радиуса
R
вписать прямоугольный параллелепипед
наибольшего объема. Ответ: измерения
параллелепипеда
![]() ,
,
,
,
![]() .
.
8. В данный прямой
конус вписать прямоугольный параллелепипед
наибольшего объема. Ответ: высота
параллелепипеда равна
![]() высоты конуса.
высоты конуса.
9. Найти кратчайшее
расстояние между параболой y=x2
и прямой x-y-2=0.
Ответ:
![]() .
.
10. Найти кратчайшее
расстояние от точки М(1, 0) до эллипса
4x2+9y2=36.
Ответ:
![]() .
.
Линейное программирование (задачи должны быть решены аналитически и в программе ms Excel)
Решить графическим методом задачи с двумя переменными (табл. 1).
Решить графическим методом задачи с n переменными (табл. 2).
Решить методом искусственного базиса задачи линейного программирования (см. табл. 2).
Решить симплексным методом задачи (табл. 3).
Решить методом потенциалов транспортные задачи (табл. 4).
Таблица 1. Варианты задания 1
Вариант |
Задача |
Вариант |
Задача |
1 |
Z(X) = 2x1 + 4x2 → max,
x1 ≥ 0, x2 ≥ 0 |
6 |
Z(X) = -3x1 - x2 → min,
x1 ≥ 0, x2 ≥ 0 |
2 |
Z(X) = 15x1 + 10x2 → max,
x1 ≥ 0, x2 ≥ 0 |
7 |
Z(X) = 2x1 + 3x2 → max,
x1 ≥ 0, x2 ≥ 0 |
3 |
Z(X) = 3x1 + 2x2 → max,
x1 ≥ 0, x2 ≥ 0 |
8 |
Z(X) = 4x1 + 6x2 → max,
|
4 |
Z(X) = 2x1 + 5x2 → min,
x1 ≥ 0, x2 ≥ 0 |
9 |
Z(X) = - x1 + 4x2 → min,
x2 ≥ 0 |
5 |
Z(X) = 2x1 - 4x2 → max,
x1 ≥ 0, x2 ≥ 0 |
10 |
Z(X) = x1 + 4x2 → min,
x1 ≥ 0, x2 ≥ 0 |
Таблица 2. Варианты заданий 2 и 3
Вариант |
Задача |
Вариант |
Задача |
1 |
Z(x) = 2x1 + 8x2 + 3x3 + 4x4 → min,
xj ≥ 0, j = 1, 2, 3, 4 |
6 |
Z(x) = 2x1 + 6x2 + x3 + x4 → max,
xj ≥ 0, j = 1, 2, 3, 4 |
2 |
Z(x) = 2x1 + 3x2 - x3 + 4x4 → min,
xj ≥ 0, j = 1, 2, 3, 4 |
7 |
Z(x) = 2x1 + 5x2 + x3 + x4 → max,
xj ≥ 0, j = 1, 2, 3, 4 |
3 |
Z(x) = 4x1 + 13x2 + 3x3 + 6x4 → min,
xj ≥ 0, j = 1, 2, 3, 4 |
8 |
Z(x) = 9x1 + 2x2 + 4x3 - 8x4 → max,
xj ≥ 0, j = 1, 2, 3, 4 |
4 |
Z(x) = x1 + x2 + 3x3 + 4x4 → min,
xj ≥ 0, j = 1, 2, 3, 4 |
9 |
Z(x) = x1 - 2x2 - x3 + 3x4 → max,
xj ≥ 0, j = 1, 2, 3, 4 |
5 |
Z(x) = 11x2 + x3 - 4x4 → min,
xj ≥ 0, j = 1, 2, 3, 4 |
10 |
Z(x) = 2x1 + x2 - x3 - 2x4 → min,
xj ≥ 0, j = 1, 2, 3, 4 |
Таблица 3. Варианты задания 4
Вариант |
Задача |
Вариант |
Задача |
1 |
Z(x) = x1 + 4x2 + x3 → max,
xj ≥0, j=1, 2, 3 |
6 |
Z(x) = -2x1 - 2x2 - 2x3 → min,
xj ≥0, j=1, 2, 3 |
2 |
Z(x) = 2x1 + x2 - x3 → min,
xj ≥0, j=1, 2, 3 |
7 |
Z(x) = -3x1 - 2x2 - 2x3 → min,
xj ≥0, j=1, 2, 3 |
3 |
Z(x) = x1 - x2 + x3 → max,
xj ≥0, j=1, 2, 3 |
8 |
Z(x) = -2x1 + 8x2 + 3x3 → min,
xj ≥0, j=1, 2, 3 |
4 |
Z(x) = 5x1 + 2x2 + x3 → max,
xj ≥0, j=1, 2, 3 |
9 |
Z(x) = 6x1 + 7x2 + 9x3 → min,
xj ≥0, j=1, 2, 3 |
5 |
Z(x) = x1 - 8x2 - 3x3 → max,
xj ≥0, j=1, 2, 3 |
10 |
Z(x) = 5x1 + 2x2 + x3 → max,
xj ≥0, j=1, 2, 3 |
Таблица 4. Варианты задания 5
Вариант |
Задача |
|
Вариант |
Задача |
||||||||||
1 |
bj ai |
10 |
10 |
25 |
25 |
30 |
|
6 |
bj ai |
50 |
50 |
100 |
100 |
50 |
10 |
1 |
5 |
7 |
9 |
3 |
|
50 |
3 |
4 |
6 |
5 |
13 |
||
20 |
4 |
6 |
4 |
7 |
13 |
|
50 |
6 |
3 |
7 |
6 |
10 |
||
10 |
1 |
5 |
3 |
4 |
9 |
|
100 |
10 |
5 |
2 |
2 |
6 |
||
30 |
2 |
4 |
2 |
10 |
3 |
|
150 |
9 |
4 |
4 |
9 |
5 |
||
10 |
3 |
2 |
5 |
6 |
4 |
|
100 |
3 |
2 |
4 |
2 |
3 |
||
2 |
bj ai |
100 |
200 |
200 |
300 |
200 |
|
7 |
bj ai |
200 |
200 |
400 |
200 |
100 |
100 |
4 |
3 |
5 |
2 |
3 |
|
200 |
5 |
2 |
1 |
6 |
4 |
||
200 |
7 |
1 |
2 |
3 |
1 |
|
300 |
6 |
2 |
4 |
4 |
6 |
||
300 |
9 |
2 |
4 |
5 |
6 |
|
200 |
9 |
2 |
3 |
7 |
5 |
||
100 |
1 |
3 |
6 |
4 |
10 |
|
200 |
7 |
3 |
5 |
8 |
7 |
||
200 |
5 |
8 |
15 |
6 |
15 |
|
100 |
3 |
2 |
4 |
2 |
3 |
||
3 |
bj ai |
200 |
400 |
100 |
200 |
100 |
|
8 |
bj ai |
100 |
150 |
150 |
100 |
300 |
200 |
1 |
7 |
12 |
2 |
5 |
|
50 |
3 |
4 |
5 |
4 |
1 |
||
100 |
2 |
3 |
8 |
4 |
7 |
|
100 |
1 |
2 |
7 |
1 |
5 |
||
200 |
3 |
5 |
4 |
6 |
9 |
|
150 |
4 |
6 |
6 |
3 |
7 |
||
400 |
4 |
4 |
3 |
8 |
2 |
|
100 |
2 |
7 |
4 |
7 |
2 |
||
400 |
5 |
3 |
7 |
10 |
1 |
|
200 |
3 |
8 |
9 |
4 |
5 |
||
4 |
bj ai |
5 |
10 |
15 |
15 |
15 |
|
9 |
bj ai |
400 |
600 |
500 |
400 |
500 |
10 |
2 |
5 |
5 |
6 |
7 |
|
400 |
1 |
2 |
3 |
1 |
2 |
||
5 |
4 |
3 |
4 |
4 |
3 |
|
500 |
3 |
4 |
2 |
4 |
5 |
||
5 |
5 |
2 |
3 |
6 |
2 |
|
600 |
5 |
7 |
6 |
3 |
9 |
||
10 |
3 |
6 |
5 |
7 |
8 |
|
400 |
4 |
10 |
15 |
4 |
8 |
||
15 |
1 |
9 |
7 |
6 |
4 |
|
200 |
3 |
4 |
5 |
3 |
7 |
||
5 |
bj ai |
10 |
30 |
30 |
30 |
40 |
|
10 |
bj ai |
100 |
150 |
150 |
100 |
100 |
10 |
3 |
1 |
3 |
4 |
3 |
|
50 |
3 |
4 |
5 |
4 |
6 |
||
30 |
5 |
1 |
2 |
2 |
6 |
|
100 |
1 |
5 |
7 |
1 |
5 |
||
60 |
2 |
3 |
4 |
1 |
1 |
|
150 |
4 |
6 |
6 |
3 |
4 |
||
10 |
6 |
2 |
5 |
3 |
2 |
|
100 |
2 |
7 |
4 |
7 |
2 |
||
60 |
3 |
7 |
4 |
4 |
1 |
|
100 |
1 |
9 |
6 |
3 |
2 |
||
Специальные методы оптимизации
Задача 1. Теория игр. Игра в чистых стратегиях
1. Найти решение и цену игры, заданной следующей платежной
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
Задача 2. Теория игр (задачу решить аналитически и графически)
Найти решение и цену игры, заданной следующей платежной матрицей:
1 |
|
2. |
|
3. |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
Задача 3. Принятие решений в условиях недостатка информации
Вариант 1
Молодой российский бизнесмен предполагает построить ночную дискотеку неподалеку от университета. По одному из допустимых проектов предприниматель может в дневное время открыть в здании дискотеки столовую для студентов. Другой вариант не связан с дневным обслуживанием клиентов. Представленные бизнес-планы показывают, что план, связанный со столовой, может принести доход в 250 тыс. рублей. Без открытия столовой бизнесмен может заработать 175 тыс. рублей Потери в случае открытия дискотеки со столовой составят 55 тыс. рублей, а без столовой - 20 тыс. рублей Определите наиболее эффективную альтернативу на основе средней стоимостной ценности в качестве критерия. Вероятность наступления благоприятного состояния равен 0,5; неблагоприятного – 0,5.