7.4 Обработка результатов прямых измерений

При прямом измерении некоторой физической вели­чины А выполняются следующие действия:

а) Производят измерение физической величины n раз (А₁, А_{2 ….} А_n )..

б) Находят среднее значение измеряемой величины

в) Находят абсолютные погрешности Δ А _i по формуле

каждого измерения и среднюю абсолютную погрешность всей се­рии измерений:

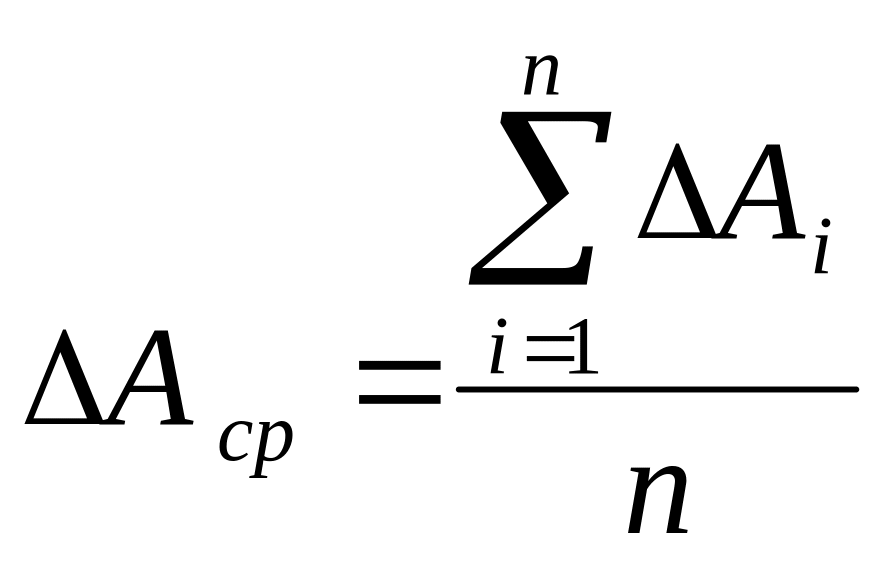
г) Записывая результат измерения в виде в качестве абсолютной погрешности результата ΔА бе­рут либо среднюю абсолютную погрешность, либо при­борную погрешность (в зависимости от того, какая из этих погрешностей больше).

д) Абсолютная погрешность результата округляется до одной значащей цифры, а среднее значение измеряе­мой величины округляется или уточняется до разряда, оставшегося в абсолютной погрешности после округления.

е) Подсчитывается относительная погрешность ре­зультата:

Пример [1]. Измерение диаметра d шарика производи­лось пять раз с помощью микрометра, абсолютная по­грешность которого равна ΔD _приб = ±0,01 мм. Резуль­таты измерения диаметра шарика: d₁ = 5,27 мм, d₂ = 5,30 мм» d₃ = 5,28 мм, d₄ — 5,32 мм, d₅ = 5,28 мм.

Среднее значение диаметра шарика:

Абсолютные погрешности измерений равны: Δd ₁ = 0,02 мм, Δd ₂ = 0,01 мм, Δd ₃ = 0,01 мм, Δd ₄ — 0,03 мм, Δd ₅ = 0,01 мм, а средняя абсолютная погрешность

Поскольку средняя абсолютная погрешность больше приборной, результат измерения равен d = (5,29 ± 0,02) мм.

Относительная погрешность измерения диаметра ша­рика составляет

7.5 Обработка результатов косвенных измерений

Пусть физическая величина А связана с несколькими другими величинами А₁, А_{2 ….} А _k некоторой функцио­нальной зависимостью:

A = f (A₁, A₂, … A _k)

Среди величин A₁, A₂, … A _k могут содержаться непо­средственно измеряемые величины А _пi, табличные вели­чины A _{т i} (значения которых в данном опыте не изме­ряются, а берутся из таблиц) и так называемые данные установки A_Yi (некоторые известные заранее характе­ристики экспериментальной установки, не измеряемые в данном опыте).

В результате обработки всех непосредственно изме­ряемых величин A _пi для каждой из них оказы­ваются найденными: среднее значение (А _пi )_ср, абсолют­ная погрешность ΔА _пi и относительная погрешность E_пi.

Результат для косвенно измеряемой величины А в простейших случаях получают по следующей схеме:

а) Среднее значение А_ср подсчитывают по средним значениям величин, от которых зависит измеряемая ве­личина А:

А_ср = f (А_{1 ср}, А_{2 ср}, … А _{k ср})

б) По виду функциональной зависимости величины А от непосредственно измеряемых, и.табличных вели­чин, а также от данных установки рассчитывается относительная погрешность Е. В случае простейших функ­циональных зависимостей формула для расчета относительной погрешности Е обычно имеет вид

E = c₁ E₁ + c₂E₂ + … + c_kE_k

Где c₁, c₂, c _k — целочисленные или дробные безраз­мерные коэффициенты, а Е₁, Е₂, ..., E _k — относитель­ные погрешности измерения величин A₁, A₂, … A _k .

В таблице 3 приведены формулы для расчета относительных Е и абсолютных ΔА погрешностей кос­венно измеряемой величины, когда последняя свя­зана с другими величинами наиболее простыми и часто встречающимися в технических задачах функциональными зависимостями.

Табличные величины берутся с такой точностью, чтобы их относительные погрешности были меньше остальных относительных погрешностей, содержащихся в предыдущей формуле.

Если значения данных установки не записаны в об­щепринятой форме, то обычно считается, что они измерены с точностью, равной половине последнего указанного разряда.

в) По среднему значению измеряемой величины А _ср и относительной погрешности Е подсчитывают абсолют­ную погрешность результата ΔА:

причем ее округляют так, чтобы она содержала лишь одну значащую цифру.

г) Окончательный результат измерения представ­ляют в виде

при этом среднее значение А _ср округляют или уточняют до разряда, оставшегося в значении абсолютной по­грешности ΔА после его округления.

Пример 1. Определить плотность некоторого однородного тела по результатам непосредственно произведенных измерений его массы m и объема V; m = (25,4 ± 0,5) -10 ^{- 3} кг, V = (2,94 ± 0,05) • 10 ^-6 м³ Среднее значение плотности тела равно

Относительная погрешность измерения плотности Е_ρ равна сумме относительных погрешностей измерения массы Е_m и объема E_v

Абсолютная погрешность измерения плотности Δρ равна

Δρ = ρ_ср Е_ρ = 8,65 ^. 10^{3 .} 0,04 ≈ 0,3 10 ³ кг/м³.

Округляя значение ρ_ср, окончательный результат запи­шем в виде

ρ = (8,6 ±0,3) ^. 10³ кг/м³.

Пример 2 [1]. Определить объем V цилиндра по ре­зультатам прямых измерений его диаметра d и высоты h:

d = (3,46 ± 0,04) ^. 10 ^{- 2} А = (4,87 ± 0,05) 10^-2 м.

Прежде чем рассчитать среднее значение объема цилиндра по формуле

оценим, с какой точностью должна быть взята из таблицы величина π (например, мы располагаем таблич­ным значением π = 3,141593).

Относительная погрешность результата E_v в данном случае равна (см. таблицу 4). Е_v = E_π + 2E_d +E_h

где

т.е. Е_v = E_π + 0,03

Чтобы неточность значения числа π заметно не ухудшила результата измерения, должно быть Е_π <0,01. Если, например, взять число π с точностью до десятых, то

и относительная погрешность результата составит Ev = 0,04. Если же взять число π с точностью до сотых, то

и E_v = 0,003

Следовательно, в данном случае без ущерба для точности результата можно принять π = 3,14. Тогда

7.6 Приближенные вычисления без точного учета погрешностей

Производя обработку многочисленных измерений, часто не подсчитывают погрешности отдельных резуль­татов и судят о погрешности приближенного значения величины (числа), указывая количество верхних знача­щих цифр в этом числе.

Нули, стоящие в числе слева, значащими цифрами не считаются. Нули в середине или в конце числа (справа), обозначающие отсутствие в числе единиц соответствую­щих разрядов, - значащие цифры. Например, в числе 0,08040 первые два нуля - незначащие, а третий и чет­вертый - значащие.

Нули, поставленные в конце целого числа взамен не­известных цифр и служащие лишь для определения разрядов остальных цифр, значащими не считаются. В по­добных случаях нули в конце числа лучше не писать и заменять их соответствующей степенью числа 10, На­пример, если число 4200 измерено с абсолютной погреш­ностью ±100, то это число должно быть записано в виде 42^.10² или 4,2-10³. Такая запись подчеркивает, что в данном числе содержатся лишь две значащие цифры.

Если приближенное значение величины содержит лишние или недостоверные цифры, то его округляют, сохраняя только верные значащие цифры и отбрасывая лишние. При этом руководствуются следующими пра­вилами округления:

а) Если первая отбрасываемая цифра больше 5, то последняя сохраняемая цифра увеличивается на единицу. Например, округляя число 27,3763 до сотых, сле­дует записать 27,38.

б) Если первая отбрасываемая цифра меньше 5 или равна 5, то последняя сохраняемая цифра не изме­няется. Например, округляя число 13 847 до сотен, за­писывают 138 ^.10².

в) Если отбрасываемая часть числа состоит из одной цифры 5, то число округляют так, чтобы последняя со­храняемая цифра была четной. Например, при округлении до десятых 23,65 ≈ 23,6, но 17,76 ≈ 17,8.

Производя различные математические действия с приближенными числами, руководствуются следую­щими правилами подсчета цифр:

а) При сложении и вычитании в результате сохра­няют столько десятичных знаков, сколько их со­держится в числе с наименьшим количеством десятич­ных знаков.

б) При умножении и делении в результате сохра­няют столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр.

Исключения из этого правила допускаются в тех слу­чаях, когда один из сомножителей произведения начи­нается с единицы, а сомножитель, содержащий наимень­шее количество значащих цифр, - с какой-нибудь дру­гой цифры. В этих случаях в результате сохраняют на одну цифру больше, чем в числе с наименьшим количе­ством значащих цифр.

в) Результат расчета значений функций

некоторого приближенного числа х должен содер­жать столько значащих цифр, сколько их имеется в числе х.

Если некоторые приближенные числа содержат больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня и т. д.), чем другие, то их предварительно округляют, сохраняя только одну лишнюю цифру [1].

Цель работы;

Определение относительной и абсолютной погрешности измерения при работе насосов, гидроприводов и гидропередач. Вид лабораторной установки представлен на рисунках 1-6.

Порядок выполнения работы:

Включить установку (лабораторные работы по гидравлике работы 2.1-2.6) вид установки (номер лабораторной работы указывается преподавателем в карточке задания к лабораторной работе). Установить необходимые параметры работы (указанны в задании). Провести ряд опытов (6-8), при одних и тех же основных параметров установки указанных в задании. Записать результаты в таблицу (выдается с заданием). Провести вычисления относительной и абсолютной погрешности результатов измерений по каждому из приборов установки.

Представление результатов работы:

Результаты работы представляются на стандартных листах размером А-4. Приводится схема установки и ее описание. Описание приборов установки, Основные формулы. Ход вычисления и выводы по работе. На рисунке (для примера) представлен вид установки 1.

Рисунок к лабораторной работе 1

Классификация погрешности измерения

Погрешности измерений

По форме числового выражения

По закономерностям проявления

Абсолютные

Предельные

Случайные

Систематические

Грубые промахи

Относительные

По виду

источника

По характеру проявления

Приведённые

Средние квадратические (стандартные)

Методические

Переменные

Постоянные

Вероятные

Прогрессирующие

Условно постоянные

Средние

Инструментальные

Периодические

Изменяющиеся по сложному закону

Средние арифметические

Безусловно постоянные

Субъективные